第五章 曲线运动复习课(共24张ppt)
文档属性
| 名称 | 第五章 曲线运动复习课(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 648.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-05 10:55:28 | ||
图片预览







文档简介
课件24张PPT。复习课第五章曲线运动一、复习目标:
1.本章知识网络构建。
2. 平抛运动规律的应用及运动的合成与分解。
3. 表述圆周运动的物理量和竖直平面内的圆周运动,临界问题。
4. 会利用学过的圆周运动知识处理生活中的圆周运动问题。
二、重点、难点:
重点:平抛运动和圆周运动规律的实际应用。
难点:竖直平面内的圆周运动问题。
三、考点分析:
平抛运动有时与电场力结合进行综合考查,圆周运动有时与洛伦兹力和天体运动结合进行综合考查,竖直平面内的圆周运动问题是近几年的高考热点,考查难度较大。本章知识的考查会涉及与实际相联系的题。考查内容见下表:一、曲线运动中的绳、杆关联问题
1.绳、杆关联问题特点:绳、杆等有长度的物体,在运动过程中,其两端点的速度通常是不一样的,但两端点的速度是有联系的,称之为“关联”速度。关联速度的关系——沿杆(或绳)方向的速度分量大小相等。2.常用的解题思路和方法:
(1)先确定合运动的方向,即物体实际运动的方向;
(2)然后分析这个合运动所产生的实际效果(一方面使绳或杆伸缩的效果,另一方面使绳或杆转动的效果)以确定两个分速度的方向(沿绳或杆方向的分速度和垂直绳或杆方向的分速度);
(3)作出速度分解的示意图,即根据平行四边形定则,作出合速度与分速度的平行四边形;
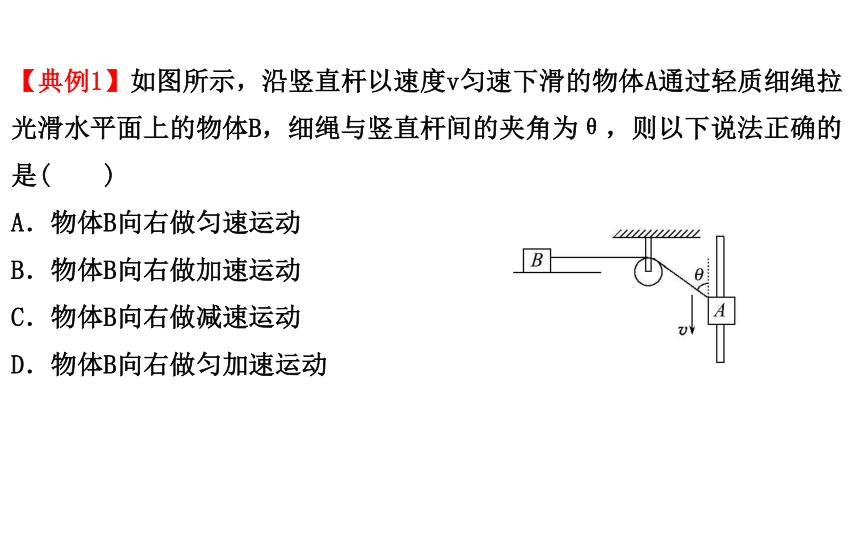
(4)利用三角形、三角函数等数学知识求解。【典例1】如图所示,沿竖直杆以速度v匀速下滑的物体A通过轻质细绳拉光滑水平面上的物体B,细绳与竖直杆间的夹角为θ,则以下说法正确的是( )
A.物体B向右做匀速运动
B.物体B向右做加速运动
C.物体B向右做减速运动
D.物体B向右做匀加速运动【标准解答】选B。A、B物体沿细绳方向的速度分别为vAcosθ
和vB,故vB=vAcosθ=vcosθ,vB逐渐增大,A、C错,B对;由
vB=vcosθ和cosθ= (d为滑轮到竖直杆的水平距离)
可知,cosθ不是均匀变化的,所以B不是做匀加速运动,故D
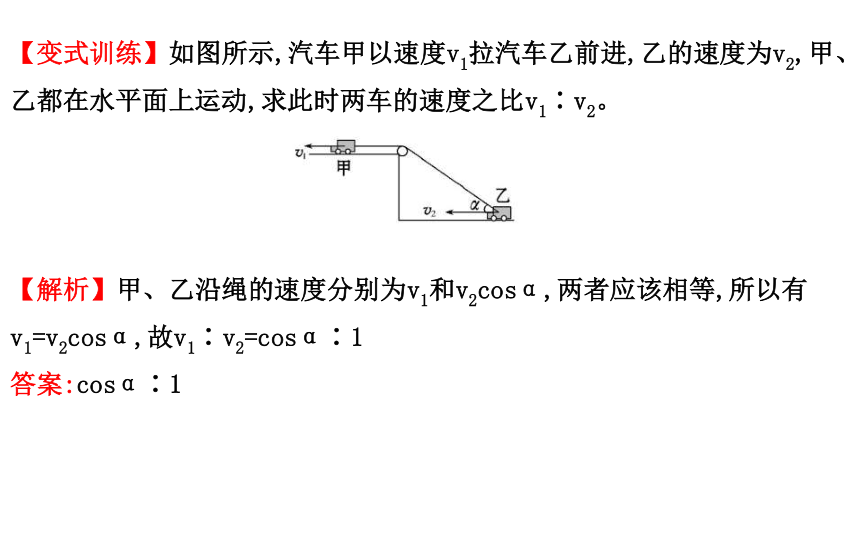
错。【变式训练】如图所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求此时两车的速度之比v1∶v2。
【解析】甲、乙沿绳的速度分别为v1和v2cosα,两者应该相等,所以有v1=v2cosα,故v1∶v2=cosα∶1
答案:cosα∶1二、平抛运动的特征和解题方法
平抛运动是典型的匀变速曲线运动,它的动力学特征是:水平方向有初速度而不受外力,竖直方向只受重力而无初速度,抓住了平抛运动的这个初始条件,也就抓住了它的解题关键,现将常见的几种解题方法介绍如下:
1.利用平抛运动的时间特点解题:平抛运动可分解成水平方向的匀速直线运动和竖直方向的自由落体运动,只要抛出的时间相同,下落的高度和竖直分速度就相同。2.利用平抛运动的偏转角解题:设做平抛运动的物体,下落高度为h,水平位移为x时,速度vA与初速度v0的夹角为θ,由图可得:tanθ= ①
将vA反向延长与x相交于O点,设A′O=d,
则有:tanθ=
解得d= tanθ= =2tanα ②
①②两式揭示了偏转角和其他各物理量的关系。3.利用平抛运动的轨迹解题:平抛运动的轨迹
是一条抛物线,已知抛物线上的任意一段,就
可求出水平初速度和抛出点,其他物理量也就
迎刃而解了。设图为某小球做平抛运动的一段
轨迹,在轨迹上任取两点A和B,过A点作竖直线,过B点作水平线相交于C点,然后过BC的中点D作垂线交轨迹于E点,再过E点作水平线交AC于F点,小球经过AE和EB的时间相等,设为单位时间T。由Δy=gT2知【典例2】在运动的合成与分解的实验中,红蜡块在长1 m的玻璃管中竖直方向能做匀速直线运动,现在某同学拿着玻璃管沿水平方向做匀加速直线运动,并每隔一秒画出了蜡块运动所到达的位置如图所示,若取轨迹上的C(x,y)点作该曲线的切线(图中虚线)交y轴于A点,则A点的坐标为( )
A.(0,0.6y)
B.(0,0.5y)
C.(0,0.4y)
D.不能确定【标准解答】选B。红蜡块的运动可看作类平抛运动,则图像
的切线与竖直方向的夹角的正切值tanα= 连接OC可得直
线OC与y轴的夹角为tanθ= 所以tanθ=
即A点为竖直方向上位移的中点,所以A点的坐标为(0,0.5y),
B正确。【变式训练】在同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图所示,不计空气阻力。要使两球在空中相遇,则必须( )
A.先抛出A球
B.先抛出B球
C.同时抛出两球
D.A球的初速度大于B球的初速度【解析】选C、D。两球从同一高度抛出且能在空中相遇,表明它们被同时抛出,A、B错,C对。相同时间内,A球的水平位移较大,由x=v0t知A球的初速度较大,D对。三、圆周运动中的临界问题
1.临界状态:当物体从某种特性变化为另一种特性时发生质的飞跃的转折状态,通常叫做临界状态,出现临界状态时,既可理解为“恰好出现”,也可理解为“恰好不出现”。常见的类型有轻绳、轻杆牵引小球在竖直面内做圆周运动的条件,汽车过拱桥、摩擦力作用下物体在水平面内做圆周运动的条件。2.轻绳类:轻绳拴球在竖直面内做圆周运动,过最高点时,临界
速度为 此时F绳=0。
3.轻杆类:
(1)小球能过最高点的临界条件:v=0,F=mg,F为支持力;
(2)当0 F ,F为支持力;
(3)当v= 时,F=0 ;
(4)当v> 时,F随v增大而增大, F为拉力。4.汽车过拱桥:如图所示,汽车过凸形桥顶时,
桥对车的支持力F=G- 由此式可以看出汽车
对桥的压力小于汽车的重力,而且是随着汽车
速度的增大而减小;
当压力为零时,即G- =0,v= 这个速度是汽车能正常
过拱桥的临界速度。
v < 是汽车安全过桥的条件。5.摩擦力提供向心力:如图所示,物体随着水平圆盘一起转
动,汽车在水平路面上转弯,它们做圆周运动的向心力等于静
摩擦力,当静摩擦力达到最大时,物体运动速度也达到最大,
由Fm= 得vm= 这就是物体以半径r做圆周运动的临界
速度。【典例3】如图所示,杆长为L,杆的一端固定一
质量为m的小球,杆的质量忽略不计,整个系统绕
杆的另一端O在竖直平面内做圆周运动,求:
(1)小球在最高点A时速度vA为多大时,才能使杆
对小球的作用力为零?
(2)如m=0.5kg,L=0.5m,vA=0.4m/s,g=10m/s2,则在最高点A时,杆对小球的作用力是多大?是推力还是拉力?【标准解答】(1) 若杆和小球之间相互作用力为零,那么小球
做圆周运动的向心力由重力mg提供,mg= 解得:vA=
(2)杆长L=0.5 m时,临界速度v临=
=2.2 m/s,vA=0.4 m/s解得:FA=mg- =(0.5×10- )N = 4.84 N
答案:(1) (2)4.84 N 推力【变式训练】如图所示,AB为半径为R的金属导轨(导轨厚度不计),a、b为分别沿导轨上、下两表面做圆周运动的小球(可看作质点),要使小球不致脱离导轨,则a、b在导轨最高点的速度va、vb应满足什么条件?【解析】对a球在最高点,由牛顿第二定律得:
mag-Na= ①
要使a球不脱离轨道,则Na>0 ②
由①②得:va<
对b球在最高点,由牛顿第二定律得:
mbg+Nb= ③
要使b球不脱离轨道,则Nb>0 ④
由③④得:vb>
答案:va< vb>
1.本章知识网络构建。
2. 平抛运动规律的应用及运动的合成与分解。
3. 表述圆周运动的物理量和竖直平面内的圆周运动,临界问题。
4. 会利用学过的圆周运动知识处理生活中的圆周运动问题。
二、重点、难点:
重点:平抛运动和圆周运动规律的实际应用。
难点:竖直平面内的圆周运动问题。
三、考点分析:
平抛运动有时与电场力结合进行综合考查,圆周运动有时与洛伦兹力和天体运动结合进行综合考查,竖直平面内的圆周运动问题是近几年的高考热点,考查难度较大。本章知识的考查会涉及与实际相联系的题。考查内容见下表:一、曲线运动中的绳、杆关联问题
1.绳、杆关联问题特点:绳、杆等有长度的物体,在运动过程中,其两端点的速度通常是不一样的,但两端点的速度是有联系的,称之为“关联”速度。关联速度的关系——沿杆(或绳)方向的速度分量大小相等。2.常用的解题思路和方法:
(1)先确定合运动的方向,即物体实际运动的方向;
(2)然后分析这个合运动所产生的实际效果(一方面使绳或杆伸缩的效果,另一方面使绳或杆转动的效果)以确定两个分速度的方向(沿绳或杆方向的分速度和垂直绳或杆方向的分速度);
(3)作出速度分解的示意图,即根据平行四边形定则,作出合速度与分速度的平行四边形;
(4)利用三角形、三角函数等数学知识求解。【典例1】如图所示,沿竖直杆以速度v匀速下滑的物体A通过轻质细绳拉光滑水平面上的物体B,细绳与竖直杆间的夹角为θ,则以下说法正确的是( )
A.物体B向右做匀速运动
B.物体B向右做加速运动
C.物体B向右做减速运动
D.物体B向右做匀加速运动【标准解答】选B。A、B物体沿细绳方向的速度分别为vAcosθ
和vB,故vB=vAcosθ=vcosθ,vB逐渐增大,A、C错,B对;由
vB=vcosθ和cosθ= (d为滑轮到竖直杆的水平距离)
可知,cosθ不是均匀变化的,所以B不是做匀加速运动,故D
错。【变式训练】如图所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求此时两车的速度之比v1∶v2。
【解析】甲、乙沿绳的速度分别为v1和v2cosα,两者应该相等,所以有v1=v2cosα,故v1∶v2=cosα∶1
答案:cosα∶1二、平抛运动的特征和解题方法
平抛运动是典型的匀变速曲线运动,它的动力学特征是:水平方向有初速度而不受外力,竖直方向只受重力而无初速度,抓住了平抛运动的这个初始条件,也就抓住了它的解题关键,现将常见的几种解题方法介绍如下:
1.利用平抛运动的时间特点解题:平抛运动可分解成水平方向的匀速直线运动和竖直方向的自由落体运动,只要抛出的时间相同,下落的高度和竖直分速度就相同。2.利用平抛运动的偏转角解题:设做平抛运动的物体,下落高度为h,水平位移为x时,速度vA与初速度v0的夹角为θ,由图可得:tanθ= ①
将vA反向延长与x相交于O点,设A′O=d,
则有:tanθ=
解得d= tanθ= =2tanα ②
①②两式揭示了偏转角和其他各物理量的关系。3.利用平抛运动的轨迹解题:平抛运动的轨迹
是一条抛物线,已知抛物线上的任意一段,就
可求出水平初速度和抛出点,其他物理量也就
迎刃而解了。设图为某小球做平抛运动的一段
轨迹,在轨迹上任取两点A和B,过A点作竖直线,过B点作水平线相交于C点,然后过BC的中点D作垂线交轨迹于E点,再过E点作水平线交AC于F点,小球经过AE和EB的时间相等,设为单位时间T。由Δy=gT2知【典例2】在运动的合成与分解的实验中,红蜡块在长1 m的玻璃管中竖直方向能做匀速直线运动,现在某同学拿着玻璃管沿水平方向做匀加速直线运动,并每隔一秒画出了蜡块运动所到达的位置如图所示,若取轨迹上的C(x,y)点作该曲线的切线(图中虚线)交y轴于A点,则A点的坐标为( )
A.(0,0.6y)
B.(0,0.5y)
C.(0,0.4y)
D.不能确定【标准解答】选B。红蜡块的运动可看作类平抛运动,则图像
的切线与竖直方向的夹角的正切值tanα= 连接OC可得直
线OC与y轴的夹角为tanθ= 所以tanθ=
即A点为竖直方向上位移的中点,所以A点的坐标为(0,0.5y),
B正确。【变式训练】在同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图所示,不计空气阻力。要使两球在空中相遇,则必须( )
A.先抛出A球
B.先抛出B球
C.同时抛出两球
D.A球的初速度大于B球的初速度【解析】选C、D。两球从同一高度抛出且能在空中相遇,表明它们被同时抛出,A、B错,C对。相同时间内,A球的水平位移较大,由x=v0t知A球的初速度较大,D对。三、圆周运动中的临界问题
1.临界状态:当物体从某种特性变化为另一种特性时发生质的飞跃的转折状态,通常叫做临界状态,出现临界状态时,既可理解为“恰好出现”,也可理解为“恰好不出现”。常见的类型有轻绳、轻杆牵引小球在竖直面内做圆周运动的条件,汽车过拱桥、摩擦力作用下物体在水平面内做圆周运动的条件。2.轻绳类:轻绳拴球在竖直面内做圆周运动,过最高点时,临界
速度为 此时F绳=0。
3.轻杆类:
(1)小球能过最高点的临界条件:v=0,F=mg,F为支持力;
(2)当0
(3)当v= 时,F=0 ;
(4)当v> 时,F随v增大而增大, F为拉力。4.汽车过拱桥:如图所示,汽车过凸形桥顶时,
桥对车的支持力F=G- 由此式可以看出汽车
对桥的压力小于汽车的重力,而且是随着汽车
速度的增大而减小;
当压力为零时,即G- =0,v= 这个速度是汽车能正常
过拱桥的临界速度。
v < 是汽车安全过桥的条件。5.摩擦力提供向心力:如图所示,物体随着水平圆盘一起转
动,汽车在水平路面上转弯,它们做圆周运动的向心力等于静
摩擦力,当静摩擦力达到最大时,物体运动速度也达到最大,
由Fm= 得vm= 这就是物体以半径r做圆周运动的临界
速度。【典例3】如图所示,杆长为L,杆的一端固定一
质量为m的小球,杆的质量忽略不计,整个系统绕
杆的另一端O在竖直平面内做圆周运动,求:
(1)小球在最高点A时速度vA为多大时,才能使杆
对小球的作用力为零?
(2)如m=0.5kg,L=0.5m,vA=0.4m/s,g=10m/s2,则在最高点A时,杆对小球的作用力是多大?是推力还是拉力?【标准解答】(1) 若杆和小球之间相互作用力为零,那么小球
做圆周运动的向心力由重力mg提供,mg= 解得:vA=
(2)杆长L=0.5 m时,临界速度v临=
=2.2 m/s,vA=0.4 m/s
答案:(1) (2)4.84 N 推力【变式训练】如图所示,AB为半径为R的金属导轨(导轨厚度不计),a、b为分别沿导轨上、下两表面做圆周运动的小球(可看作质点),要使小球不致脱离导轨,则a、b在导轨最高点的速度va、vb应满足什么条件?【解析】对a球在最高点,由牛顿第二定律得:
mag-Na= ①
要使a球不脱离轨道,则Na>0 ②
由①②得:va<
对b球在最高点,由牛顿第二定律得:
mbg+Nb= ③
要使b球不脱离轨道,则Nb>0 ④
由③④得:vb>
答案:va< vb>
