高中数学第3章空间向量与立体几何3.2.1直线的方向向量与平面的法向量课件4苏教版选修2_1(18张)
文档属性
| 名称 | 高中数学第3章空间向量与立体几何3.2.1直线的方向向量与平面的法向量课件4苏教版选修2_1(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 705.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-06 08:48:17 | ||
图片预览






文档简介
课件18张PPT。3.2.1 直线的方向向量
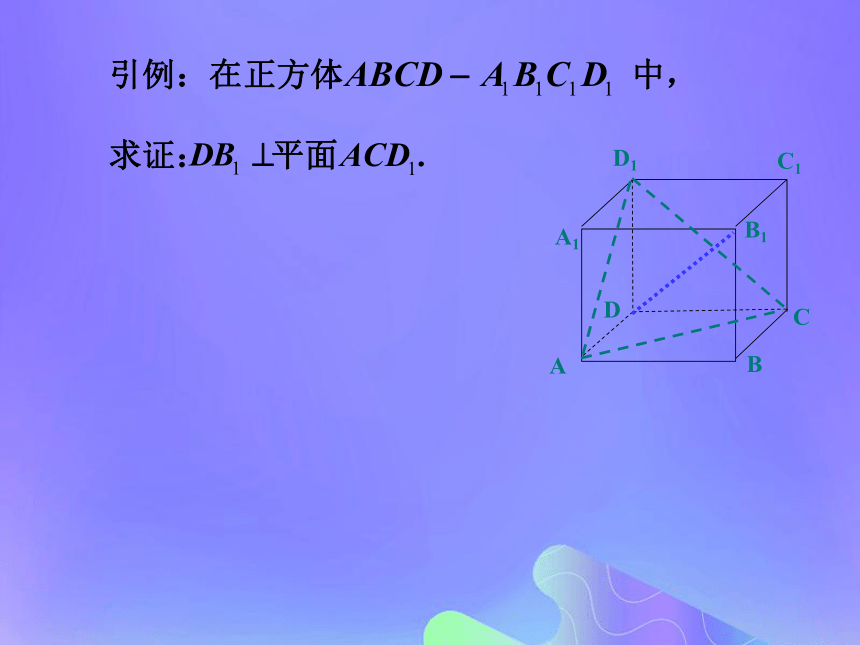
与平面的法向量引例:在正方体 中,
求证: 平面 .引例:在正方体 中,
求证: 平面 .典型例题为了用向量来研究空间的线面位置关系,首先我们要用向量来表示直线和平面的“方向”。那么如何用向量来刻画直线和平面的“方向”呢?一、直线的方向向量直线l上的非零向量 以及与 共线的非零向量叫做直线 l 的方向向量。由于垂直于同一平面的直线是互相平行的, 所以,可以用垂直于平面的直线的方向向量来刻画平面的“方向”。二、平面的法向量平面的法向量:如果表示非零向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.l概念理解下列命题中正确的是__________________
(1)平面 的法向量垂直于与平面 共面的所 有向量;
(2)一个平面的所有法向量互相平行;
(3)如果两个平面的法向量互相垂直,那么这两个平面也垂直;
(4)如果 与平面 共面,且
则 是平面 的一个法向量.(1)(2)(3)引例:在正方体 中,
求证: 平面 . 变题:例1:如何求平面 的法向量?由两个三元一次方程组成的方程组的解是不惟一的,为方便起见,取z=1较合理。其实平面的法向量不是惟一的。
平面的法向量不惟一,合理取值即可。例3:在空间直角坐标系内,设平面 经过点
,平面 的法向量为
点 是平面 内任意一点,求
满足的关系式.
解:由题意得
.因为是平面的法向量所以即:即:即:所以满足题意的关系式为:巩固性训练11.设 分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.平行垂直平行有了直线的方向向量后,可以研究他们的夹角了;两个向量是否共线或垂直,很容易判断。巩固性训练21.设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.垂直平行相交同样有了平面的法向量后,研究平面的位置关系就变得简洁些了,这也是我们下节课要研究的内容巩固性训练31、设平面 的法向量为(1,2,-2),平面 的法向量为(-2,-4,k),若 ,则k= ;若 则 k= 。
2、已知 ,且 的方向向量为(2,m,1),平面的法向量为(1,1/2,2),则m= .
3、若 的方向向量为(2,1,m),平面 的法向量为(1,1/2,2),且 ,则m= .4-5-84链接高考课堂小结(1)直线的方向向量和平面法向量的定义;
(2)证明和求解平面法向量.
与平面的法向量引例:在正方体 中,
求证: 平面 .引例:在正方体 中,
求证: 平面 .典型例题为了用向量来研究空间的线面位置关系,首先我们要用向量来表示直线和平面的“方向”。那么如何用向量来刻画直线和平面的“方向”呢?一、直线的方向向量直线l上的非零向量 以及与 共线的非零向量叫做直线 l 的方向向量。由于垂直于同一平面的直线是互相平行的, 所以,可以用垂直于平面的直线的方向向量来刻画平面的“方向”。二、平面的法向量平面的法向量:如果表示非零向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.l概念理解下列命题中正确的是__________________
(1)平面 的法向量垂直于与平面 共面的所 有向量;
(2)一个平面的所有法向量互相平行;
(3)如果两个平面的法向量互相垂直,那么这两个平面也垂直;
(4)如果 与平面 共面,且
则 是平面 的一个法向量.(1)(2)(3)引例:在正方体 中,
求证: 平面 . 变题:例1:如何求平面 的法向量?由两个三元一次方程组成的方程组的解是不惟一的,为方便起见,取z=1较合理。其实平面的法向量不是惟一的。
平面的法向量不惟一,合理取值即可。例3:在空间直角坐标系内,设平面 经过点
,平面 的法向量为
点 是平面 内任意一点,求
满足的关系式.
解:由题意得
.因为是平面的法向量所以即:即:即:所以满足题意的关系式为:巩固性训练11.设 分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.平行垂直平行有了直线的方向向量后,可以研究他们的夹角了;两个向量是否共线或垂直,很容易判断。巩固性训练21.设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.垂直平行相交同样有了平面的法向量后,研究平面的位置关系就变得简洁些了,这也是我们下节课要研究的内容巩固性训练31、设平面 的法向量为(1,2,-2),平面 的法向量为(-2,-4,k),若 ,则k= ;若 则 k= 。
2、已知 ,且 的方向向量为(2,m,1),平面的法向量为(1,1/2,2),则m= .
3、若 的方向向量为(2,1,m),平面 的法向量为(1,1/2,2),且 ,则m= .4-5-84链接高考课堂小结(1)直线的方向向量和平面法向量的定义;
(2)证明和求解平面法向量.
