2018-2019学年江苏省南通市如皋市高一(上)期末数学试卷
文档属性
| 名称 | 2018-2019学年江苏省南通市如皋市高一(上)期末数学试卷 | 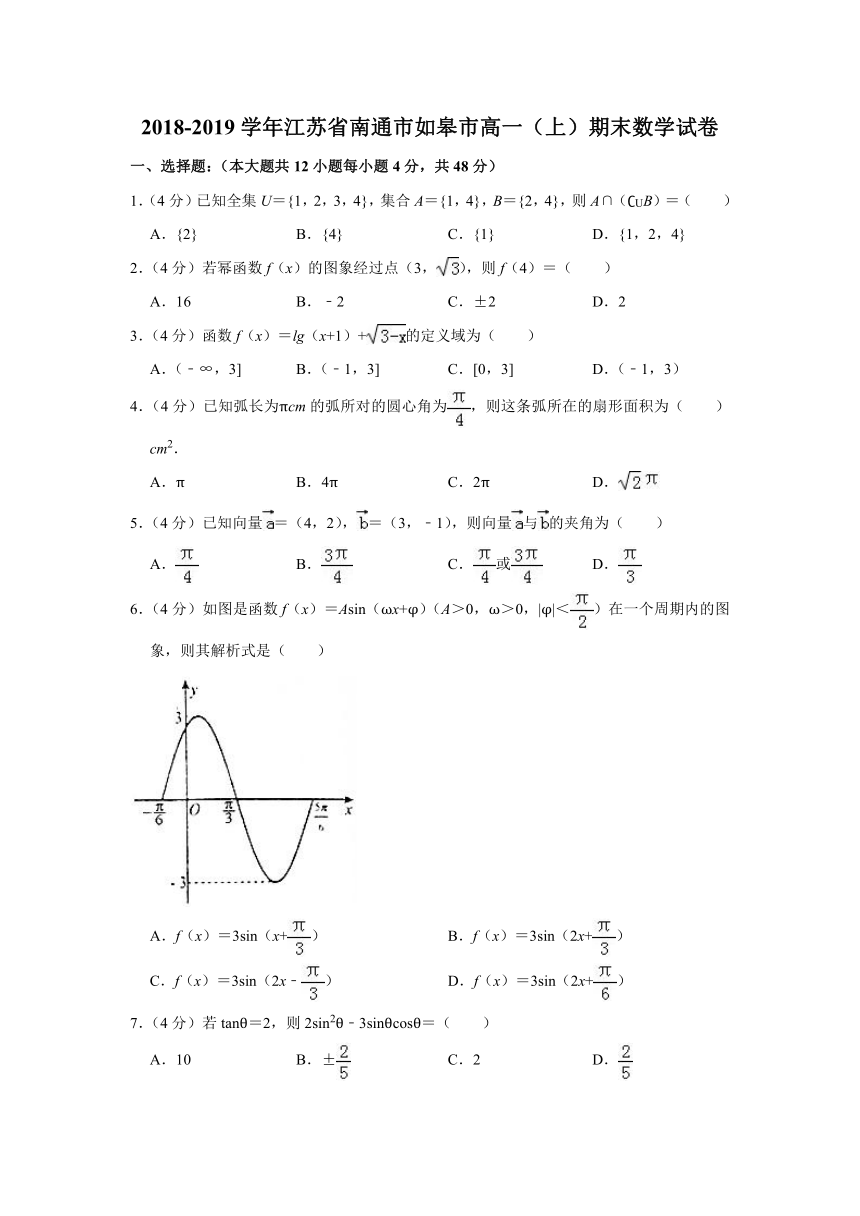 | |
| 格式 | zip | ||
| 文件大小 | 353.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-06 14:39:52 | ||
图片预览




文档简介
2018-2019学年江苏省南通市如皋市高一(上)期末数学试卷
一、选择题:(本大题共12小题每小题4分,共48分)
1.(4分)已知全集U={1,2,3,4},集合A={1,4},B={2,4},则A∩(?UB)=( )
A.{2} B.{4} C.{1} D.{1,2,4}
2.(4分)若幂函数f(x)的图象经过点(3,),则f(4)=( )
A.16 B.﹣2 C.±2 D.2
3.(4分)函数f(x)=lg(x+1)+的定义域为( )
A.(﹣∞,3] B.(﹣1,3] C.[0,3] D.(﹣1,3)
4.(4分)已知弧长为πcm的弧所对的圆心角为,则这条弧所在的扇形面积为( )cm2.
A.π B.4π C.2π D.
5.(4分)已知向量=(4,2),=(3,﹣1),则向量与的夹角为( )
A. B. C.或 D.
6.(4分)如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象,则其解析式是( )
A.f(x)=3sin(x+) B.f(x)=3sin(2x+)
C.f(x)=3sin(2x﹣) D.f(x)=3sin(2x+)
7.(4分)若tanθ=2,则2sin2θ﹣3sinθcosθ=( )
A.10 B.± C.2 D.
8.(4分)已知向量,满足||=||=||=2,则|2+|=( )
A.2 B.2 C.2 D.2
9.(4分)已知函数f(x)=,则y=f[f(x)]﹣3的零点为( )
A.0和3 B.2 C.﹣3 D.﹣1
10.(4分)在平面直角坐标系xOy中,点A,B在单位圆上,且点A在第一象限,横坐标是,将点A绕原点O顺时针旋转到B点,则点B的横坐标为( )
A. B. C. D.
11.(4分)已知函数f(x)=ex﹣e﹣x,则不等式f(2x2﹣1)+f(x)≤0的解集为( )
A.(0,1] B.[﹣] C.[﹣1,﹣] D.[﹣1,]
12.(4分)已知定义在(﹣∞,0)∪(0,+∞)上的函数f(x)=,若f(x)+f(﹣x)=0在定义域上有两个不同的解,则a的取值范围为( )
A.(﹣∞,﹣) B.()
C.(﹣∞,﹣)∪() D.(﹣)
二、填空题(本大题共4小题每小题5分,共20分)
13.(5分)计算:()﹣lg﹣lg= .
14.(5分)已知sin(α+)=,则sin(2α﹣)= .
15.(5分)三角形ABC中,已知AC=4,AB=2,=3,,=4,则= .
16.(5分)已知函数f(x)=x+,其中a∈R,若关于x的方程f(|2x﹣1|)=2a+有三个不同的实数解,则实数a的取值范围是 .
三、解答题(本大题共6小题,共82分)
17.(10分)设全集U=R,集合A={x|﹣1<x﹣m<5},B={x|<2x<4}.
(1)当m=1时,求A∩(?UB);
(2)若A∩B=?,求实数m的取值范围.
18.(12分)已知,,α,β均为锐角.
(1)求sin2α的值;
(2)求sinβ的值.
19.(14分)已知向量=(+sinx,4sinx),=(cosx+sinx,﹣cosx),设 f(x)=.
(1)将f(x)的图象向右平移个单位,然后纵坐标不变,横坐标变为原来的2倍得到g{x)的图象,求g(x)的单调增区间;
(2)若x∈[0,]时,mf(x)+m≥f(x)+2恒成立,求实数m的取值范围.
20.(14分)在三角形ABC中,AB=2,AC=1,∠ACB=,D是线段BC上一点,且=,F为线段AB上一点.
(1)设=,=,设=x+y,求x﹣y;
(2)求?的取值范围;
(3)若F为线段AB的中点,直线CF与AD相交于点M,求?.
21.(16分)如图,某城市拟在矩形区域ABCD内修建儿童乐园,已知AB=2百米,BC=4百米,点E,N分别在AD,BC上,梯形DENC为水上乐园;将梯形EABN分成三个活动区域,M在AB上,且点B,E关于MN对称,现需要修建两道栅栏ME,MN将三个活动区域隔开.设∠BNM=θ,两道栅栏的总长度L (θ)=ME+MN.
(1)求L (θ)的函数表达式,并求出函数的定义域;
(2)求L(θ)的最小值及此时θ的值.
22.(16分)若函数f(x)=x|x﹣m|+m2,m∈R.
(1)若函数f(x)为奇函数,求m的值;
(2)若函数f(x)在x∈[1,2]上是增函数,求实数m的取值范围;
(3)若函数f(x)在x∈[1,2]上的最小值为7,求实数m的值.
2018-2019学年江苏省南通市如皋市高一(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共12小题每小题4分,共48分)
1.【解答】解:∵全集U={1,2,3,4},B={2,4},
∴?UB={1,3},
∵A={1,4},
∴A∩(?UB)={1,4}∩{1,3}={1}.
故选:C.
2.【解答】解:设幂函数y=f(x)=xa,x∈R,
函数图象过点(3,),
则3a=,a=,
∴幂函数f(x)=,
∴f(4)==2.
故选:D.
3.【解答】解:由题意得:
,解得:﹣1<x≤3,
故函数的定义域是(﹣1,3],
故选:B.
4.【解答】解:∵弧长为πcm的弧所对的圆心角为,
∴半径r==4,
∴这条弧所在的扇形面积为S==2πcm2.
故选:C.
5.【解答】解:根据题意得,?=12﹣2=10
∴cos,>==
∴向量与的夹角为.
故选:A.
6.【解答】解:由图象知A=3,函数的周期T=﹣(﹣)=π,
即=π,即ω=2,
则f(x)=3sin(2x+φ),
由五点对应法得2×(﹣)+φ=0,
即φ=,
则f(x)=3sin(2x+),
故选:B.
7.【解答】解:∵sin2θ+cos2θ=1,
∴2sin2θ﹣3sinθcosθ
=
=
=
=,
故选:D.
8.【解答】解:∵;
∴=;
∴;
∴;
∴.
故选:C.
9.【解答】解:设t=f(x),
解方程f(t)﹣3=0得:
或,
解得:t=1,
即f(x)=1,
即或,
解得:x=﹣3,
故选:C.
10.【解答】解:点A,B在单位圆上,且点A在第一象限,设射线OA对应的角为θ,横坐标是cosθ=,故点A的纵坐标为sinθ=,
将点A绕原点O顺时针旋转到B点,则OB射线对应的终边对应的角为θ﹣,
则点B的横坐标为cos(θ﹣)=cosθcos+sinθsin=cosθ+sinθ=,
故选:B.
11.【解答】解:∵f(x)=ex﹣e﹣x,
∴f(﹣x)=e﹣x﹣ex=﹣(ex﹣e﹣x)=﹣f(x),
则函数f(x)是奇函数,
∵y=ex是增函数,y=e﹣x,是减函数,则f(x)=ex﹣e﹣x,是增函数,
则不等式f(2x2﹣1)+f(x)≤0得不等式f(2x2﹣1)≤﹣f(x)=f(﹣x),
则2x2﹣1≤﹣x,即2x2+x﹣1≤0,得(x+1)(2x﹣1)≤0,
得﹣1≤x≤,
即不等式的解集为[﹣1,],
故选:D.
12.【解答】解:已知定义在(﹣∞,0)∪(0,+∞)上的函数f(x)=,
若f(x)+f(﹣x)=0在定义域上有两个不同的解,等价于
直线y=x+1关于原点对称的直线y=x﹣1与函数f(x)=x2+2ax(x>0)的图象有两个交点,
联立,消y得:x2+(2a﹣1)x+1=0,
由题意有:此方程有两不等正实数根,
即,
解得:a,
故选:A.
二、填空题(本大题共4小题每小题5分,共20分)
13.【解答】解:()﹣lg﹣lg=﹣==.
故答案为:.
14.【解答】解:sin(2α﹣)=sin[2(a+)﹣]
=﹣cos2(a+)
=﹣[1﹣2sin2(a+)]
=﹣(1﹣2×)
=﹣,
故答案为:﹣
15.【解答】解:∵=3,,=4,
∴﹣=3(﹣)?3=+2;
﹣=4(﹣)?4=+3;
∴12?=(+2)?(+3)=22+32+7?)
∴12×4=2×4+3×16+7?,
∴?=﹣
故答案为:﹣
16.【解答】解:设t=g(x)=|2x﹣1|,
其图象如图所示,
设t1,t2为方程t=2a的两根
则f(|2x﹣1|)=2a+有三个不同的实数解等价于:t=g(x)的图象与直线t=t1,t=t2的交点和为3,
由图可知:t1∈(0,1),t2∈[1,+∞),
设h(x)=t2﹣(2a+)t+a,则此函数有两个零点t1∈(0,1),t2∈[1,+∞),
①当t2=1时,解得:a=,
由a=,解得t1=,满足题意,
②当t2>1时,由二次方程区间根问题可得:
,解得:a,
综合①②得:
实数a的取值范围是a,
故答案为:[,+∞).
三、解答题(本大题共6小题,共82分)
17.【解答】解:A={x|m﹣1<x<m+5},B={x|﹣1<x<2};
(1)m=1时,A={x|0<x<6},且?UB={x|x≤﹣1,或x≥2};
∴A∩(?UB)={x|2≤x<6};
(2)∵A∩B=?;
∴m﹣1≥2,或m+5≤﹣1;
∴m≥3,或m≤﹣6;
∴实数m的取值范围为{m|m≤﹣6,或m≥3}.
18.【解答】解:(1)∵,α为锐角,∴,
∴.
(2)∵α,β均为锐角,,∴α+β∈(0,π),
∴,
∴.
19.【解答】解:(1)由题意得f(x)=()2
=
=
=1+1
=2,
∴g(x)=2,
由2k,k∈Z,
得2kπ,k∈Z,
即g(x)的增区间为[],k∈Z.
(2)当x时,
可得f(x)+1∈[1,4],
∴mf(x)+m≥f(x)+2?m≥=1+,
易得1+的最大值为2,
∴使原不等式恒成立的m的范围为[2,+∞),
故实数m的取值范围为[2,+∞).
20.【解答】解:(1)∵=+=+=+(﹣)=+=+,
∴x=,y=,∴x﹣y=
(2)设=λ,(0≤λ≤1)
因为在三角形ABC中,4B=2,AC=1,∠ACB=,∴∠CAB=30°,
∴?=(﹣)?(﹣)=(λ﹣)(﹣λ)=﹣4λ2+λ?1×2×=﹣4λ2+λ=﹣4(λ﹣)2+∈[﹣4+,]
(3)∵A,M,D三点共线,∴可设=x+(1﹣x)=x+(1﹣x)?,
∵F为AB的中点,∴=+,
又C,M,F三点共线,∴存在t∈R使得=t,
∴x+(1﹣x)=+,
∴,解得,
?=(+)?=(++)?=?+2=×1×2×(﹣)+×4=﹣
21.【解答】解:(1)∵点B,E关于MN对称,
∴Rt△BMN≌RtEMN,∴BM=EM,∠BMN=∠EMN=﹣θ,
∴∠AME=π﹣2(﹣θ)=2θ,
设AM=x,则BM=EM=2﹣x,∴cos2θ==,
∴x===2﹣,
由sinθ==可得MN==,
∴ME+MN=+==.
由∠AME=2θ<可知0<θ<.
∴L (θ)=(0<θ<).
(2)∵0<θ<,∴0<sinθ<,
∴sinθ(1﹣sinθ)≤()2=,当且仅当sinθ=1﹣sinθ即sinθ=时取等号.
∴当θ=时,L(θ)取得最小值4.
22.【解答】解:(1)函数f(x)为奇函数,
∴f(0)=m2=0,解得m=0;
(2)∵f(x)=,
∵函数f(x)在x∈[1,2]上是增函数,
当m≤0时,f(x)=x2﹣mx+m2的对称轴为x=,
由≤1,即f(x)在[1,2]递增;
当0<m≤1时,f(x)=x2﹣mx+m2的对称轴为x=,
由≤1,即f(x)在[1,2]递增;
当1<m<2时,f(x)在(1,m)递减,(m,2)递增;
当m≥2时,f(x)=﹣x2+mx+m2的对称轴为x=,
若2≤m<4,可得f(x)在(1,)递增;在(,2)递减;
若m≥4,可得f(x)在(1,2)递增,
综上可得,m的范围是(﹣∞,1]∪[4,+∞);
(3)由(2)可得m≤1时,f(x)在[1,2]递增,
可得f(1)=1﹣m+m2=7,解得m=﹣2(3舍去),
当1<m<2时,f(x)在(1,m)递减,(m,2)递增,
可得f(m)=m2=7,解得m=,不符合条件,舍去;
当2≤m<4,可得f(x)在(1,)递增;在(,2)递减,
若f(1)=m﹣1+m2,f(2)=2(m﹣2)+m2,f(1)﹣f(2)=3﹣m,
当2≤m≤3,令f(2)=7,解得m=2﹣1,成立;
若3<m<4,可令f(1)=7,解得m=,不符合条件,舍去;
当m≥4,可得f(x)在(1,2)递增,令f(1)=7,
即m﹣1+m2=7,解得m=,不符合条件,舍去.
综上可得m的值为﹣2或2﹣1.
一、选择题:(本大题共12小题每小题4分,共48分)
1.(4分)已知全集U={1,2,3,4},集合A={1,4},B={2,4},则A∩(?UB)=( )
A.{2} B.{4} C.{1} D.{1,2,4}
2.(4分)若幂函数f(x)的图象经过点(3,),则f(4)=( )
A.16 B.﹣2 C.±2 D.2
3.(4分)函数f(x)=lg(x+1)+的定义域为( )
A.(﹣∞,3] B.(﹣1,3] C.[0,3] D.(﹣1,3)
4.(4分)已知弧长为πcm的弧所对的圆心角为,则这条弧所在的扇形面积为( )cm2.
A.π B.4π C.2π D.
5.(4分)已知向量=(4,2),=(3,﹣1),则向量与的夹角为( )
A. B. C.或 D.
6.(4分)如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象,则其解析式是( )
A.f(x)=3sin(x+) B.f(x)=3sin(2x+)
C.f(x)=3sin(2x﹣) D.f(x)=3sin(2x+)
7.(4分)若tanθ=2,则2sin2θ﹣3sinθcosθ=( )
A.10 B.± C.2 D.
8.(4分)已知向量,满足||=||=||=2,则|2+|=( )
A.2 B.2 C.2 D.2
9.(4分)已知函数f(x)=,则y=f[f(x)]﹣3的零点为( )
A.0和3 B.2 C.﹣3 D.﹣1
10.(4分)在平面直角坐标系xOy中,点A,B在单位圆上,且点A在第一象限,横坐标是,将点A绕原点O顺时针旋转到B点,则点B的横坐标为( )
A. B. C. D.
11.(4分)已知函数f(x)=ex﹣e﹣x,则不等式f(2x2﹣1)+f(x)≤0的解集为( )
A.(0,1] B.[﹣] C.[﹣1,﹣] D.[﹣1,]
12.(4分)已知定义在(﹣∞,0)∪(0,+∞)上的函数f(x)=,若f(x)+f(﹣x)=0在定义域上有两个不同的解,则a的取值范围为( )
A.(﹣∞,﹣) B.()
C.(﹣∞,﹣)∪() D.(﹣)
二、填空题(本大题共4小题每小题5分,共20分)
13.(5分)计算:()﹣lg﹣lg= .
14.(5分)已知sin(α+)=,则sin(2α﹣)= .
15.(5分)三角形ABC中,已知AC=4,AB=2,=3,,=4,则= .
16.(5分)已知函数f(x)=x+,其中a∈R,若关于x的方程f(|2x﹣1|)=2a+有三个不同的实数解,则实数a的取值范围是 .
三、解答题(本大题共6小题,共82分)
17.(10分)设全集U=R,集合A={x|﹣1<x﹣m<5},B={x|<2x<4}.
(1)当m=1时,求A∩(?UB);
(2)若A∩B=?,求实数m的取值范围.
18.(12分)已知,,α,β均为锐角.
(1)求sin2α的值;
(2)求sinβ的值.
19.(14分)已知向量=(+sinx,4sinx),=(cosx+sinx,﹣cosx),设 f(x)=.
(1)将f(x)的图象向右平移个单位,然后纵坐标不变,横坐标变为原来的2倍得到g{x)的图象,求g(x)的单调增区间;
(2)若x∈[0,]时,mf(x)+m≥f(x)+2恒成立,求实数m的取值范围.
20.(14分)在三角形ABC中,AB=2,AC=1,∠ACB=,D是线段BC上一点,且=,F为线段AB上一点.
(1)设=,=,设=x+y,求x﹣y;
(2)求?的取值范围;
(3)若F为线段AB的中点,直线CF与AD相交于点M,求?.
21.(16分)如图,某城市拟在矩形区域ABCD内修建儿童乐园,已知AB=2百米,BC=4百米,点E,N分别在AD,BC上,梯形DENC为水上乐园;将梯形EABN分成三个活动区域,M在AB上,且点B,E关于MN对称,现需要修建两道栅栏ME,MN将三个活动区域隔开.设∠BNM=θ,两道栅栏的总长度L (θ)=ME+MN.
(1)求L (θ)的函数表达式,并求出函数的定义域;
(2)求L(θ)的最小值及此时θ的值.
22.(16分)若函数f(x)=x|x﹣m|+m2,m∈R.
(1)若函数f(x)为奇函数,求m的值;
(2)若函数f(x)在x∈[1,2]上是增函数,求实数m的取值范围;
(3)若函数f(x)在x∈[1,2]上的最小值为7,求实数m的值.
2018-2019学年江苏省南通市如皋市高一(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共12小题每小题4分,共48分)
1.【解答】解:∵全集U={1,2,3,4},B={2,4},
∴?UB={1,3},
∵A={1,4},
∴A∩(?UB)={1,4}∩{1,3}={1}.
故选:C.
2.【解答】解:设幂函数y=f(x)=xa,x∈R,
函数图象过点(3,),
则3a=,a=,
∴幂函数f(x)=,
∴f(4)==2.
故选:D.
3.【解答】解:由题意得:
,解得:﹣1<x≤3,
故函数的定义域是(﹣1,3],
故选:B.
4.【解答】解:∵弧长为πcm的弧所对的圆心角为,
∴半径r==4,
∴这条弧所在的扇形面积为S==2πcm2.
故选:C.
5.【解答】解:根据题意得,?=12﹣2=10
∴cos,>==
∴向量与的夹角为.
故选:A.
6.【解答】解:由图象知A=3,函数的周期T=﹣(﹣)=π,
即=π,即ω=2,
则f(x)=3sin(2x+φ),
由五点对应法得2×(﹣)+φ=0,
即φ=,
则f(x)=3sin(2x+),
故选:B.
7.【解答】解:∵sin2θ+cos2θ=1,
∴2sin2θ﹣3sinθcosθ
=
=
=
=,
故选:D.
8.【解答】解:∵;
∴=;
∴;
∴;
∴.
故选:C.
9.【解答】解:设t=f(x),
解方程f(t)﹣3=0得:
或,
解得:t=1,
即f(x)=1,
即或,
解得:x=﹣3,
故选:C.
10.【解答】解:点A,B在单位圆上,且点A在第一象限,设射线OA对应的角为θ,横坐标是cosθ=,故点A的纵坐标为sinθ=,
将点A绕原点O顺时针旋转到B点,则OB射线对应的终边对应的角为θ﹣,
则点B的横坐标为cos(θ﹣)=cosθcos+sinθsin=cosθ+sinθ=,
故选:B.
11.【解答】解:∵f(x)=ex﹣e﹣x,
∴f(﹣x)=e﹣x﹣ex=﹣(ex﹣e﹣x)=﹣f(x),
则函数f(x)是奇函数,
∵y=ex是增函数,y=e﹣x,是减函数,则f(x)=ex﹣e﹣x,是增函数,
则不等式f(2x2﹣1)+f(x)≤0得不等式f(2x2﹣1)≤﹣f(x)=f(﹣x),
则2x2﹣1≤﹣x,即2x2+x﹣1≤0,得(x+1)(2x﹣1)≤0,
得﹣1≤x≤,
即不等式的解集为[﹣1,],
故选:D.
12.【解答】解:已知定义在(﹣∞,0)∪(0,+∞)上的函数f(x)=,
若f(x)+f(﹣x)=0在定义域上有两个不同的解,等价于
直线y=x+1关于原点对称的直线y=x﹣1与函数f(x)=x2+2ax(x>0)的图象有两个交点,
联立,消y得:x2+(2a﹣1)x+1=0,
由题意有:此方程有两不等正实数根,
即,
解得:a,
故选:A.
二、填空题(本大题共4小题每小题5分,共20分)
13.【解答】解:()﹣lg﹣lg=﹣==.
故答案为:.
14.【解答】解:sin(2α﹣)=sin[2(a+)﹣]
=﹣cos2(a+)
=﹣[1﹣2sin2(a+)]
=﹣(1﹣2×)
=﹣,
故答案为:﹣
15.【解答】解:∵=3,,=4,
∴﹣=3(﹣)?3=+2;
﹣=4(﹣)?4=+3;
∴12?=(+2)?(+3)=22+32+7?)
∴12×4=2×4+3×16+7?,
∴?=﹣
故答案为:﹣
16.【解答】解:设t=g(x)=|2x﹣1|,
其图象如图所示,
设t1,t2为方程t=2a的两根
则f(|2x﹣1|)=2a+有三个不同的实数解等价于:t=g(x)的图象与直线t=t1,t=t2的交点和为3,
由图可知:t1∈(0,1),t2∈[1,+∞),
设h(x)=t2﹣(2a+)t+a,则此函数有两个零点t1∈(0,1),t2∈[1,+∞),
①当t2=1时,解得:a=,
由a=,解得t1=,满足题意,
②当t2>1时,由二次方程区间根问题可得:
,解得:a,
综合①②得:
实数a的取值范围是a,
故答案为:[,+∞).
三、解答题(本大题共6小题,共82分)
17.【解答】解:A={x|m﹣1<x<m+5},B={x|﹣1<x<2};
(1)m=1时,A={x|0<x<6},且?UB={x|x≤﹣1,或x≥2};
∴A∩(?UB)={x|2≤x<6};
(2)∵A∩B=?;
∴m﹣1≥2,或m+5≤﹣1;
∴m≥3,或m≤﹣6;
∴实数m的取值范围为{m|m≤﹣6,或m≥3}.
18.【解答】解:(1)∵,α为锐角,∴,
∴.
(2)∵α,β均为锐角,,∴α+β∈(0,π),
∴,
∴.
19.【解答】解:(1)由题意得f(x)=()2
=
=
=1+1
=2,
∴g(x)=2,
由2k,k∈Z,
得2kπ,k∈Z,
即g(x)的增区间为[],k∈Z.
(2)当x时,
可得f(x)+1∈[1,4],
∴mf(x)+m≥f(x)+2?m≥=1+,
易得1+的最大值为2,
∴使原不等式恒成立的m的范围为[2,+∞),
故实数m的取值范围为[2,+∞).
20.【解答】解:(1)∵=+=+=+(﹣)=+=+,
∴x=,y=,∴x﹣y=
(2)设=λ,(0≤λ≤1)
因为在三角形ABC中,4B=2,AC=1,∠ACB=,∴∠CAB=30°,
∴?=(﹣)?(﹣)=(λ﹣)(﹣λ)=﹣4λ2+λ?1×2×=﹣4λ2+λ=﹣4(λ﹣)2+∈[﹣4+,]
(3)∵A,M,D三点共线,∴可设=x+(1﹣x)=x+(1﹣x)?,
∵F为AB的中点,∴=+,
又C,M,F三点共线,∴存在t∈R使得=t,
∴x+(1﹣x)=+,
∴,解得,
?=(+)?=(++)?=?+2=×1×2×(﹣)+×4=﹣
21.【解答】解:(1)∵点B,E关于MN对称,
∴Rt△BMN≌RtEMN,∴BM=EM,∠BMN=∠EMN=﹣θ,
∴∠AME=π﹣2(﹣θ)=2θ,
设AM=x,则BM=EM=2﹣x,∴cos2θ==,
∴x===2﹣,
由sinθ==可得MN==,
∴ME+MN=+==.
由∠AME=2θ<可知0<θ<.
∴L (θ)=(0<θ<).
(2)∵0<θ<,∴0<sinθ<,
∴sinθ(1﹣sinθ)≤()2=,当且仅当sinθ=1﹣sinθ即sinθ=时取等号.
∴当θ=时,L(θ)取得最小值4.
22.【解答】解:(1)函数f(x)为奇函数,
∴f(0)=m2=0,解得m=0;
(2)∵f(x)=,
∵函数f(x)在x∈[1,2]上是增函数,
当m≤0时,f(x)=x2﹣mx+m2的对称轴为x=,
由≤1,即f(x)在[1,2]递增;
当0<m≤1时,f(x)=x2﹣mx+m2的对称轴为x=,
由≤1,即f(x)在[1,2]递增;
当1<m<2时,f(x)在(1,m)递减,(m,2)递增;
当m≥2时,f(x)=﹣x2+mx+m2的对称轴为x=,
若2≤m<4,可得f(x)在(1,)递增;在(,2)递减;
若m≥4,可得f(x)在(1,2)递增,
综上可得,m的范围是(﹣∞,1]∪[4,+∞);
(3)由(2)可得m≤1时,f(x)在[1,2]递增,
可得f(1)=1﹣m+m2=7,解得m=﹣2(3舍去),
当1<m<2时,f(x)在(1,m)递减,(m,2)递增,
可得f(m)=m2=7,解得m=,不符合条件,舍去;
当2≤m<4,可得f(x)在(1,)递增;在(,2)递减,
若f(1)=m﹣1+m2,f(2)=2(m﹣2)+m2,f(1)﹣f(2)=3﹣m,
当2≤m≤3,令f(2)=7,解得m=2﹣1,成立;
若3<m<4,可令f(1)=7,解得m=,不符合条件,舍去;
当m≥4,可得f(x)在(1,2)递增,令f(1)=7,
即m﹣1+m2=7,解得m=,不符合条件,舍去.
综上可得m的值为﹣2或2﹣1.
同课章节目录
