18.2.1 矩形(2)课件
图片预览







文档简介
人教版数学八年级下册
18.2.1矩形(2)
想一想:矩形的定义?矩形具有哪些性质?填表回顾一下。
对边平行
对边相等
对边平行
对边相等
对角相等
四个角都直角
互相平分
互相平分且相等
矩形的定义:
有一个角是直角的平行四边形是矩形。
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
矩形的判定方法1:
有一个角是直角的平行四边形是矩形.
几何语言:
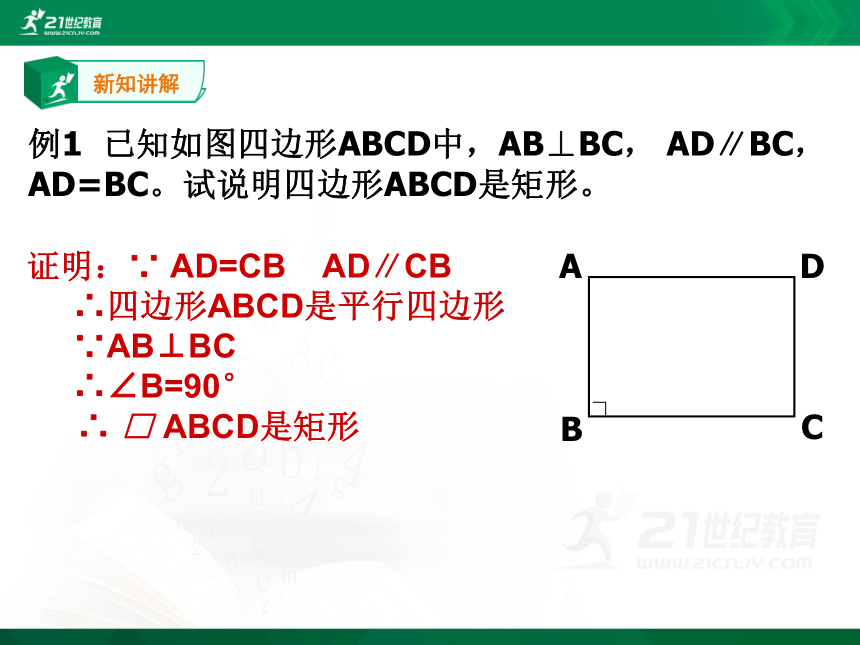
例1 已知如图四边形ABCD中,AB⊥BC, AD∥BC,AD=BC。试说明四边形ABCD是矩形。
证明:∵ AD=CB AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC
∴∠B=90°
∴ □ ABCD是矩形
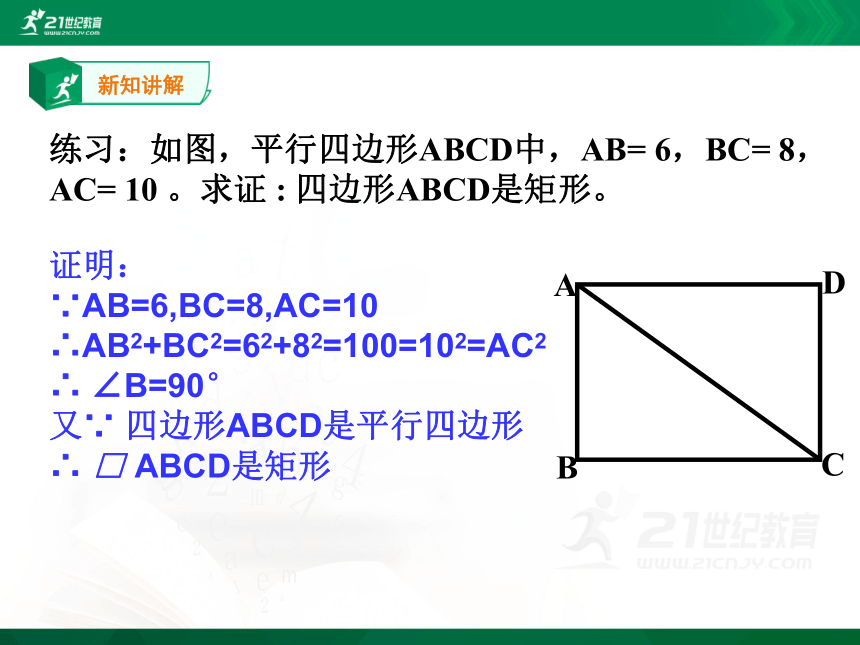
练习:如图,平行四边形ABCD中,AB= 6,BC= 8,AC= 10 。求证 : 四边形ABCD是矩形。
证明:
∵AB=6,BC=8,AC=10
∴AB2+BC2=62+82=100=102=AC2
∴ ∠B=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
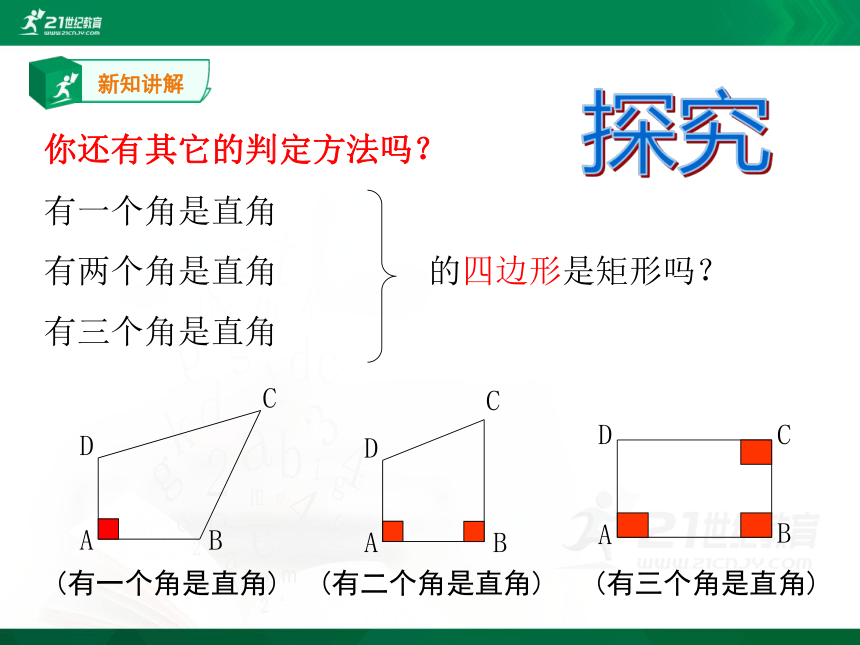
你还有其它的判定方法吗?
已知:在四边形ABCD中,∠A=∠B=∠C=90°。
求证:四边形ABCD是矩形。
证明:∵ ∠A=∠B=90°
∴ ∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵ ∠A=90°
∴四边形ABCD是矩形
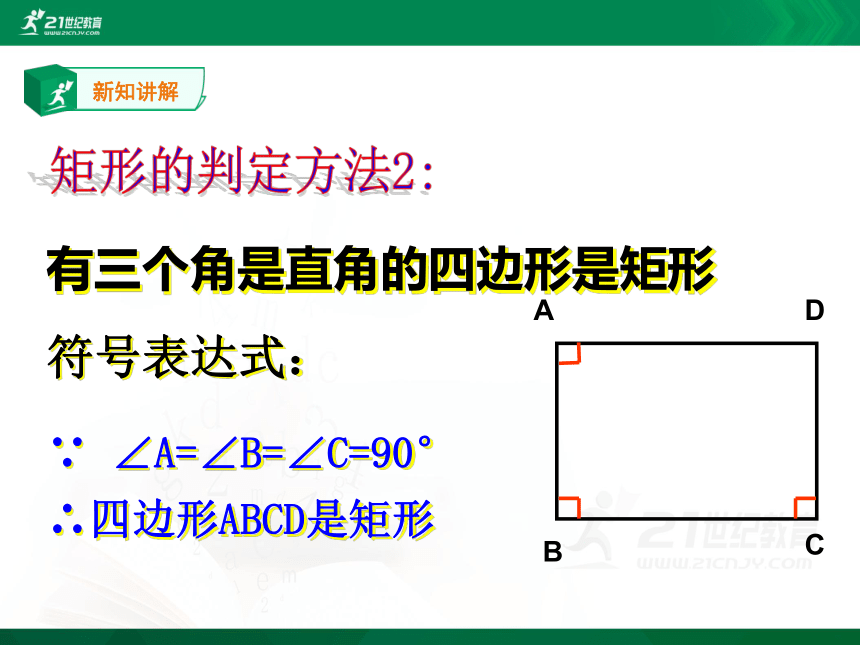
有三个角是直角的四边形是矩形
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
符号表达式:
例2 已知:如图,四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD。E、F、G、H分别是AB、BC、CD、AD的中点。求证:四边形EFGH是矩形
情境:如果工人师傅已经量得窗框的两组对边相等,接着量一量这个窗框的两条对角线长度,如果对角线长相等,窗框是矩形吗?为什么?
猜想:对角线相等的平行四边形是矩形 。
你能证明上述结论吗?
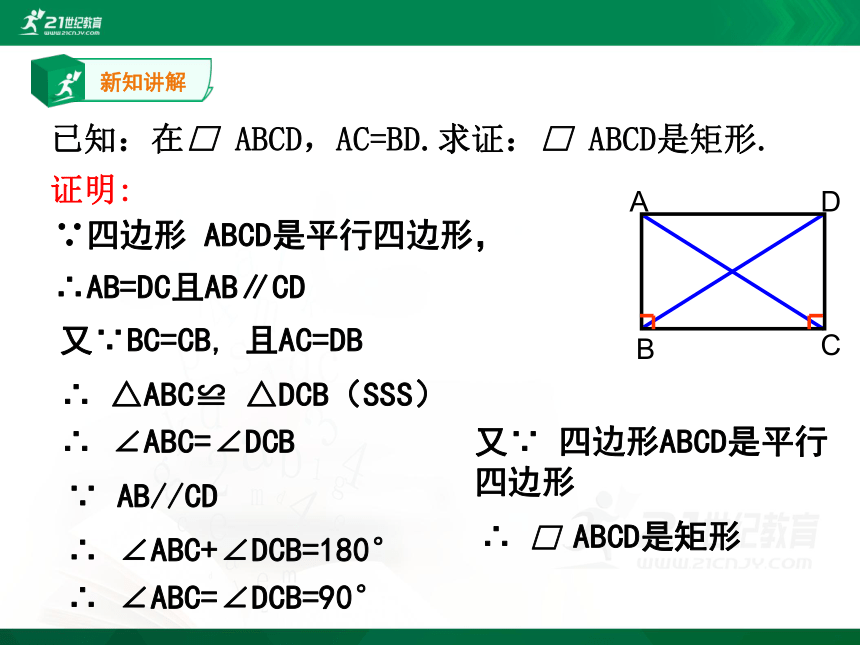
∵四边形 ABCD是平行四边形, ∴AB=DC且AB∥CD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
∴ ∠ABC=∠DCB
已知:在□ ABCD,AC=BD.求证:□ ABCD是矩形.
证明:
又∵BC=CB, 且AC=DB
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
对角线相等的平行四边形是矩形 。
矩形的判定方法3:
几何语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
(或OA=OC=OB=OD)
∴∠OAB=∠BAD-∠OAD=40°
解:
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2OD
∵OA=OD
∴AC=BD
∴四边形ABCD是矩形
∴∠BAD=90°
∵∠OAD=50°
练习:如图,四边形ABCD中AO=BO=CO=DO,
试说明四边形ABCD是矩形。
证明:
∵ AO=BO=CO=DO
∴AO=CO,BO=DO
∴四边形EFGH是平行四边形
即AC=BD
∴四边形ABCD是矩形
又∵AO+CO=BO+DO
不一定,如等腰梯形
例4 已知MN∥PQ,同旁内角的平分线AB、CB和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的数量关系是 ;
(2)试用理由说明你的猜想.
1
2
AC=BD
矩形
例5 已知:矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH。
求证:四边形EFGH是矩形。
证明:∵四边形ABCD是矩形
∴ AO=BO=CO=DO
又∵ AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形
又∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形
∵四边形ABCD是平行四边形 ∴∠DAB+∠ABC=180 °
证明:
同理:∠EFG=90°,∠FGH=90°
∴四边形EFGH是矩形
∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °
即∠AEB=90° ∴∠HEF=90°
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
(对角线互相平分且相等的四边形是矩形。)
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
测量…?
1、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形。
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
X
2、如图,M为平行四边形ABCD边AD的中点,且MB=MC。求证:四边形ABCD是矩形。
M
要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。
3、已知:平行四边形ABCD的AC、BD对角线相交于O,三角形AOB是等边三角形,AB=4cm。求这个平行四边形的面积。
5、如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形.求证:四边形ABCD是矩形.
6、在平行四边形ABCD中,对角线AC BD相交于O,EF过O,且AF⊥BC, 求证:四边形AFCE是矩形。
7、平行四边形ABCD,E是CD的中点, △ABE是等边三角形。求证:四边形ABCD是矩形。
8、BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD。求证:四边形AEBD是矩形。
9、平行四边形ABCD,AF、BH、 CH、DF分别是?BAD、?ABC、?BCD、?CDA的平分线。求证:EF=GH .
10、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当O运动到何处时, 四边形AECF为矩形?
E
F
(1)证明:∵CF平分∠ACD
∴∠1=∠2
又∵ MN∥BC
∴∠1=∠3
∴ ∠2=∠3
∴OC=OF
同理可证:OC=OE
∴OE=OF
D
(2)当点O为AC的中点时,四边形AECF是矩形。理由:
由(1)知OE=OF
又AO=CO
∴四边形AECF是平行四边形
又∵EC、FC分别平分∠ACB 、 ∠ACD
∴∠2+∠4=90°即∠ECF=90°
∴□ AECF是矩形
1、课本P60页第1、2、3、4 题
2、练习册 P 23-25 页
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.2.1矩形(2)
想一想:矩形的定义?矩形具有哪些性质?填表回顾一下。
对边平行
对边相等
对边平行
对边相等
对角相等
四个角都直角
互相平分
互相平分且相等
矩形的定义:
有一个角是直角的平行四边形是矩形。
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
矩形的判定方法1:
有一个角是直角的平行四边形是矩形.
几何语言:
例1 已知如图四边形ABCD中,AB⊥BC, AD∥BC,AD=BC。试说明四边形ABCD是矩形。
证明:∵ AD=CB AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC
∴∠B=90°
∴ □ ABCD是矩形
练习:如图,平行四边形ABCD中,AB= 6,BC= 8,AC= 10 。求证 : 四边形ABCD是矩形。
证明:
∵AB=6,BC=8,AC=10
∴AB2+BC2=62+82=100=102=AC2
∴ ∠B=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
你还有其它的判定方法吗?
已知:在四边形ABCD中,∠A=∠B=∠C=90°。
求证:四边形ABCD是矩形。
证明:∵ ∠A=∠B=90°
∴ ∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵ ∠A=90°
∴四边形ABCD是矩形
有三个角是直角的四边形是矩形
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
符号表达式:
例2 已知:如图,四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD。E、F、G、H分别是AB、BC、CD、AD的中点。求证:四边形EFGH是矩形
情境:如果工人师傅已经量得窗框的两组对边相等,接着量一量这个窗框的两条对角线长度,如果对角线长相等,窗框是矩形吗?为什么?
猜想:对角线相等的平行四边形是矩形 。
你能证明上述结论吗?
∵四边形 ABCD是平行四边形, ∴AB=DC且AB∥CD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
∴ ∠ABC=∠DCB
已知:在□ ABCD,AC=BD.求证:□ ABCD是矩形.
证明:
又∵BC=CB, 且AC=DB
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
对角线相等的平行四边形是矩形 。
矩形的判定方法3:
几何语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
(或OA=OC=OB=OD)
∴∠OAB=∠BAD-∠OAD=40°
解:
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2OD
∵OA=OD
∴AC=BD
∴四边形ABCD是矩形
∴∠BAD=90°
∵∠OAD=50°
练习:如图,四边形ABCD中AO=BO=CO=DO,
试说明四边形ABCD是矩形。
证明:
∵ AO=BO=CO=DO
∴AO=CO,BO=DO
∴四边形EFGH是平行四边形
即AC=BD
∴四边形ABCD是矩形
又∵AO+CO=BO+DO
不一定,如等腰梯形
例4 已知MN∥PQ,同旁内角的平分线AB、CB和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的数量关系是 ;
(2)试用理由说明你的猜想.
1
2
AC=BD
矩形
例5 已知:矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH。
求证:四边形EFGH是矩形。
证明:∵四边形ABCD是矩形
∴ AO=BO=CO=DO
又∵ AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形
又∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形
∵四边形ABCD是平行四边形 ∴∠DAB+∠ABC=180 °
证明:
同理:∠EFG=90°,∠FGH=90°
∴四边形EFGH是矩形
∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °
即∠AEB=90° ∴∠HEF=90°
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
(对角线互相平分且相等的四边形是矩形。)
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
测量…?
1、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形。
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
X
2、如图,M为平行四边形ABCD边AD的中点,且MB=MC。求证:四边形ABCD是矩形。
M
要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。
3、已知:平行四边形ABCD的AC、BD对角线相交于O,三角形AOB是等边三角形,AB=4cm。求这个平行四边形的面积。
5、如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形.求证:四边形ABCD是矩形.
6、在平行四边形ABCD中,对角线AC BD相交于O,EF过O,且AF⊥BC, 求证:四边形AFCE是矩形。
7、平行四边形ABCD,E是CD的中点, △ABE是等边三角形。求证:四边形ABCD是矩形。
8、BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD。求证:四边形AEBD是矩形。
9、平行四边形ABCD,AF、BH、 CH、DF分别是?BAD、?ABC、?BCD、?CDA的平分线。求证:EF=GH .
10、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当O运动到何处时, 四边形AECF为矩形?
E
F
(1)证明:∵CF平分∠ACD
∴∠1=∠2
又∵ MN∥BC
∴∠1=∠3
∴ ∠2=∠3
∴OC=OF
同理可证:OC=OE
∴OE=OF
D
(2)当点O为AC的中点时,四边形AECF是矩形。理由:
由(1)知OE=OF
又AO=CO
∴四边形AECF是平行四边形
又∵EC、FC分别平分∠ACB 、 ∠ACD
∴∠2+∠4=90°即∠ECF=90°
∴□ AECF是矩形
1、课本P60页第1、2、3、4 题
2、练习册 P 23-25 页
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
