人教版数学八年级下册 18.1平行四边形 同步测试
文档属性
| 名称 | 人教版数学八年级下册 18.1平行四边形 同步测试 |  | |
| 格式 | zip | ||
| 文件大小 | 110.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-07 14:43:15 | ||
图片预览

文档简介
18.1 平行四边形
选择题
1.如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有(B)
A.12个 B.9个 C.7个 D.5个
2.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OAD的周长为(B)
A.13 B.17
C.20 D.26
3.在四边形ABCD中,AD∥BC,如果要添加一个条件,使四边形ABCD是平行四边形,那么这个条件可能是(D)
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
4.在?ABCD中,∠A∶∠B∶∠C∶∠D的值可能是(A)
A.2∶5∶2∶5 B.3∶4∶4∶5
C.4∶4∶3∶2 D.2∶3∶5∶6
5.平行四边形的两条对角线长分别为6和10,则平行四边形的一条边的长x的取值范围为(B)
A.4<x<6 B.2<x<8
C.0<x<10 D.0<x<6
6.下面给出的是四边形ABCD中AB,BC,CD,DA的长度之比,其中能满足四边形ABCD是平行四边形的是(C)
A.1∶2∶3∶4 B.2∶2∶3∶3
C.2∶3∶2∶3 D.2∶3∶3∶2
7.(2018·黔西南)如图,在?ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则?ABCD的周长为(D)
A.26 cm
B.24 cm
C.20 cm
D.18 cm
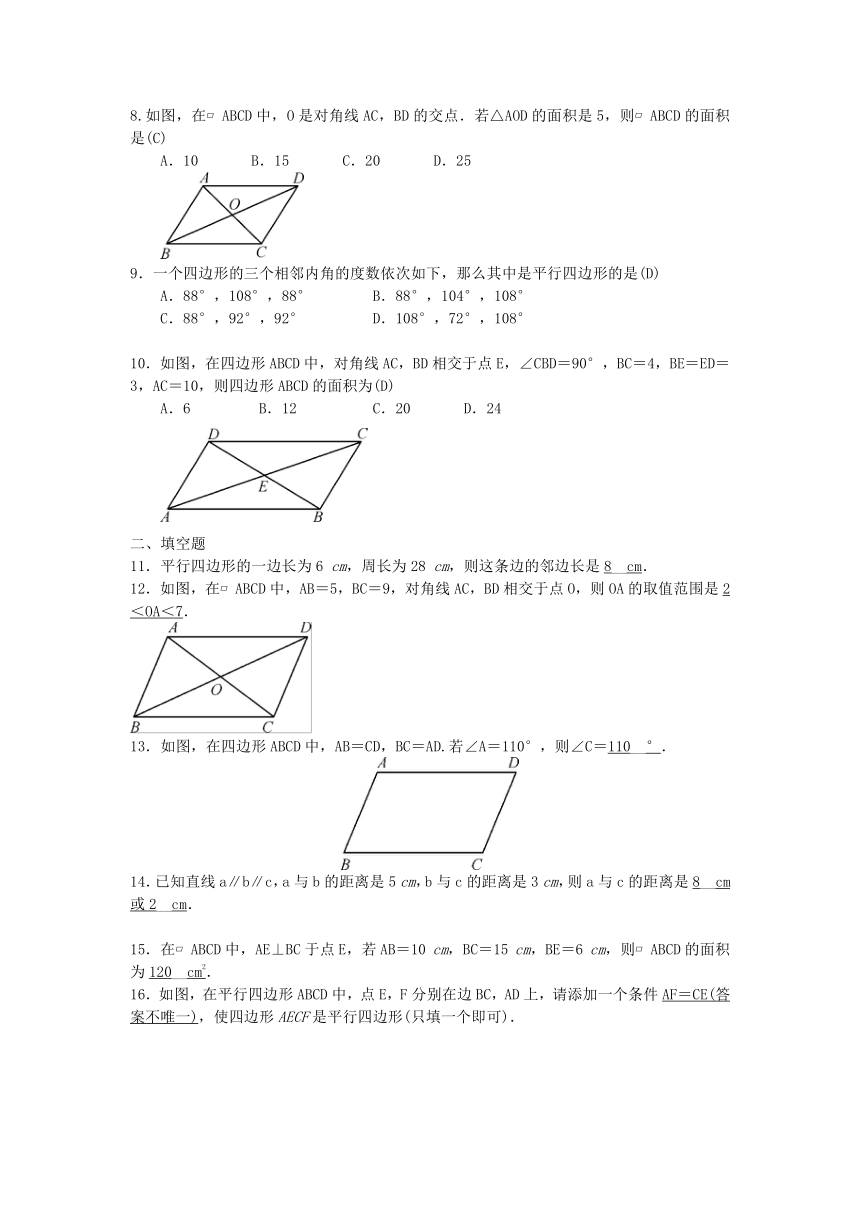
8.如图,在?ABCD中,O是对角线AC,BD的交点.若△AOD的面积是5,则?ABCD的面积是(C)
A.10 B.15 C.20 D.25
9.一个四边形的三个相邻内角的度数依次如下,那么其中是平行四边形的是(D)
A.88°,108°,88° B.88°,104°,108°
C.88°,92°,92° D.108°,72°,108°
10.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(D)
A.6 B.12 C.20 D.24
填空题
11.平行四边形的一边长为6 cm,周长为28 cm,则这条边的邻边长是8__cm.
12.如图,在?ABCD中,AB=5,BC=9,对角线AC,BD相交于点O,则OA的取值范围是2<OA<7.
13.如图,在四边形ABCD中,AB=CD,BC=AD.若∠A=110°,则∠C=110__°.
14.已知直线a∥b∥c,a与b的距离是5 cm,b与c的距离是3 cm,则a与c的距离是8__cm或2__cm.
15.在?ABCD中,AE⊥BC于点E,若AB=10 cm,BC=15 cm,BE=6 cm,则?ABCD的面积为120__cm2.
16.如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件AF=CE(答案不唯一),使四边形AECF是平行四边形(只填一个即可).
解答题
17. 如图,在?ABCD中,E,F是对角线AC上的两点,且AE=CF,求证:∠AED=∠CFB.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS).
∴∠AED=∠CFB.
18.如图,?ABCD的对角线AC,BD相交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.
(1)求AC的长;
(2)求?ABCD的面积.
解:(1)∵AO∶BO=2∶3,
∴设AO=2x,BO=3x(x>0).
∵AC⊥AB,AB=2,
∴(2x)2+(2)2=(3x)2.
解得x=2.
∴AO=4.
∵四边形ABCD是平行四边形,
∴AC=2AO=8.
(2)∵S△ABC=AB·AC
=×2×8
=8,
∴S?ABCD=2S△ABC=2×8=16.
19.如图,在?ABCD中,AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵AE=CF,
∴AB-AE=DC-CF,即BE=DF.
又∵BE∥DF,
∴四边形BFDE是平行四边形.
20.如图,?ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB.
∴∠ODF=∠OBE.
在△ODF和△OBE中,
∴△ODF≌△OBE(AAS).∴BO=DO.
(2)∵BD⊥AD,∴∠ADB=90 °.
∵∠A=45 °,∴∠DBA=∠A=45 °.
∴AD=DB.
∵EF⊥AB,∴∠G=∠A=45 °.
又∵∠ADB=90 °,∴∠DOG=∠G=45 °.
∴DO=DG.
∵AB∥CD,EF⊥AB,∴EF⊥CD.∴∠DFG=90 °.
∵∠G=45 °,∴∠GDF=∠G=45 °.
∴DF=FG=1.
∴DG==.
∵BO=DO,
∴DB=2DO=2DG=2.
∴AD=DB=2.
21.如图,在?ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.求证:
(1)四边形MNCD是平行四边形;
(2)BD=MN.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵M,N分别是AD,BC的中点,
∴MD=AD,NC=BC.∴MD=NC.
又∵MD∥NC,
∴四边形MNCD是平行四边形.
(2)连接DN.
∵N是BC的中点,BC=2CD,∴CD=NC.
∵∠C=60 °,∴△DCN是等边三角形.
∴ND=NC,∠DNC=∠NDC=60 °.
∴ND=NB=CN.
∴∠DBC=∠BDN=30 °.
∴∠BDC=∠BDN+∠NDC=90
∴BD===CD.
∵四边形MNCD是平行四边形,∴MN=CD.
∴BD=MN.
选择题
1.如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有(B)
A.12个 B.9个 C.7个 D.5个
2.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OAD的周长为(B)
A.13 B.17
C.20 D.26
3.在四边形ABCD中,AD∥BC,如果要添加一个条件,使四边形ABCD是平行四边形,那么这个条件可能是(D)
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
4.在?ABCD中,∠A∶∠B∶∠C∶∠D的值可能是(A)
A.2∶5∶2∶5 B.3∶4∶4∶5
C.4∶4∶3∶2 D.2∶3∶5∶6
5.平行四边形的两条对角线长分别为6和10,则平行四边形的一条边的长x的取值范围为(B)
A.4<x<6 B.2<x<8
C.0<x<10 D.0<x<6
6.下面给出的是四边形ABCD中AB,BC,CD,DA的长度之比,其中能满足四边形ABCD是平行四边形的是(C)
A.1∶2∶3∶4 B.2∶2∶3∶3
C.2∶3∶2∶3 D.2∶3∶3∶2
7.(2018·黔西南)如图,在?ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则?ABCD的周长为(D)
A.26 cm
B.24 cm
C.20 cm
D.18 cm
8.如图,在?ABCD中,O是对角线AC,BD的交点.若△AOD的面积是5,则?ABCD的面积是(C)
A.10 B.15 C.20 D.25
9.一个四边形的三个相邻内角的度数依次如下,那么其中是平行四边形的是(D)
A.88°,108°,88° B.88°,104°,108°
C.88°,92°,92° D.108°,72°,108°
10.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(D)
A.6 B.12 C.20 D.24
填空题
11.平行四边形的一边长为6 cm,周长为28 cm,则这条边的邻边长是8__cm.
12.如图,在?ABCD中,AB=5,BC=9,对角线AC,BD相交于点O,则OA的取值范围是2<OA<7.
13.如图,在四边形ABCD中,AB=CD,BC=AD.若∠A=110°,则∠C=110__°.
14.已知直线a∥b∥c,a与b的距离是5 cm,b与c的距离是3 cm,则a与c的距离是8__cm或2__cm.
15.在?ABCD中,AE⊥BC于点E,若AB=10 cm,BC=15 cm,BE=6 cm,则?ABCD的面积为120__cm2.
16.如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件AF=CE(答案不唯一),使四边形AECF是平行四边形(只填一个即可).
解答题
17. 如图,在?ABCD中,E,F是对角线AC上的两点,且AE=CF,求证:∠AED=∠CFB.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS).
∴∠AED=∠CFB.
18.如图,?ABCD的对角线AC,BD相交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.
(1)求AC的长;
(2)求?ABCD的面积.
解:(1)∵AO∶BO=2∶3,
∴设AO=2x,BO=3x(x>0).
∵AC⊥AB,AB=2,
∴(2x)2+(2)2=(3x)2.
解得x=2.
∴AO=4.
∵四边形ABCD是平行四边形,
∴AC=2AO=8.
(2)∵S△ABC=AB·AC
=×2×8
=8,
∴S?ABCD=2S△ABC=2×8=16.
19.如图,在?ABCD中,AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵AE=CF,
∴AB-AE=DC-CF,即BE=DF.
又∵BE∥DF,
∴四边形BFDE是平行四边形.
20.如图,?ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB.
∴∠ODF=∠OBE.
在△ODF和△OBE中,
∴△ODF≌△OBE(AAS).∴BO=DO.
(2)∵BD⊥AD,∴∠ADB=90 °.
∵∠A=45 °,∴∠DBA=∠A=45 °.
∴AD=DB.
∵EF⊥AB,∴∠G=∠A=45 °.
又∵∠ADB=90 °,∴∠DOG=∠G=45 °.
∴DO=DG.
∵AB∥CD,EF⊥AB,∴EF⊥CD.∴∠DFG=90 °.
∵∠G=45 °,∴∠GDF=∠G=45 °.
∴DF=FG=1.
∴DG==.
∵BO=DO,
∴DB=2DO=2DG=2.
∴AD=DB=2.
21.如图,在?ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.求证:
(1)四边形MNCD是平行四边形;
(2)BD=MN.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵M,N分别是AD,BC的中点,
∴MD=AD,NC=BC.∴MD=NC.
又∵MD∥NC,
∴四边形MNCD是平行四边形.
(2)连接DN.
∵N是BC的中点,BC=2CD,∴CD=NC.
∵∠C=60 °,∴△DCN是等边三角形.
∴ND=NC,∠DNC=∠NDC=60 °.
∴ND=NB=CN.
∴∠DBC=∠BDN=30 °.
∴∠BDC=∠BDN+∠NDC=90
∴BD===CD.
∵四边形MNCD是平行四边形,∴MN=CD.
∴BD=MN.
