人教版数学八年级下册17.1 勾股定理同步练习(附答案)
文档属性
| 名称 | 人教版数学八年级下册17.1 勾股定理同步练习(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-07 15:52:33 | ||
图片预览

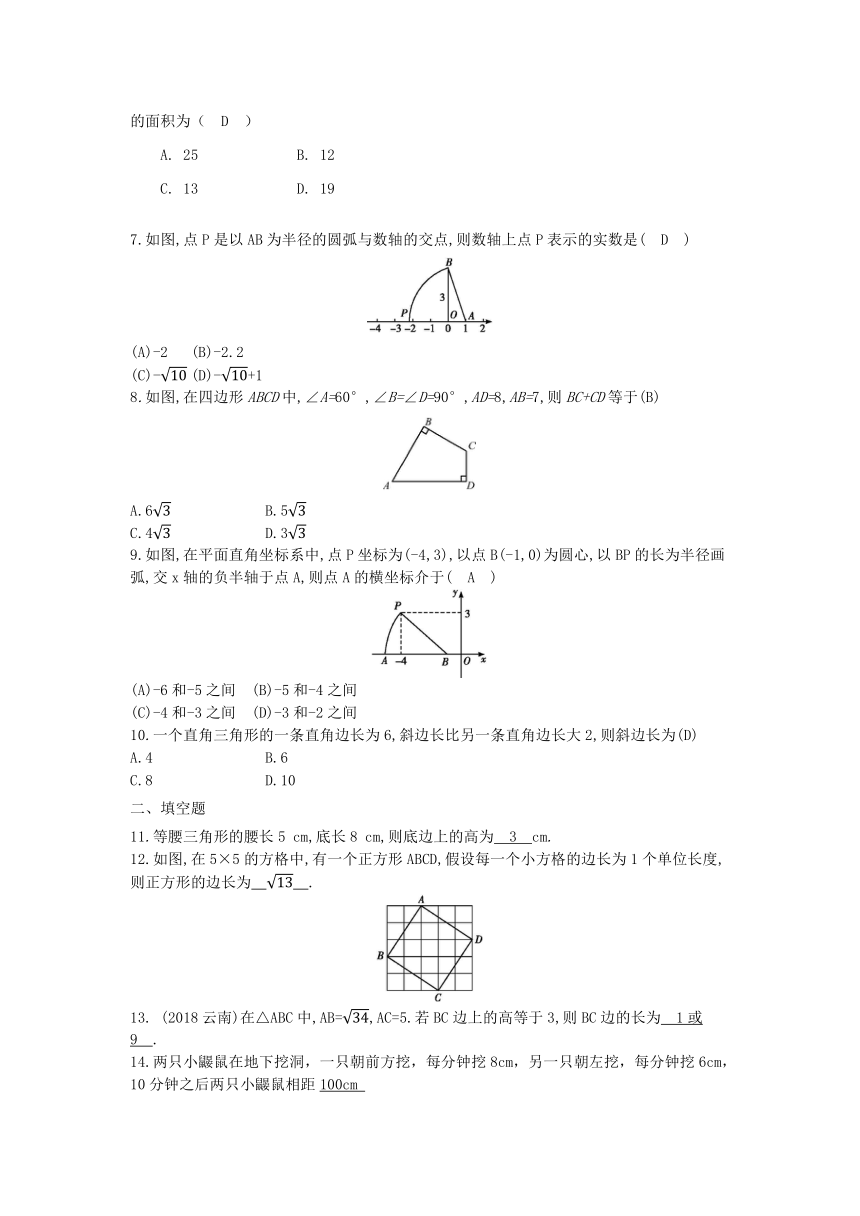
文档简介
17.1 勾股定理同步练习
一、选择题
1.在下列长度的四组线段中,不能组成直角三角形的是( D ).
A. B.
C. D.
2.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏问登陆点A与宝藏埋藏点B之间的距离是(D )km.
A. 10 B. 11 C. 12 D. 13
3.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( C )
(A) 米 (B) 米
(C)(+1)米 (D)3米
4.如果在△ABC中,AB=13,AC=15,高AD=12,那么BC的长为( B )
A. 14 B. 14或4 C. 8 D. 4和8
5.如图所示,圆柱的高AB=3,底面直径BC=3,现有一只蚂蚁想从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( C )
(A)3
(B)3
(C)
(D)3
6.E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( D )
25 B. 12
C. 13 D. 19
7.如图,点P是以AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是( D )
(A)-2 (B)-2.2
(C)- (D)-+1
8.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=8,AB=7,则BC+CD等于(B)
A.6 B.5
C.4 D.3
9.如图,在平面直角坐标系中,点P坐标为(-4,3),以点B(-1,0)为圆心,以BP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( A )
(A)-6和-5之间 (B)-5和-4之间
(C)-4和-3之间 (D)-3和-2之间
10.一个直角三角形的一条直角边长为6,斜边长比另一条直角边长大2,则斜边长为(D)
A.4 B.6
C.8 D.10
二、填空题
11.等腰三角形的腰长5 cm,底长8 cm,则底边上的高为 3 cm.
12.如图,在5×5的方格中,有一个正方形ABCD,假设每一个小方格的边长为1个单位长度,则正方形的边长为 .?
(2018云南)在△ABC中,AB=,AC=5.若BC边上的高等于3,则BC边的长为 1或9 .?
14.两只小鼹鼠在地下挖洞,一只朝前方挖,每分钟挖8cm,另一只朝左挖,每分钟挖6cm,10分钟之后两只小鼹鼠相距100cm
15.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2.则最大的正方形E的面积是 10 .?
16.(2018德州)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .?
三、计算题
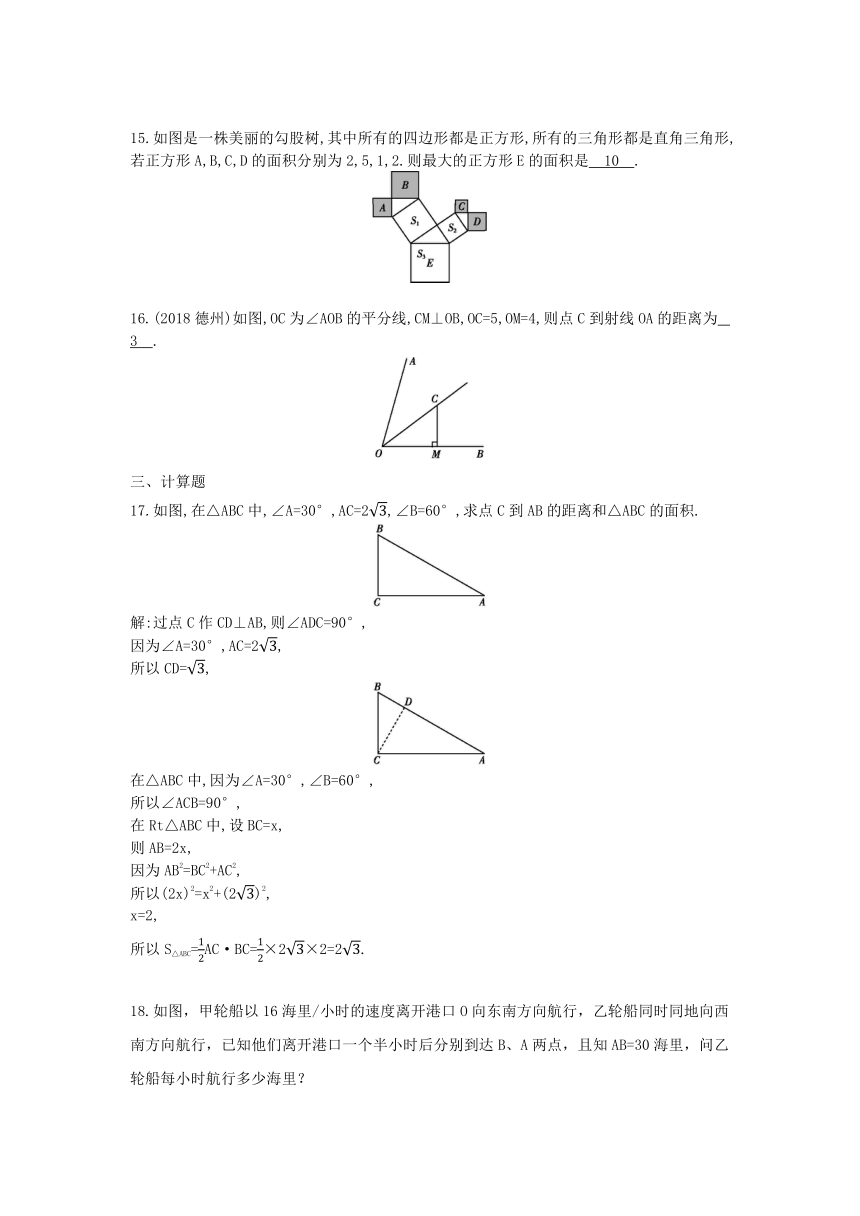
17.如图,在△ABC中,∠A=30°,AC=2,∠B=60°,求点C到AB的距离和△ABC的面积.
解:过点C作CD⊥AB,则∠ADC=90°,
因为∠A=30°,AC=2,
所以CD=,
在△ABC中,因为∠A=30°,∠B=60°,
所以∠ACB=90°,
在Rt△ABC中,设BC=x,
则AB=2x,
因为AB2=BC2+AC2,
所以(2x)2=x2+(2)2,
x=2,
所以S△ABC=AC·BC=×2×2=2.
18.如图,甲轮船以16海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,且知AB=30海里,问乙轮船每小时航行多少海里?
解:∵甲轮船向东南方向航行,乙轮船向西南方向航行,
∴AO⊥BO,
∵甲轮船以16海里/小时的速度航行了一个半小时,
∴OB=16×1.5=24海里,AB=30海里,
∴在Rt△AOB中,AO===18,
∴乙轮船每小时航行18÷1.5=12海里.
19. 如图,有一个直角三角形纸片,两直角边AC=8cm,BC=15cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
解:设CD长为,则BC=15-,由折叠知,DE=CD=,AE=AC=8
,∴BE=17-8=9, 解得 4.8
20.如图,一个长5 m的梯子AB,斜靠在一竖直的墙AO上,这时A,O的距离为4 m,如果梯子的顶端A沿墙下滑1 m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.
解:(1)根据题意得
AB=CD=5 m,AO=4 m,AC=1 m,
在Rt△AOB中,OB==3 m,
CO=AO-AC=3 m,
在Rt△COD中,OD==4 m,
BD=OD-OB=1 m.
答:梯子底端B外移距离BD的长度为1 m.
(2)CE=BE.
理由:在Rt△AOB与Rt△COD中,
所以Rt△AOB≌Rt△DOC,
所以∠OAB=∠ODC.
在△ACE与△DBE中,
所以△ACE≌△DBE,
所以CE=BE.
21.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?
解:根据题意得,在Rt△ABC中,AC=30 m,AB=50 m;
根据勾股定理可得BC===40(m),
所以小汽车的速度为v=40÷2=20(m/s)=20×3.6(km/h)=72(km/h);
因为72(km/h)>70(km/h);
所以这辆小汽车超速了.
22.如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
温馨提示:在图(3)中,作AC边上的高.
(1)解:若△ABC是钝角三角形,∠C为钝角,
则有a2+b2(2)证明:如图,过点B作BD⊥AC,
交AC的延长线于点D.
设CD为x,在Rt△BCD中,有DB2=a2-x2,
在Rt△ABD中,有DB2=c2-(b+x)2,
所以a2-x2=c2-(b+x)2,
整理得a2+b2+2bx=c2,
因为b>0,x>0,
所以2bx>0,
所以a2+b2
一、选择题
1.在下列长度的四组线段中,不能组成直角三角形的是( D ).
A. B.
C. D.
2.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏问登陆点A与宝藏埋藏点B之间的距离是(D )km.
A. 10 B. 11 C. 12 D. 13
3.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( C )
(A) 米 (B) 米
(C)(+1)米 (D)3米
4.如果在△ABC中,AB=13,AC=15,高AD=12,那么BC的长为( B )
A. 14 B. 14或4 C. 8 D. 4和8
5.如图所示,圆柱的高AB=3,底面直径BC=3,现有一只蚂蚁想从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( C )
(A)3
(B)3
(C)
(D)3
6.E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( D )
25 B. 12
C. 13 D. 19
7.如图,点P是以AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是( D )
(A)-2 (B)-2.2
(C)- (D)-+1
8.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=8,AB=7,则BC+CD等于(B)
A.6 B.5
C.4 D.3
9.如图,在平面直角坐标系中,点P坐标为(-4,3),以点B(-1,0)为圆心,以BP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( A )
(A)-6和-5之间 (B)-5和-4之间
(C)-4和-3之间 (D)-3和-2之间
10.一个直角三角形的一条直角边长为6,斜边长比另一条直角边长大2,则斜边长为(D)
A.4 B.6
C.8 D.10
二、填空题
11.等腰三角形的腰长5 cm,底长8 cm,则底边上的高为 3 cm.
12.如图,在5×5的方格中,有一个正方形ABCD,假设每一个小方格的边长为1个单位长度,则正方形的边长为 .?
(2018云南)在△ABC中,AB=,AC=5.若BC边上的高等于3,则BC边的长为 1或9 .?
14.两只小鼹鼠在地下挖洞,一只朝前方挖,每分钟挖8cm,另一只朝左挖,每分钟挖6cm,10分钟之后两只小鼹鼠相距100cm
15.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2.则最大的正方形E的面积是 10 .?
16.(2018德州)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .?
三、计算题
17.如图,在△ABC中,∠A=30°,AC=2,∠B=60°,求点C到AB的距离和△ABC的面积.
解:过点C作CD⊥AB,则∠ADC=90°,
因为∠A=30°,AC=2,
所以CD=,
在△ABC中,因为∠A=30°,∠B=60°,
所以∠ACB=90°,
在Rt△ABC中,设BC=x,
则AB=2x,
因为AB2=BC2+AC2,
所以(2x)2=x2+(2)2,
x=2,
所以S△ABC=AC·BC=×2×2=2.
18.如图,甲轮船以16海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,且知AB=30海里,问乙轮船每小时航行多少海里?
解:∵甲轮船向东南方向航行,乙轮船向西南方向航行,
∴AO⊥BO,
∵甲轮船以16海里/小时的速度航行了一个半小时,
∴OB=16×1.5=24海里,AB=30海里,
∴在Rt△AOB中,AO===18,
∴乙轮船每小时航行18÷1.5=12海里.
19. 如图,有一个直角三角形纸片,两直角边AC=8cm,BC=15cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
解:设CD长为,则BC=15-,由折叠知,DE=CD=,AE=AC=8
,∴BE=17-8=9, 解得 4.8
20.如图,一个长5 m的梯子AB,斜靠在一竖直的墙AO上,这时A,O的距离为4 m,如果梯子的顶端A沿墙下滑1 m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.
解:(1)根据题意得
AB=CD=5 m,AO=4 m,AC=1 m,
在Rt△AOB中,OB==3 m,
CO=AO-AC=3 m,
在Rt△COD中,OD==4 m,
BD=OD-OB=1 m.
答:梯子底端B外移距离BD的长度为1 m.
(2)CE=BE.
理由:在Rt△AOB与Rt△COD中,
所以Rt△AOB≌Rt△DOC,
所以∠OAB=∠ODC.
在△ACE与△DBE中,
所以△ACE≌△DBE,
所以CE=BE.
21.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?
解:根据题意得,在Rt△ABC中,AC=30 m,AB=50 m;
根据勾股定理可得BC===40(m),
所以小汽车的速度为v=40÷2=20(m/s)=20×3.6(km/h)=72(km/h);
因为72(km/h)>70(km/h);
所以这辆小汽车超速了.
22.如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
温馨提示:在图(3)中,作AC边上的高.
(1)解:若△ABC是钝角三角形,∠C为钝角,
则有a2+b2
交AC的延长线于点D.
设CD为x,在Rt△BCD中,有DB2=a2-x2,
在Rt△ABD中,有DB2=c2-(b+x)2,
所以a2-x2=c2-(b+x)2,
整理得a2+b2+2bx=c2,
因为b>0,x>0,
所以2bx>0,
所以a2+b2
