山东省平原县育才中学2018-2019年八年级数学17.2《勾股定理的逆定理》同步测试(含答案)
文档属性
| 名称 | 山东省平原县育才中学2018-2019年八年级数学17.2《勾股定理的逆定理》同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 153.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-07 22:52:15 | ||
图片预览


文档简介
2018-2019年八年级数学17.2《勾股定理的逆定理》同步测试
一、选择题:
1、长度为9、12、15、36、39的五根木棍,从中取三根依次搭成三角形,最多可搭成直角三角形的个数是( )
A.1 B.2 C.3 D.4
2、直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( ).
A.30 B.28 C.56 D.不能确定
3、下列条件中,不能判断一个三角形是直角三角形的是( )
A.三个角的比为1:2:3?? B.三条边满足关系a2=b2﹣c2
C.三条边的比为1:2:3?? D.三个角满足关系∠B+∠C=∠A
4、在△ABC中,∠A,∠B,∠C的对边分别为a,b,c且(a+b)(a-b)=c2,则( )
A. ∠A为直角?????????????B. ∠C为直角?????????????
?C. ∠B为直角?????????????D. △ABC不是直角三角形
5、如图所示,在由单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成直角三角形三边的线段是( )
A.CD,EF,GH B.AB,EF,GH
C.AB,CD,GH D.AB,CD,EF
6、直角三角形的三边为a﹣b,a,a+b且a、b都为正整数,则三角形其中一边长可能为( )
A.61?? B.71?? C.81?? D.91
7、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为(? )
A.?5????????B.?25???????C.?7????????D.?15
8、以下定理,其中有逆定理的是( )
A. 对顶角相等?????????????
?B. 互为邻补角的角平分线互相垂直?????????????
?C. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补?????
D. 直角三角形的两条直角边的平方和等于斜边的平方
9、已知三角形的三边长为n、n+1、m(其中m2=2n+1),则此三角形( ).
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
10、我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
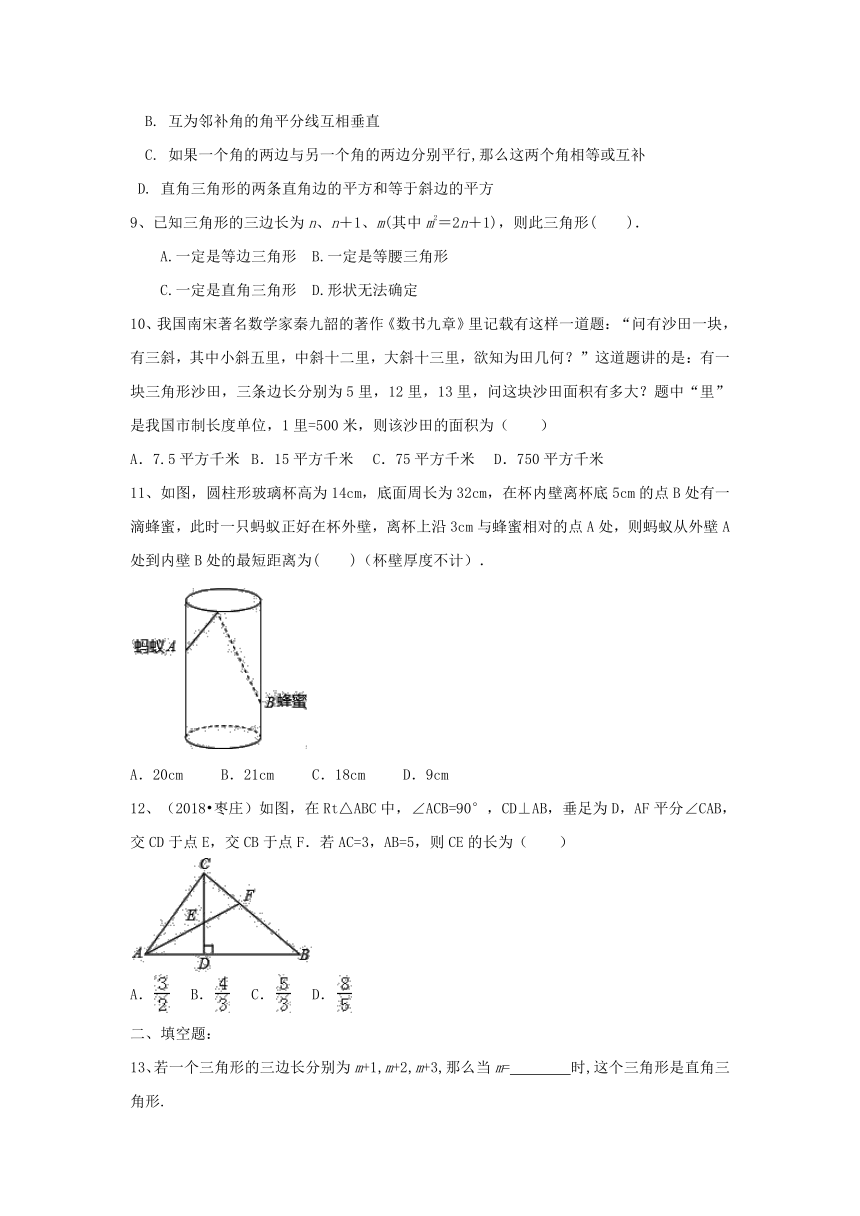
11、如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )(杯壁厚度不计).
A.20cm?? B.21cm?? C.18cm?? D.9cm
12、(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. B. C. D.
二、填空题:
13、若一个三角形的三边长分别为m+1,m+2,m+3,那么当m= 时,这个三角形是直角三角形.?
14、一根24米绳子,折成三边为三个连续偶数的三角形,则最短的边长为 ,此三角形的形状为 。
15、分别以下列四组数为一个三角形的边长:(1)6、8、10,(2)5、12、13,(3)8、15、17,(4)4、5、6,其中能构成直角三角形的有____________.(填序号)
16、已知a,b,c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为___________.
17、直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长 .
18、如图,已知Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE=________?cm.
19、已知一个Rt△的两边长分别为3和4,则第三边长的平方是 .
20、若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a+2为边的三角形的面积为______.
21、一个三角形的三边长为15,20,25,则此三角形最大边上的高为 .
22、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为 .
三、解答题:
23、如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
24、如图,在△ABC中,D是BC边上一点,已知AB=15,AD=12,AC=13,CD=5,求BD的长.
25、已知:如图,∠DAC=∠EAC,AD=AE,D为BC上一点,且BD=DC,AC2=AE2+CE2。求证:AB2=AE2+CE2。
26、如图,一根长6√3米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ ABO)为 60°.当木棒 A 端沿墙下滑至点A′时,B 端沿地面向右滑行至点 B′.
求 OB 的长;
当 AA′=1 米时,求BB′的长.
27、(2018?台湾)嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 编号 图例 行径位置
第一条路径 R1 _ A→C→D→B
第二条路径 R2 … A→E→D→F→B
第三条路径 R3 ▂ A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
一、选择题:
1、B
2、D
3、C
4、A
5、B
6、C
7、C
8、D
9、C
10、A
11、A
12、A
二、填空题:
13、2
14、6m 直角三角形
15、(1)(2)(3)
16、等腰直角三角形
17、10cm
18、1.875
19、7或25
20、8
21、8
22、3
三、解答题:
23、解:△ABD为直角三角形.理由如下: ∵在△ABC中,∠C=90°,
∴AB2=CB2+AC2=42+32=52 ,
∴在△ABD中,AB2+AD2=52+122=132 ,
∴AB2+AD2=BD2 ,
∴△ABD为直角三角形.
24、解:在△ACD中,AD2+CD2=122+52=169,AC2=132=169,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
且∠ADC=90°.
在Rt△ABD中,BD2=AB2-AD2=152-122=81,
∴BD=9
25、AC2=AE2+CE2得∠E=90°;由△ADC≌△AEC,得AD=AE,CD=CE,∠ADC=∠AEC=90°,根据线段垂直平分线的判定可知AB=AC,则AB2=AE2+CE2。
所以为直角三角形
26、(1)OB的长为3√3米;
(2)BB′=(2√11﹣3√3)米.
27、解:第一条路径的长度为++=2+,
第二条路径的长度为++1+=+++1,
第三条路径的长度为+=2+,
∵2+<2+<+++1,
∴最长路径为A→E→D→F→B;最短路径为A→G→B.
一、选择题:
1、长度为9、12、15、36、39的五根木棍,从中取三根依次搭成三角形,最多可搭成直角三角形的个数是( )
A.1 B.2 C.3 D.4
2、直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( ).
A.30 B.28 C.56 D.不能确定
3、下列条件中,不能判断一个三角形是直角三角形的是( )
A.三个角的比为1:2:3?? B.三条边满足关系a2=b2﹣c2
C.三条边的比为1:2:3?? D.三个角满足关系∠B+∠C=∠A
4、在△ABC中,∠A,∠B,∠C的对边分别为a,b,c且(a+b)(a-b)=c2,则( )
A. ∠A为直角?????????????B. ∠C为直角?????????????
?C. ∠B为直角?????????????D. △ABC不是直角三角形
5、如图所示,在由单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成直角三角形三边的线段是( )
A.CD,EF,GH B.AB,EF,GH
C.AB,CD,GH D.AB,CD,EF
6、直角三角形的三边为a﹣b,a,a+b且a、b都为正整数,则三角形其中一边长可能为( )
A.61?? B.71?? C.81?? D.91
7、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为(? )
A.?5????????B.?25???????C.?7????????D.?15
8、以下定理,其中有逆定理的是( )
A. 对顶角相等?????????????
?B. 互为邻补角的角平分线互相垂直?????????????
?C. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补?????
D. 直角三角形的两条直角边的平方和等于斜边的平方
9、已知三角形的三边长为n、n+1、m(其中m2=2n+1),则此三角形( ).
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
10、我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
11、如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )(杯壁厚度不计).
A.20cm?? B.21cm?? C.18cm?? D.9cm
12、(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. B. C. D.
二、填空题:
13、若一个三角形的三边长分别为m+1,m+2,m+3,那么当m= 时,这个三角形是直角三角形.?
14、一根24米绳子,折成三边为三个连续偶数的三角形,则最短的边长为 ,此三角形的形状为 。
15、分别以下列四组数为一个三角形的边长:(1)6、8、10,(2)5、12、13,(3)8、15、17,(4)4、5、6,其中能构成直角三角形的有____________.(填序号)
16、已知a,b,c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为___________.
17、直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长 .
18、如图,已知Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE=________?cm.
19、已知一个Rt△的两边长分别为3和4,则第三边长的平方是 .
20、若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a+2为边的三角形的面积为______.
21、一个三角形的三边长为15,20,25,则此三角形最大边上的高为 .
22、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为 .
三、解答题:
23、如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
24、如图,在△ABC中,D是BC边上一点,已知AB=15,AD=12,AC=13,CD=5,求BD的长.
25、已知:如图,∠DAC=∠EAC,AD=AE,D为BC上一点,且BD=DC,AC2=AE2+CE2。求证:AB2=AE2+CE2。
26、如图,一根长6√3米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ ABO)为 60°.当木棒 A 端沿墙下滑至点A′时,B 端沿地面向右滑行至点 B′.
求 OB 的长;
当 AA′=1 米时,求BB′的长.
27、(2018?台湾)嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 编号 图例 行径位置
第一条路径 R1 _ A→C→D→B
第二条路径 R2 … A→E→D→F→B
第三条路径 R3 ▂ A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
一、选择题:
1、B
2、D
3、C
4、A
5、B
6、C
7、C
8、D
9、C
10、A
11、A
12、A
二、填空题:
13、2
14、6m 直角三角形
15、(1)(2)(3)
16、等腰直角三角形
17、10cm
18、1.875
19、7或25
20、8
21、8
22、3
三、解答题:
23、解:△ABD为直角三角形.理由如下: ∵在△ABC中,∠C=90°,
∴AB2=CB2+AC2=42+32=52 ,
∴在△ABD中,AB2+AD2=52+122=132 ,
∴AB2+AD2=BD2 ,
∴△ABD为直角三角形.
24、解:在△ACD中,AD2+CD2=122+52=169,AC2=132=169,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
且∠ADC=90°.
在Rt△ABD中,BD2=AB2-AD2=152-122=81,
∴BD=9
25、AC2=AE2+CE2得∠E=90°;由△ADC≌△AEC,得AD=AE,CD=CE,∠ADC=∠AEC=90°,根据线段垂直平分线的判定可知AB=AC,则AB2=AE2+CE2。
所以为直角三角形
26、(1)OB的长为3√3米;
(2)BB′=(2√11﹣3√3)米.
27、解:第一条路径的长度为++=2+,
第二条路径的长度为++1+=+++1,
第三条路径的长度为+=2+,
∵2+<2+<+++1,
∴最长路径为A→E→D→F→B;最短路径为A→G→B.
