山东省东明县南华中学2019年八年级数学17.2《勾股定理的逆定理》同步测试(含答案)
文档属性
| 名称 | 山东省东明县南华中学2019年八年级数学17.2《勾股定理的逆定理》同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 75.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-07 00:00:00 | ||
图片预览


文档简介
八年级数学17.2《勾股定理的逆定理》同步测试
一、选择题:
1、下列四组线段中,可以构成直角三角形的是(???)
A.?1,2,3????????????????????????????B.?2,3,4????????????????????????????C.?3,4,5????????????????????????????D.?4,5,6
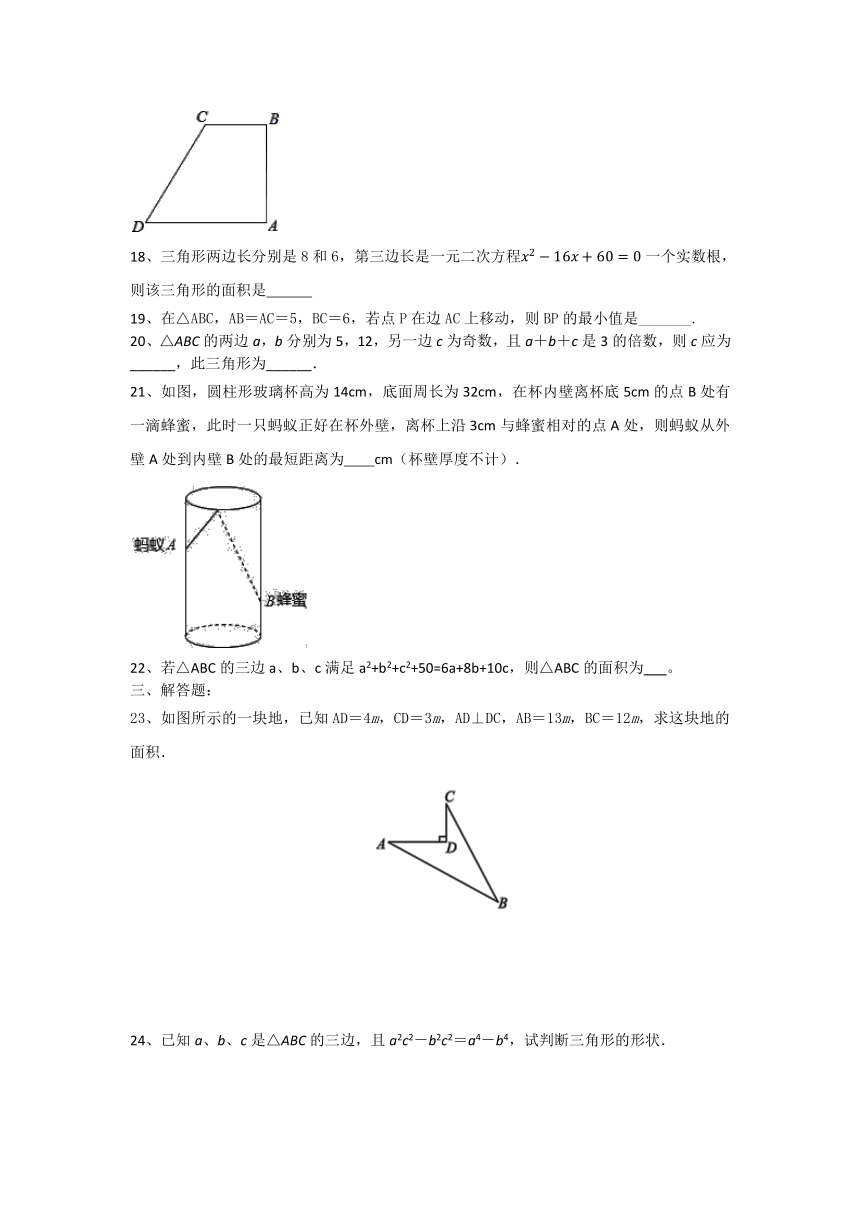
2、直角三角形的三边为a﹣b,a,a+b且a、b都为正整数,则三角形其中一边长可能为( )
A.61?? B.71?? C.81?? D.91
3、满足下列条件的三角形中,不是直角三角形的是 ( )
A. 三内角之比为1∶2∶3?????????????B. 三边长的平方之比为1∶2∶3?????????????
?C. 三边长之比为3∶4∶5?????????????D. 三内角之比为3∶4∶5????
4、小明和小刚二人同时从学校步行去公园,速度都是50 m/min,小明从学校直接去公园走直线用了10 min,而小刚走直线从学校出发先回家用时6 min,再去公园,用时8 min,则小刚从学校到公园走了个( )
A.锐角弯 B.钝角弯 C.直角弯 D.不能确定
5、在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列判断错误的是( )
A. 如果∠C-∠B=∠A,则△ABC是直角三角形
B. 如果a2+c2=b2,则△ABC不是直角三角形
C. 如果(c-a)(c+a)=b2,则△ABC是直角三角形
D. 如果∠A∶∠B∶∠C=5∶2∶3,则△ABC是直角三角形
6、下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c , 若a2+b2=c2 , 则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy .
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
7、将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )
A.直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等腰三角形.
8、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为(? )
A.?5??????????????????????????????????????????B.?25??????????????????????????????????????????C.?7??????????????????????????????????????????D.?15
9、一个三角形的三边长为15,20,25,则此三角形最大边上的高为(???)
A. 10 B. 12 C. 24 D. 48
10、(2018?东营)如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A. B. C. D.
11、直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( )
A.4 cm B.8 cm C.10 cm D.12 cm
12、(2018?泸州)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
二、填空题:
13、如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是______三角形,我们把这个定理叫做勾股定理的______.
14、已知|m﹣|++(p﹣)2=0则以m、n、p为三边长的三角形是 三角形.
15、等腰三角形的腰长为10,底长为12,则其底边上的高为
16、三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是 .
17、如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为________.
18、三角形两边长分别是8和6,第三边长是一元二次方程一个实数根,则该三角形的面积是
19、在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
20、△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为______,此三角形为______.
21、如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
22、若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,则△ABC的面积为 。
三、解答题:
23、如图所示的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,求这块地的面积.
24、已知a、b、c是△ABC的三边,且a2c2-b2c2=a4-b4,试判断三角形的形状.
25、如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.
(1)此时,A,B两组行进的方向成直角吗?请说明理由;
(2)若A,B两组仍以原速前进,相向而行,经过几小时后相遇?
26、在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?
27、如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
(
A
B
C
D
L
)
一、选择题:
1、C
2、C
3、D
4、C
5、B
6、C
7、A
8、C
9、B
10、C
11、C
12、D
二、填空题:
13、直角 逆定理
14、等腰直角
15、8
16、直角三角形
17、2或4或2√3
18、24或
19、24/5
20、13,直角三角形
21、20
22、6
三、解答题:
23、连接AC,由勾股定理得AC==5,
又∵BC=12,AB=13,
∴∠ACB=90°,
∴这块地的面积=S△ABC-S△ACD=×5×12-×3×4=30-6=24(m2)
24、原式可变形为(a2-b2)(a2+b2-c2)=0.
a2-b2=0 a=b 等腰三角形
a2+b2-c2=0. a2+b2=c2. 直角三角形
三角形为等腰三角形或直角三角形
25、(1)出发2小时,A组行了12×2=24千米,B组行了9×2=18千米,
这时A,B两组相距30千米,
且有242+182=302,
所以A,B两组行进的方向成直角.
(2)30÷(12+9)=10/7小时相遇
26、如图,甲船航行的距离为BM=8×2=16(海里),乙船航行的距离为BP=15×2=30(海里).
?
?∵162+302=1?156=342,∴BM2+BP2=MP2,
?∴△MBP为直角三角形,且∠MBP=90°,
?∴乙船是沿着南偏东30°的方向航行的.
27、作A点关于CD的对称点A′,连结B A′,与CD交于点E,则E点即为所求.总费用150万元.
一、选择题:
1、下列四组线段中,可以构成直角三角形的是(???)
A.?1,2,3????????????????????????????B.?2,3,4????????????????????????????C.?3,4,5????????????????????????????D.?4,5,6
2、直角三角形的三边为a﹣b,a,a+b且a、b都为正整数,则三角形其中一边长可能为( )
A.61?? B.71?? C.81?? D.91
3、满足下列条件的三角形中,不是直角三角形的是 ( )
A. 三内角之比为1∶2∶3?????????????B. 三边长的平方之比为1∶2∶3?????????????
?C. 三边长之比为3∶4∶5?????????????D. 三内角之比为3∶4∶5????
4、小明和小刚二人同时从学校步行去公园,速度都是50 m/min,小明从学校直接去公园走直线用了10 min,而小刚走直线从学校出发先回家用时6 min,再去公园,用时8 min,则小刚从学校到公园走了个( )
A.锐角弯 B.钝角弯 C.直角弯 D.不能确定
5、在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列判断错误的是( )
A. 如果∠C-∠B=∠A,则△ABC是直角三角形
B. 如果a2+c2=b2,则△ABC不是直角三角形
C. 如果(c-a)(c+a)=b2,则△ABC是直角三角形
D. 如果∠A∶∠B∶∠C=5∶2∶3,则△ABC是直角三角形
6、下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c , 若a2+b2=c2 , 则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy .
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
7、将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )
A.直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等腰三角形.
8、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为(? )
A.?5??????????????????????????????????????????B.?25??????????????????????????????????????????C.?7??????????????????????????????????????????D.?15
9、一个三角形的三边长为15,20,25,则此三角形最大边上的高为(???)
A. 10 B. 12 C. 24 D. 48
10、(2018?东营)如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A. B. C. D.
11、直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( )
A.4 cm B.8 cm C.10 cm D.12 cm
12、(2018?泸州)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
二、填空题:
13、如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是______三角形,我们把这个定理叫做勾股定理的______.
14、已知|m﹣|++(p﹣)2=0则以m、n、p为三边长的三角形是 三角形.
15、等腰三角形的腰长为10,底长为12,则其底边上的高为
16、三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是 .
17、如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为________.
18、三角形两边长分别是8和6,第三边长是一元二次方程一个实数根,则该三角形的面积是
19、在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
20、△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为______,此三角形为______.
21、如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
22、若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,则△ABC的面积为 。
三、解答题:
23、如图所示的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,求这块地的面积.
24、已知a、b、c是△ABC的三边,且a2c2-b2c2=a4-b4,试判断三角形的形状.
25、如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.
(1)此时,A,B两组行进的方向成直角吗?请说明理由;
(2)若A,B两组仍以原速前进,相向而行,经过几小时后相遇?
26、在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?
27、如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
(
A
B
C
D
L
)
一、选择题:
1、C
2、C
3、D
4、C
5、B
6、C
7、A
8、C
9、B
10、C
11、C
12、D
二、填空题:
13、直角 逆定理
14、等腰直角
15、8
16、直角三角形
17、2或4或2√3
18、24或
19、24/5
20、13,直角三角形
21、20
22、6
三、解答题:
23、连接AC,由勾股定理得AC==5,
又∵BC=12,AB=13,
∴∠ACB=90°,
∴这块地的面积=S△ABC-S△ACD=×5×12-×3×4=30-6=24(m2)
24、原式可变形为(a2-b2)(a2+b2-c2)=0.
a2-b2=0 a=b 等腰三角形
a2+b2-c2=0. a2+b2=c2. 直角三角形
三角形为等腰三角形或直角三角形
25、(1)出发2小时,A组行了12×2=24千米,B组行了9×2=18千米,
这时A,B两组相距30千米,
且有242+182=302,
所以A,B两组行进的方向成直角.
(2)30÷(12+9)=10/7小时相遇
26、如图,甲船航行的距离为BM=8×2=16(海里),乙船航行的距离为BP=15×2=30(海里).
?
?∵162+302=1?156=342,∴BM2+BP2=MP2,
?∴△MBP为直角三角形,且∠MBP=90°,
?∴乙船是沿着南偏东30°的方向航行的.
27、作A点关于CD的对称点A′,连结B A′,与CD交于点E,则E点即为所求.总费用150万元.
