高中数学第3章空间向量与立体几何3.2.3空间的角的计算课件 苏教版选修2_1(16张PPT)
文档属性
| 名称 | 高中数学第3章空间向量与立体几何3.2.3空间的角的计算课件 苏教版选修2_1(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 868.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-08 00:00:00 | ||
图片预览





文档简介
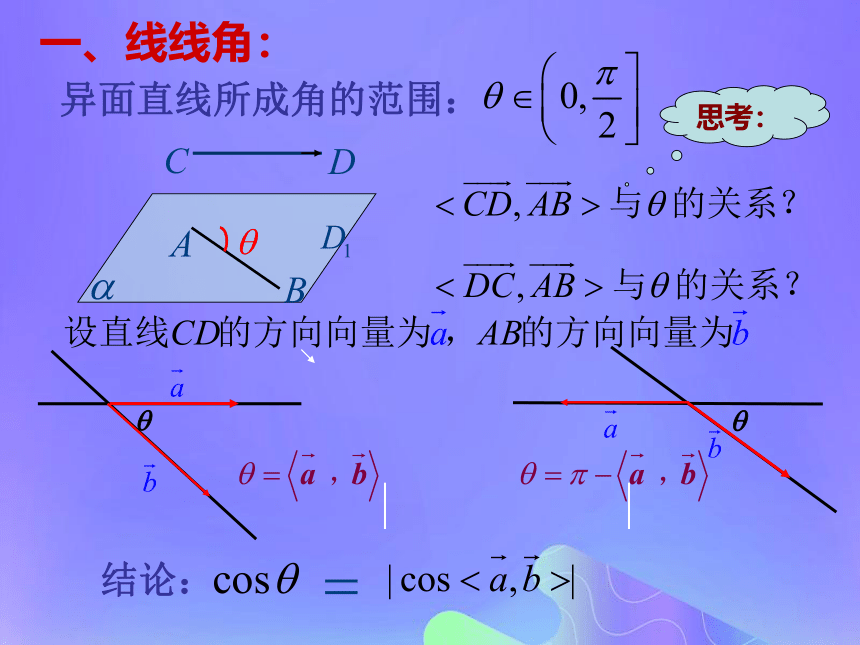
课件16张PPT。3.2.3空间的角的计算空间的角:线线角、线面角、面面角。 空间的角最终都可以转化为两相交直线所成的角。因此我们可以考虑通过两个向量的夹角去求这些空间角。异面直线所成角的范围: 思考:结论:一、线线角:所以 与 所成角的余弦值为解:以点C为坐标原点建立空间直角坐标
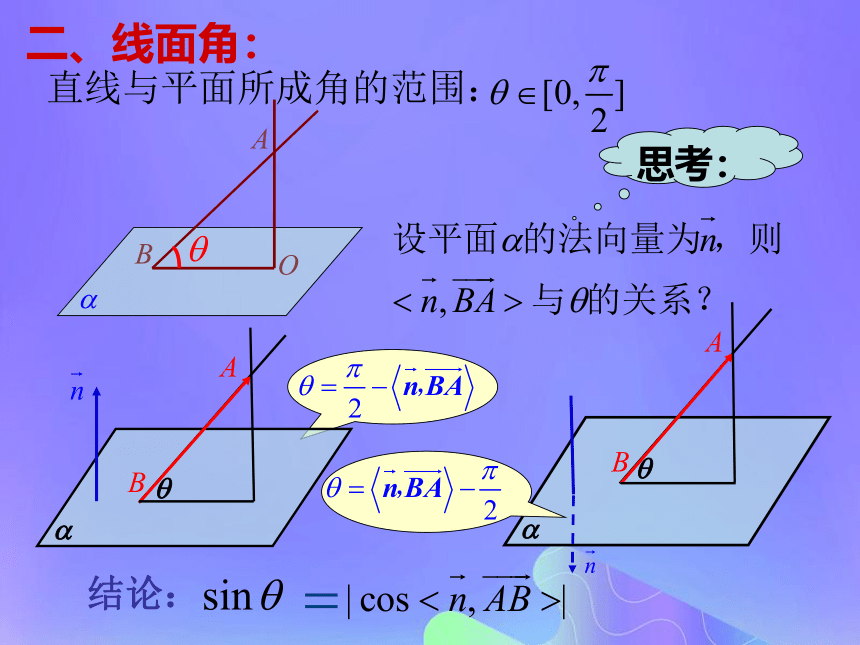
系 ,如图所示,设 则: 所以:例一:练习:在长方体 中,简解:直线与平面所成角的范围: 思考:结论:二、线面角:简解:所以~~~~练习:
xyz设正方体棱长为1,将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图,设二面角 的大小为 ,其中DCBA三、面面角:①方向向量法:二面角的范围: 例三:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处。从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 。求库底与水坝所成二面角的余弦值。 解:如图,化为向量问题根据向量的加法法则有于是,得设向量 与 的夹角为 , 就是库底与水坝所成的二面角。因此所以所以库底与水坝所成二面角的余弦值为三、面面角:二面角的范围:②法向量法注意法向量的方向:
一进一出,二面角等于法向量夹角;
同进同出,二面角等于法向量夹角的补角设平面用空间向量解决立体几何问题的“三步曲”。 (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题; (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)
(进行向量运算)(回到图形问题)
点拨:1、如果平面的一条斜线与它在这个平面上的射影的方向向量分别是 n1=(1,0,1), n2 =(0,1,1),那么这条斜线与平面所成的角是______ .2、已知两平面的法向量分别m=(0,1,0),n=(0,1,1),则两平面所成的钝二面角为______ .3. 三棱锥P-ABC PA⊥ABC,PA=AB=AC,
,E为PC中点 ,则PA与BE所成角的余弦值为_________ .
课堂练习小结:1.异面直线所成角: 2.直线与平面所成角: DCBA3.二面角:一进一出,二面角等于法向量的夹角;
同进同出,二面角等于法向量夹角的补角。
系 ,如图所示,设 则: 所以:例一:练习:在长方体 中,简解:直线与平面所成角的范围: 思考:结论:二、线面角:简解:所以~~~~练习:
xyz设正方体棱长为1,将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图,设二面角 的大小为 ,其中DCBA三、面面角:①方向向量法:二面角的范围: 例三:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处。从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 。求库底与水坝所成二面角的余弦值。 解:如图,化为向量问题根据向量的加法法则有于是,得设向量 与 的夹角为 , 就是库底与水坝所成的二面角。因此所以所以库底与水坝所成二面角的余弦值为三、面面角:二面角的范围:②法向量法注意法向量的方向:
一进一出,二面角等于法向量夹角;
同进同出,二面角等于法向量夹角的补角设平面用空间向量解决立体几何问题的“三步曲”。 (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题; (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)
(进行向量运算)(回到图形问题)
点拨:1、如果平面的一条斜线与它在这个平面上的射影的方向向量分别是 n1=(1,0,1), n2 =(0,1,1),那么这条斜线与平面所成的角是______ .2、已知两平面的法向量分别m=(0,1,0),n=(0,1,1),则两平面所成的钝二面角为______ .3. 三棱锥P-ABC PA⊥ABC,PA=AB=AC,
,E为PC中点 ,则PA与BE所成角的余弦值为_________ .
课堂练习小结:1.异面直线所成角: 2.直线与平面所成角: DCBA3.二面角:一进一出,二面角等于法向量的夹角;
同进同出,二面角等于法向量夹角的补角。
