总复习 转化 课件(共39张PPT)
文档属性
| 名称 | 总复习 转化 课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-09 21:17:22 | ||
图片预览




文档简介
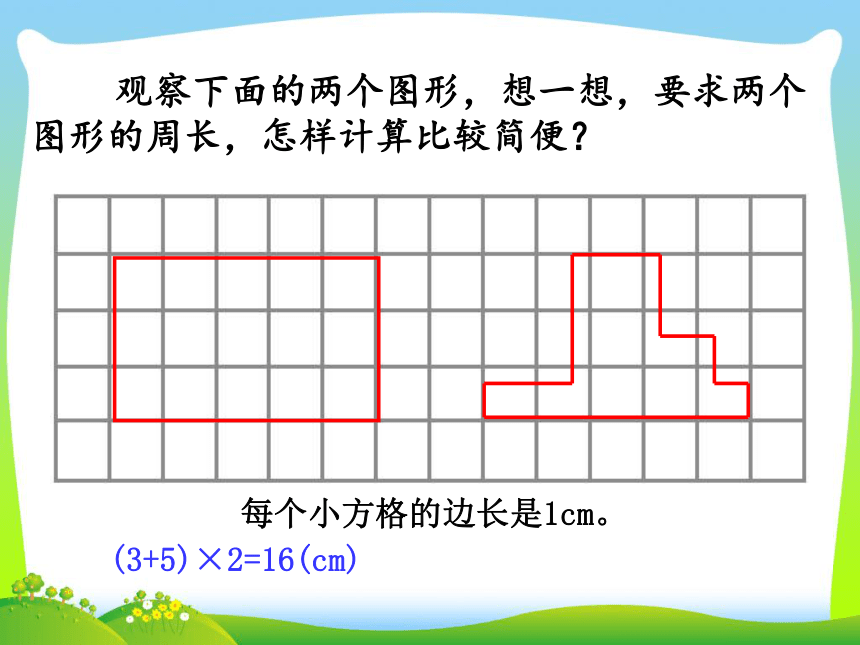
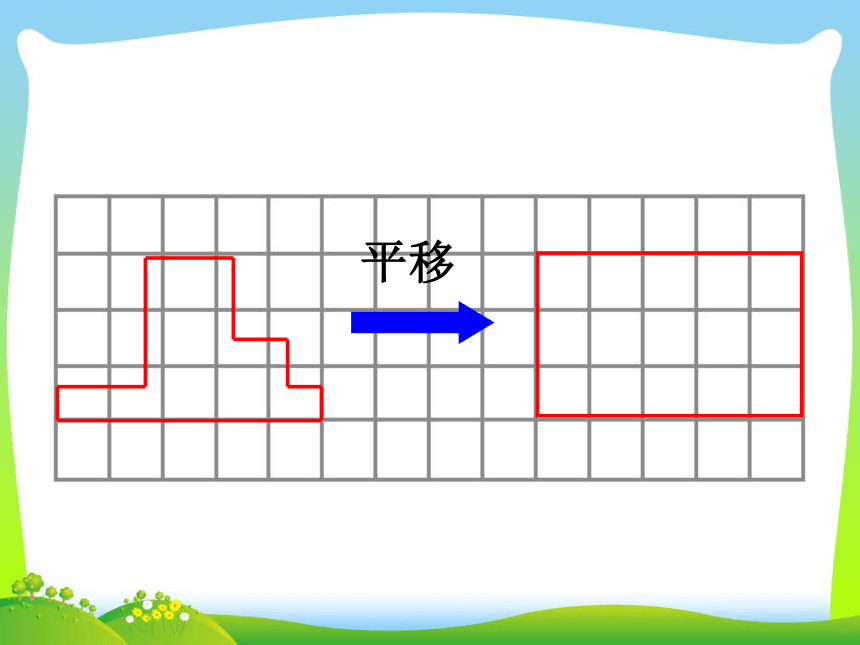
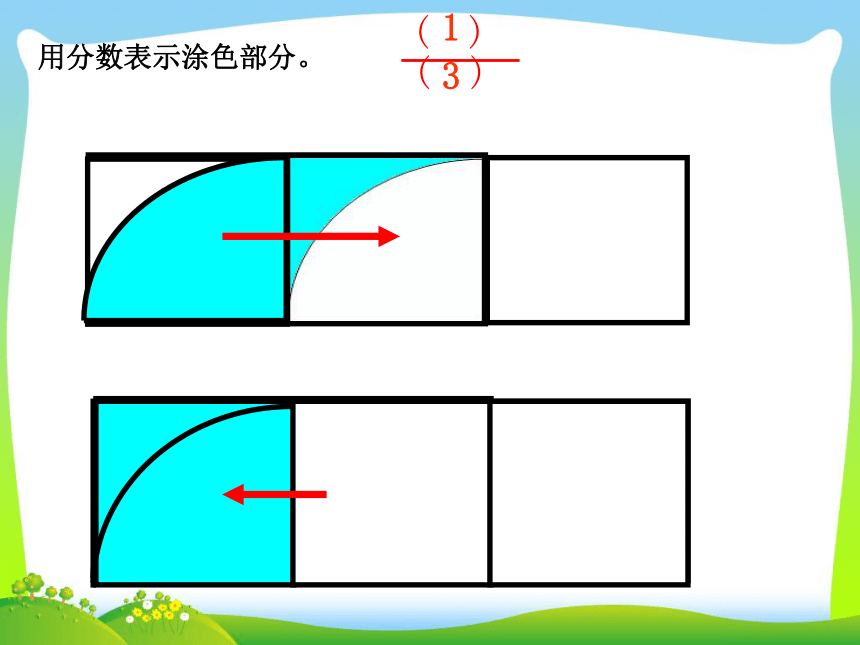
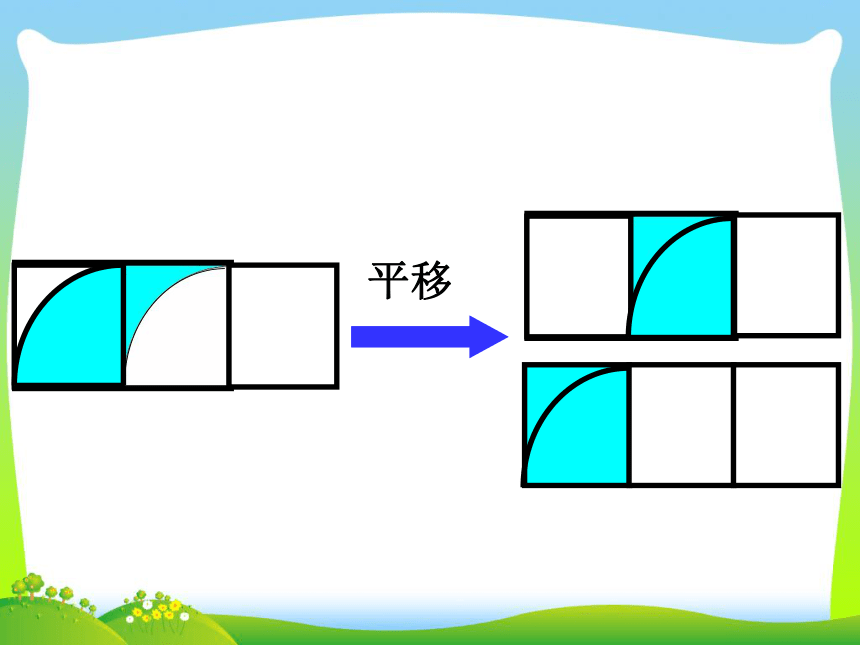
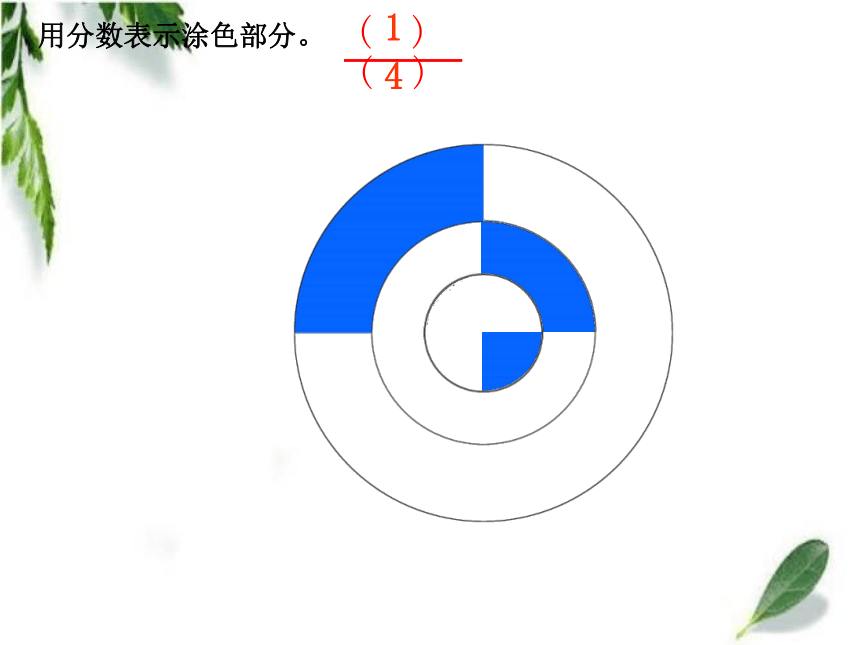
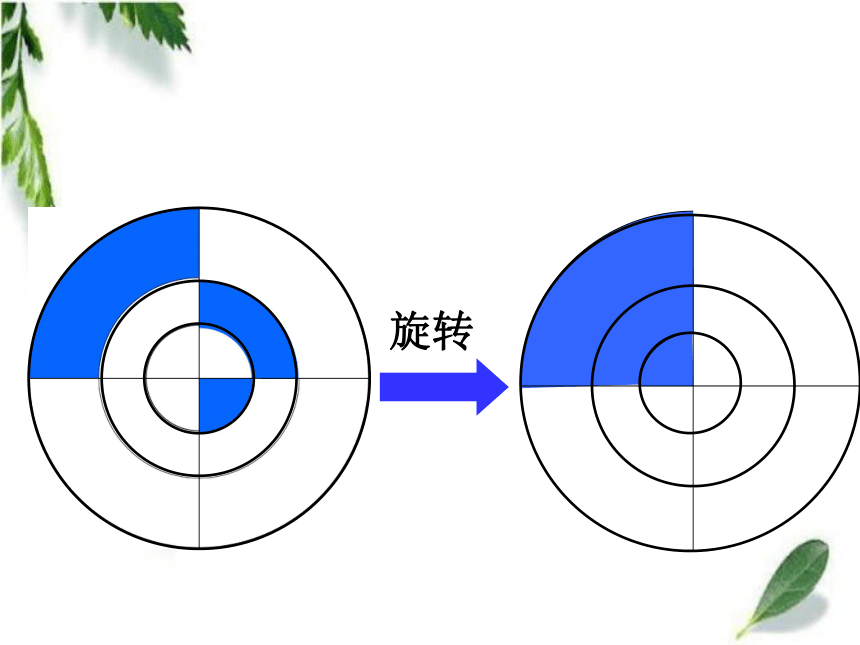
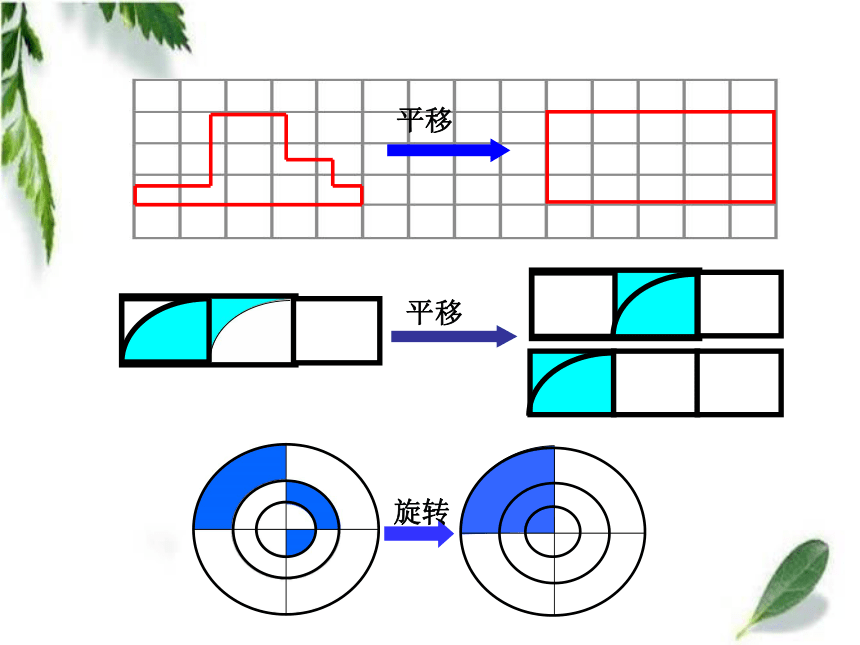
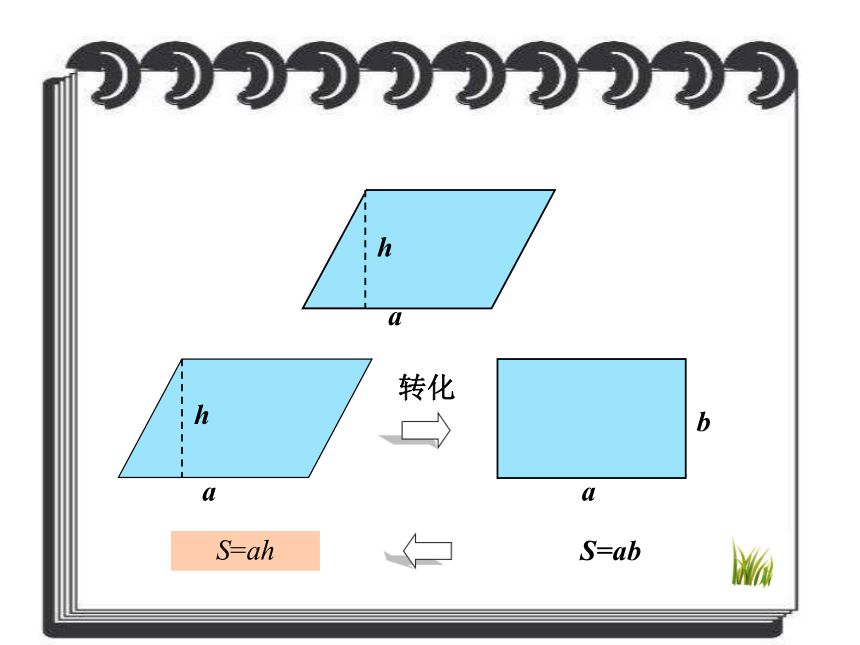
课件39张PPT。转化——解决问题的策略与方法(一)青岛版教材(五·四)学制小学数学第十册总复习 观察下面的两个图形,想一想,要求两个图形的周长,怎样计算比较简便? 每个小方格的边长是1cm。(3+5)×2=16(cm)用分数表示涂色部分。用分数表示涂色部分。哪些地方用到了转化?S=ɑbɑhS=ɑh转化ɑhS=ɑhS=ɑh÷2转化ɑhb转化S= (ɑ+b)hS=(ɑ+b)h÷2 转化S=ɑbS =πr2 V = S h底面积高圆柱的体积长方体的体积=底面积 × 高2.5×0. 4=2.5×0.4一位小数一位小数两位小数11 0 0.算一算=2.4土豆的体积:
450-200=250(mL)
250mL=250cm3 排水法排沙法 在50米的小路一边植树,每隔10米栽一棵树(两端都栽),一共需要多少棵树苗? 间隔数=50÷10=5棵数=6 在全长1000米的烟台市大路的一边植树,每隔10米栽一棵树(两端都栽),一共需要多少棵树苗? 间隔数=1000÷10=100棵数=100+1=101(两端都栽)棵数=间隔数+1天下难事,必作于易;天下大事,必作于细。+++数形结合数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
刘徽(约公元225年—295年),汉族,山东邹平县人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。 用“以盈补虚”的方法,研究了三角形和梯形的面积 高斯是近代数学奠基者之一,高斯被认为是历史上最重要的数学家之一,并享有“数学王子”之称。 用转化的策略解题 1+2+3+4+5+……+97+98+99+100=5050101×50用转化的方法测灯泡的体积 爱迪生是人类历史上第一个利用大量生产原则和电气工程研究的实验室来进行从事发明专利而对世界产生重大深远影响的人。 解题时,往往不对问题进行正面的攻击,而是不断地将它变形,直至把它转化为已经能解决的问题。
——匈牙利数学家路莎·彼得 司马光急中生智,砸破水缸,救出同伴。能吃的鱼捕鱼的方法知识获取知识
的方法
450-200=250(mL)
250mL=250cm3 排水法排沙法 在50米的小路一边植树,每隔10米栽一棵树(两端都栽),一共需要多少棵树苗? 间隔数=50÷10=5棵数=6 在全长1000米的烟台市大路的一边植树,每隔10米栽一棵树(两端都栽),一共需要多少棵树苗? 间隔数=1000÷10=100棵数=100+1=101(两端都栽)棵数=间隔数+1天下难事,必作于易;天下大事,必作于细。+++数形结合数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
刘徽(约公元225年—295年),汉族,山东邹平县人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。 用“以盈补虚”的方法,研究了三角形和梯形的面积 高斯是近代数学奠基者之一,高斯被认为是历史上最重要的数学家之一,并享有“数学王子”之称。 用转化的策略解题 1+2+3+4+5+……+97+98+99+100=5050101×50用转化的方法测灯泡的体积 爱迪生是人类历史上第一个利用大量生产原则和电气工程研究的实验室来进行从事发明专利而对世界产生重大深远影响的人。 解题时,往往不对问题进行正面的攻击,而是不断地将它变形,直至把它转化为已经能解决的问题。
——匈牙利数学家路莎·彼得 司马光急中生智,砸破水缸,救出同伴。能吃的鱼捕鱼的方法知识获取知识
的方法
