青岛版九下数学5.3二次函数课件(共23张PPT)
文档属性
| 名称 | 青岛版九下数学5.3二次函数课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 29.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-09 00:00:00 | ||
图片预览






文档简介
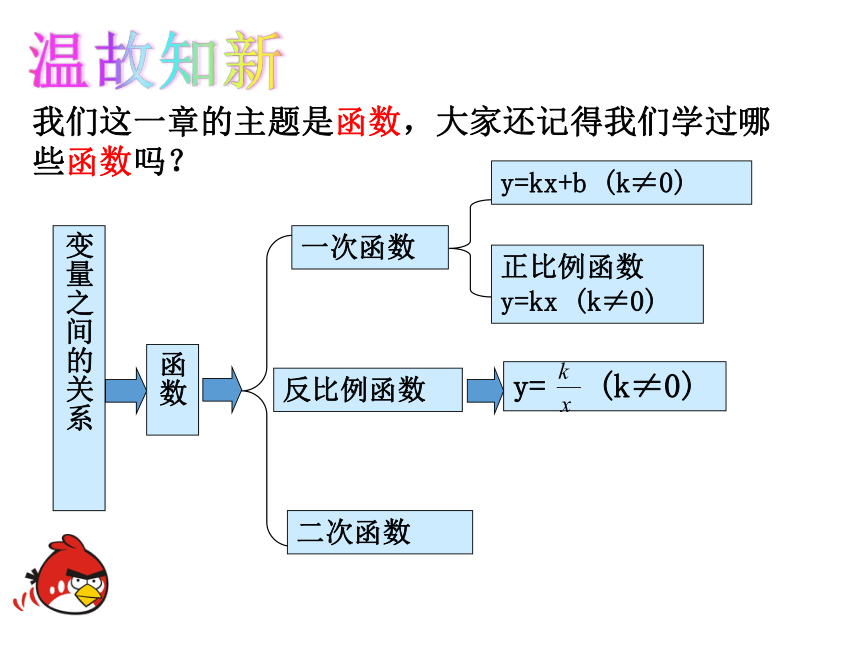
我们这一章的主题是函数,大家还记得我们学过哪些函数吗?
二次函数
将下列函数进行分类
一次函数:
反比例函数:
其他:
?
学校想用20米长的篱笆围成一个矩形花园,怎样围才能使花园的面积最大?
1.理解二次函数的概念
2.掌握二次函数的一般形式
3.会根据实际问题列出二次函数表达式
学习目标
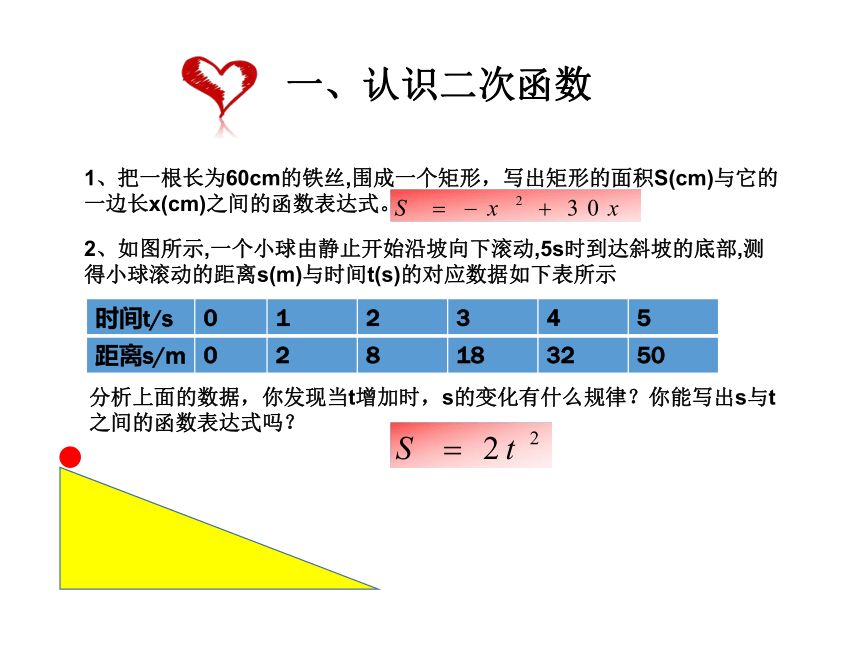
1、把一根长为60cm的铁丝,围成一个矩形,写出矩形的面积S(cm)与它的一边长x(cm)之间的函数表达式。
2、如图所示,一个小球由静止开始沿坡向下滚动,5s时到达斜坡的底部,测得小球滚动的距离s(m)与时间t(s)的对应数据如下表所示
分析上面的数据,你发现当t增加时,s的变化有什么规律?你能写出s与t之间的函数表达式吗?
时间t/s 0 1 2 3 4 5
距离s/m 0 2 8 18 32 50
3、某企业去年的产值为1200万元。该企业年产值平均每年的增长率为x,你能写出明年该企业年产值y(万元)与x之间的函数表达式吗?
今年产值:1200(1+x)
明年产值:1200(1+x)(1+x)
=1200(1+x)?
=1200x?+2400x+1200
上述三个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax?+bx+c 的形式.
(a,b,c是常数, )
a≠0
你能根据他们的共同特点写出这种函数的一般形式吗
为什么a≠0呢?
一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数,其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
你能根据二次函数的定义说出这三个函数表达式中的二次项系数、一次项系数和常数项吗?
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
1、下列函数中是二次函数的是( )
2、下列函数中是二次函数的是( )
A
C
D
B
A
C
2.写出二次函数的二次项系数、一次项系数和常数项:
2
-4
3
函数解析式 二次项系数 一次项系数 常数项
y=2(x-1)?+1
(2)含有自变量的代数式是整式
(3)自变量的最高次数为2
(4)
二次项系数不为0
(1)要判断一个函数是否是二次函数,往往需要化简整理后再下结论(整理成一般形式)
你能分别说出前面三个问题中自变量的取值范围吗?
二次函数y=ax?+bx+c的自变量可以取值的范围是全体实数
但在具体问题中,还要结合实际背景确定自变量的取值范围
1、矩形的面积S(cm)与它的一边长x(cm)之间的函数表达式。
3、企业年产值y(万元)与x之间的函数表达式
2、小球运动的距离与时间之间的关系
15
x
如图,从半径为15的圆形铁片上,挖去一个半径为x的圆。写出剩余部分的面积y与x之间的函数表达式,并指出自变量x可以取值的范围
原来圆形铁片的面积:
挖去部分的面积:
剩余部分的面积为:
因为小圆在大圆的内部,所以自变量x的取值范围是:
(1)y=3(x-1)?+1;
(是)
(否)
(3) s=3-2t?.
(5)y=(x+3)?-x?.
(6) y= x?+x?+25
(4)y=2?+2x
(是)
(否)
(否)
(否)
1、下列函数中,哪些是二次函数?
1、正方体的六个面是全等的正方形,设正方体的棱长为
x ,表面积为 y ,则 y 关于x 的关系式为____.
y=6x2
2、已知正方形的边长是3,当边长增加x时,面积增加y,写出y与x之间的函数表达式。
3、某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数表达式为
1、函数 (其中a,b,c是常数),当a,b,c满足什么条件时
(1)是二次函数?
(2)是一次函数?
(3)是正比例函数?
解:
3、函数 y=(m-n)x2+ mx+n 是二次函数的条件
是( )
A、m,n是常数,且m≠0 B、m,n是常数,且n≠0
C、m,n是常数,且m≠n D、m,n为任何实数
C
C
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx (a≠0,b≠0,c=0).
2.判断一个函数为二次函数的方法与步骤:
(1)先将函数进行整理,使其右边是含自变量的代数式,左边是因变量;
(2)判别含自变量的代数式是否为整式
(3)判别含自变量的项的最高次数是否为2;
(4)判别二次项的系数是否为0。
二次函数
将下列函数进行分类
一次函数:
反比例函数:
其他:
?
学校想用20米长的篱笆围成一个矩形花园,怎样围才能使花园的面积最大?
1.理解二次函数的概念
2.掌握二次函数的一般形式
3.会根据实际问题列出二次函数表达式
学习目标
1、把一根长为60cm的铁丝,围成一个矩形,写出矩形的面积S(cm)与它的一边长x(cm)之间的函数表达式。
2、如图所示,一个小球由静止开始沿坡向下滚动,5s时到达斜坡的底部,测得小球滚动的距离s(m)与时间t(s)的对应数据如下表所示
分析上面的数据,你发现当t增加时,s的变化有什么规律?你能写出s与t之间的函数表达式吗?
时间t/s 0 1 2 3 4 5
距离s/m 0 2 8 18 32 50
3、某企业去年的产值为1200万元。该企业年产值平均每年的增长率为x,你能写出明年该企业年产值y(万元)与x之间的函数表达式吗?
今年产值:1200(1+x)
明年产值:1200(1+x)(1+x)
=1200(1+x)?
=1200x?+2400x+1200
上述三个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax?+bx+c 的形式.
(a,b,c是常数, )
a≠0
你能根据他们的共同特点写出这种函数的一般形式吗
为什么a≠0呢?
一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数,其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
你能根据二次函数的定义说出这三个函数表达式中的二次项系数、一次项系数和常数项吗?
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
1、下列函数中是二次函数的是( )
2、下列函数中是二次函数的是( )
A
C
D
B
A
C
2.写出二次函数的二次项系数、一次项系数和常数项:
2
-4
3
函数解析式 二次项系数 一次项系数 常数项
y=2(x-1)?+1
(2)含有自变量的代数式是整式
(3)自变量的最高次数为2
(4)
二次项系数不为0
(1)要判断一个函数是否是二次函数,往往需要化简整理后再下结论(整理成一般形式)
你能分别说出前面三个问题中自变量的取值范围吗?
二次函数y=ax?+bx+c的自变量可以取值的范围是全体实数
但在具体问题中,还要结合实际背景确定自变量的取值范围
1、矩形的面积S(cm)与它的一边长x(cm)之间的函数表达式。
3、企业年产值y(万元)与x之间的函数表达式
2、小球运动的距离与时间之间的关系
15
x
如图,从半径为15的圆形铁片上,挖去一个半径为x的圆。写出剩余部分的面积y与x之间的函数表达式,并指出自变量x可以取值的范围
原来圆形铁片的面积:
挖去部分的面积:
剩余部分的面积为:
因为小圆在大圆的内部,所以自变量x的取值范围是:
(1)y=3(x-1)?+1;
(是)
(否)
(3) s=3-2t?.
(5)y=(x+3)?-x?.
(6) y= x?+x?+25
(4)y=2?+2x
(是)
(否)
(否)
(否)
1、下列函数中,哪些是二次函数?
1、正方体的六个面是全等的正方形,设正方体的棱长为
x ,表面积为 y ,则 y 关于x 的关系式为____.
y=6x2
2、已知正方形的边长是3,当边长增加x时,面积增加y,写出y与x之间的函数表达式。
3、某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数表达式为
1、函数 (其中a,b,c是常数),当a,b,c满足什么条件时
(1)是二次函数?
(2)是一次函数?
(3)是正比例函数?
解:
3、函数 y=(m-n)x2+ mx+n 是二次函数的条件
是( )
A、m,n是常数,且m≠0 B、m,n是常数,且n≠0
C、m,n是常数,且m≠n D、m,n为任何实数
C
C
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx (a≠0,b≠0,c=0).
2.判断一个函数为二次函数的方法与步骤:
(1)先将函数进行整理,使其右边是含自变量的代数式,左边是因变量;
(2)判别含自变量的代数式是否为整式
(3)判别含自变量的项的最高次数是否为2;
(4)判别二次项的系数是否为0。
