人教版高中数学选修2-3第一章第二节 排列组合的应用1-ppt课件(27ppt)
文档属性
| 名称 | 人教版高中数学选修2-3第一章第二节 排列组合的应用1-ppt课件(27ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-09 00:00:00 | ||
图片预览








文档简介
一、掌握优先处理元素(位置)法
二、掌握捆绑法
三、掌握插空法
四、隔板法
五、分组分配问题:
1、是否均匀;
2、是否有组别。
复习引入:
1、什么叫做从n个不同元素中取出m个元素的一个排列?
从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
2、什么叫做从n个不同元素中取出m个元素的排列数?
3、排列数的两个公式是什么?
(n,m∈N*,m≤n)
组合定义:一般地说,从 n 个不同元素中,任取 m (m≤n) 个元素并成一组,叫做从 n 个不同元素中取出 m 个元素的一个组合。
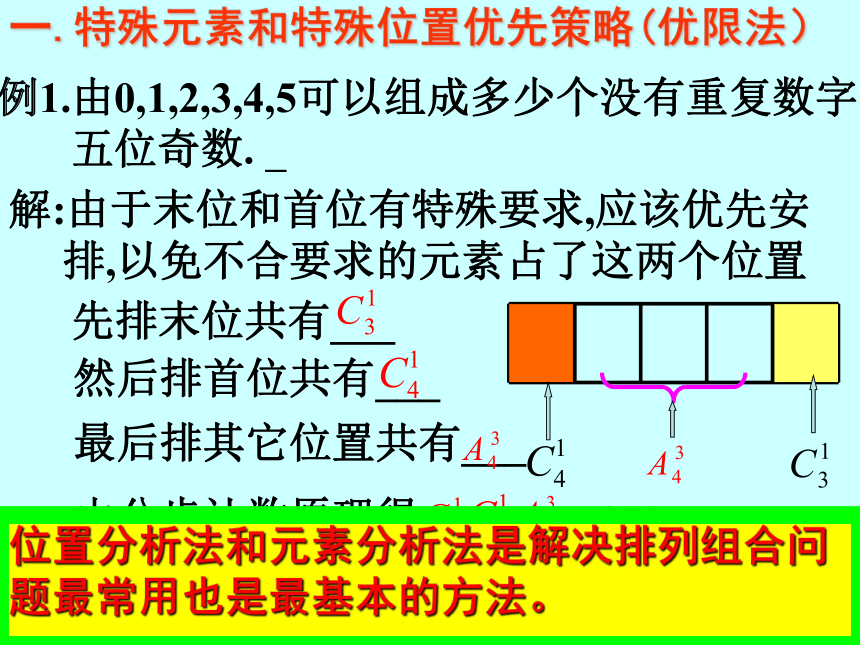
一.特殊元素和特殊位置优先策略(优限法)
例1.由0,1,2,3,4,5可以组成多少个没有重复数字
五位奇数.
解:由于末位和首位有特殊要求,应该优先安
排,以免不合要求的元素占了这两个位置
先排末位共有___
然后排首位共有___
最后排其它位置共有___
位置分析法和元素分析法是解决排列组合问题最常用也是最基本的方法。
(2)7位同学站成一排,甲、乙只能站在两端的排法共有多少种?
(1)7位同学站成一排,其中甲站在中间的位置,共有多少种不同的排法?
分析:可看作甲固定,其余全排列
例2:
(3)7位同学站成一排,甲、乙不能站在排头和排尾的排法共有多少种?
解法一:(特殊位置法)
答:共有2400种不同的排列方法。
解法二:(特殊元素法)
答:共有2400种不同的排列方法。
解法三:(排除法)
答:共有2400种不同的排列方法。
【总结归纳】
一般地,对于有限制条件的排列问题,有以下两种方法:
⑴直接计算法
排列的限制条件一般是:某些特殊位置和特殊元素. 解决的办法是“特事特办”,对于这些特殊位置和元素,实行优先考虑,即特殊元素预置法、特殊位置预置法.
⑵间接计算法
先抛开限制条件,计算出所有可能的排列数,再从中减去不合题意的排列数,特别要注意:不能遗漏,也不能重复. 即排除法.
搞清限制条件的真正含义,做针对性文章!
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
若三个女孩要站在一起,有多少种不同的排法?
二.捆绑法
若三个女孩要站在一起,四个男孩也要站在一起,有多少种不同的排法?
说一说
相邻
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
变式训练
有5盆不同的花,其中2盆牡丹花,2盆月季花,1盆杜鹃花,要求牡丹花要摆放在一起且不能放到最后,那么有多少种摆法?
捆绑法:
对于相邻问题,常常先将要相邻的元素捆绑在一起,视作为一个元素,与其余元素全排列,再松绑后它们之间进行全排列.这种方法就是捆绑法.
若三个女孩互不相邻,有多少种不同的排法?
三.插空法
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
男生、女生相间排列,有多少种不同的排法?
插空法
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
甲、乙两人的两边必须有其他人,有多少种不 同的排法?
插空法
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
某班新年联欢会原定的5个节目已排成节目单,开演前又增加了2个新节目.如果将这2个新节目插入原节目单中,且两个新节目不相邻,那么不同插法的种数为( )
30
练习题
例3.一个晚会的节目有4个舞蹈,2个相声,3个
独唱,舞蹈节目不能连续出场,则节目的出
场顺序有多少种?
解:分两步进行第一步排2个相声和3个独唱共
有 种,
插空法:
对于不相邻问题,先将其余元素全排列,再将这些不相邻的元素插入空挡中,这种方法就是插空法.
四.元素相同问题隔板策略
例7.有10个运动员名额,在分给7个班,每
班至少一个,有多少种分配方案?
解:因为10个名额没有差别,把它们排成
一排。相邻名额之间形成9个空隙。
在9个空档中选6个位置插个隔板,
可把名额分成7份,对应地分给7个
班级,每一种插板方法对应一种分法
共有___________种分法。
将n个相同的元素分成m份(n,m为正整数),每份至少一个元素,可以用 块隔板,插入n个元素排成一排的 个空隙中,所有分法数为
m-1
n-1
练习题
10个相同的球装5个盒中,每盒至少一个,有多少装法?
课堂练习:
2、4个学生和3个老师排成一排照相,老师不能排两端,且老师必须排在一起的不同排法种数是( )
A . B . C . D .
3、计划展出10幅不同的画,其中1幅水彩画,4幅油画, 5幅国画,排成一行陈列,要求同一品种的画必须连在一起,那么不同的陈列方式有( )
1、有6位教师去听同时要上的4节课,每位教师可任选其中一节课,则不同的听法种数是( )
A 360 B 64 C 46 D 44
4、在7名运动员中选出4名组成接力队,参加4×100米接力赛,那么甲、乙两人都不跑中间两棒的安排方法有多少种?
5.一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?
课堂小结:
基本的解题方法:
⑴ 有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);
⑵ 某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
⑶ 某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
⑷ 在处理排列问题时,一般可采用直接和间接两种思维形式,从而寻求有效的解题途径,这是学好排列问题的根基.
课后作业
复习“排列组合”的课本内容;
完成“非常学案活页综合测评一”第十二章测试卷;
提前预习“二项式定理”课本内容。
二、掌握捆绑法
三、掌握插空法
四、隔板法
五、分组分配问题:
1、是否均匀;
2、是否有组别。
复习引入:
1、什么叫做从n个不同元素中取出m个元素的一个排列?
从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
2、什么叫做从n个不同元素中取出m个元素的排列数?
3、排列数的两个公式是什么?
(n,m∈N*,m≤n)
组合定义:一般地说,从 n 个不同元素中,任取 m (m≤n) 个元素并成一组,叫做从 n 个不同元素中取出 m 个元素的一个组合。
一.特殊元素和特殊位置优先策略(优限法)
例1.由0,1,2,3,4,5可以组成多少个没有重复数字
五位奇数.
解:由于末位和首位有特殊要求,应该优先安
排,以免不合要求的元素占了这两个位置
先排末位共有___
然后排首位共有___
最后排其它位置共有___
位置分析法和元素分析法是解决排列组合问题最常用也是最基本的方法。
(2)7位同学站成一排,甲、乙只能站在两端的排法共有多少种?
(1)7位同学站成一排,其中甲站在中间的位置,共有多少种不同的排法?
分析:可看作甲固定,其余全排列
例2:
(3)7位同学站成一排,甲、乙不能站在排头和排尾的排法共有多少种?
解法一:(特殊位置法)
答:共有2400种不同的排列方法。
解法二:(特殊元素法)
答:共有2400种不同的排列方法。
解法三:(排除法)
答:共有2400种不同的排列方法。
【总结归纳】
一般地,对于有限制条件的排列问题,有以下两种方法:
⑴直接计算法
排列的限制条件一般是:某些特殊位置和特殊元素. 解决的办法是“特事特办”,对于这些特殊位置和元素,实行优先考虑,即特殊元素预置法、特殊位置预置法.
⑵间接计算法
先抛开限制条件,计算出所有可能的排列数,再从中减去不合题意的排列数,特别要注意:不能遗漏,也不能重复. 即排除法.
搞清限制条件的真正含义,做针对性文章!
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
若三个女孩要站在一起,有多少种不同的排法?
二.捆绑法
若三个女孩要站在一起,四个男孩也要站在一起,有多少种不同的排法?
说一说
相邻
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
变式训练
有5盆不同的花,其中2盆牡丹花,2盆月季花,1盆杜鹃花,要求牡丹花要摆放在一起且不能放到最后,那么有多少种摆法?
捆绑法:
对于相邻问题,常常先将要相邻的元素捆绑在一起,视作为一个元素,与其余元素全排列,再松绑后它们之间进行全排列.这种方法就是捆绑法.
若三个女孩互不相邻,有多少种不同的排法?
三.插空法
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
男生、女生相间排列,有多少种不同的排法?
插空法
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
甲、乙两人的两边必须有其他人,有多少种不 同的排法?
插空法
例2:七个家庭一起外出旅游,若其中四家是一个男孩,三家是一个女孩,现将这七个小孩站成一排照相留念。
某班新年联欢会原定的5个节目已排成节目单,开演前又增加了2个新节目.如果将这2个新节目插入原节目单中,且两个新节目不相邻,那么不同插法的种数为( )
30
练习题
例3.一个晚会的节目有4个舞蹈,2个相声,3个
独唱,舞蹈节目不能连续出场,则节目的出
场顺序有多少种?
解:分两步进行第一步排2个相声和3个独唱共
有 种,
插空法:
对于不相邻问题,先将其余元素全排列,再将这些不相邻的元素插入空挡中,这种方法就是插空法.
四.元素相同问题隔板策略
例7.有10个运动员名额,在分给7个班,每
班至少一个,有多少种分配方案?
解:因为10个名额没有差别,把它们排成
一排。相邻名额之间形成9个空隙。
在9个空档中选6个位置插个隔板,
可把名额分成7份,对应地分给7个
班级,每一种插板方法对应一种分法
共有___________种分法。
将n个相同的元素分成m份(n,m为正整数),每份至少一个元素,可以用 块隔板,插入n个元素排成一排的 个空隙中,所有分法数为
m-1
n-1
练习题
10个相同的球装5个盒中,每盒至少一个,有多少装法?
课堂练习:
2、4个学生和3个老师排成一排照相,老师不能排两端,且老师必须排在一起的不同排法种数是( )
A . B . C . D .
3、计划展出10幅不同的画,其中1幅水彩画,4幅油画, 5幅国画,排成一行陈列,要求同一品种的画必须连在一起,那么不同的陈列方式有( )
1、有6位教师去听同时要上的4节课,每位教师可任选其中一节课,则不同的听法种数是( )
A 360 B 64 C 46 D 44
4、在7名运动员中选出4名组成接力队,参加4×100米接力赛,那么甲、乙两人都不跑中间两棒的安排方法有多少种?
5.一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?
课堂小结:
基本的解题方法:
⑴ 有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);
⑵ 某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
⑶ 某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
⑷ 在处理排列问题时,一般可采用直接和间接两种思维形式,从而寻求有效的解题途径,这是学好排列问题的根基.
课后作业
复习“排列组合”的课本内容;
完成“非常学案活页综合测评一”第十二章测试卷;
提前预习“二项式定理”课本内容。
