人教高中数学必修一(A版)1.2.2函数的表示法PPT课件(15ppt)
文档属性
| 名称 | 人教高中数学必修一(A版)1.2.2函数的表示法PPT课件(15ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 829.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-09 00:00:00 | ||
图片预览




文档简介
解析法,图象法,列表法.
回想函数的表示方法有哪几种?
解析法
用图象表示两个变量之间的对应关系
列出表格来表示两个变量之间的对应关系
用数学表达式表示两个变量之间的对应关系
图象法
列表法
函数的表示法
函数表示法:
函数表示法
分段函数
解析法
图像法
列表法
例2
例3
例4
1.解析法:把两个变量的函数关系用一个等式来表示,这个等式叫函数的解析表达式,简称解析式。
优点:一是简明、全面的概括了变量间的关系,二是可以通过解析式求出任意一个自变量的值所对应的函数值。
2.列表法:列出表格来表示两个变量的函数关系。
优点是:不必计算就知道自变量取某些值时函数的对应值。
国民生产总值
单位:亿元
年份 1990 1991 1992 1993
生产总值 18544.7 21665.8 26651.4 34476.7
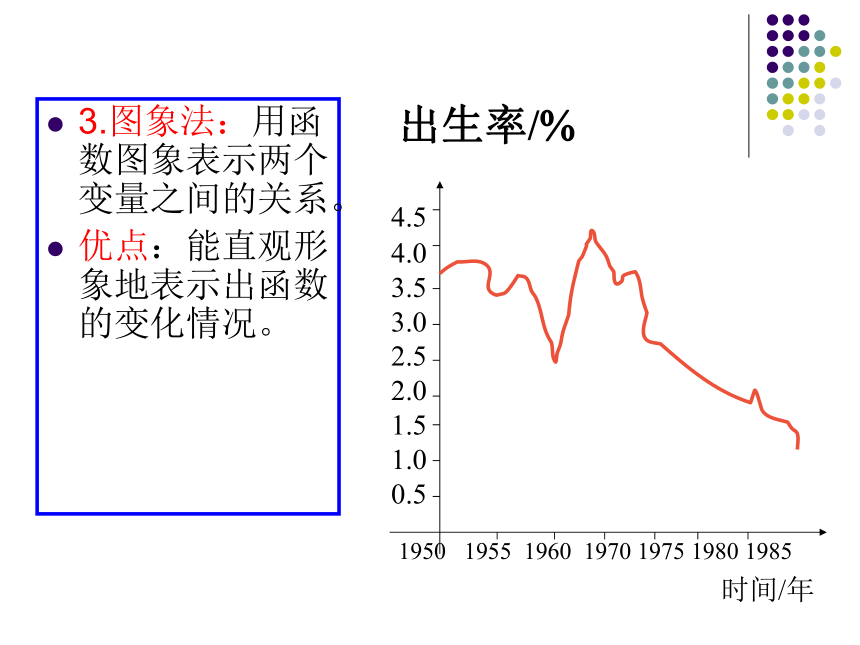
3.图象法:用函数图象表示两个变量之间的关系。
优点:能直观形象地表示出函数的变化情况。
出生率/?
解析法
图象法
列表法
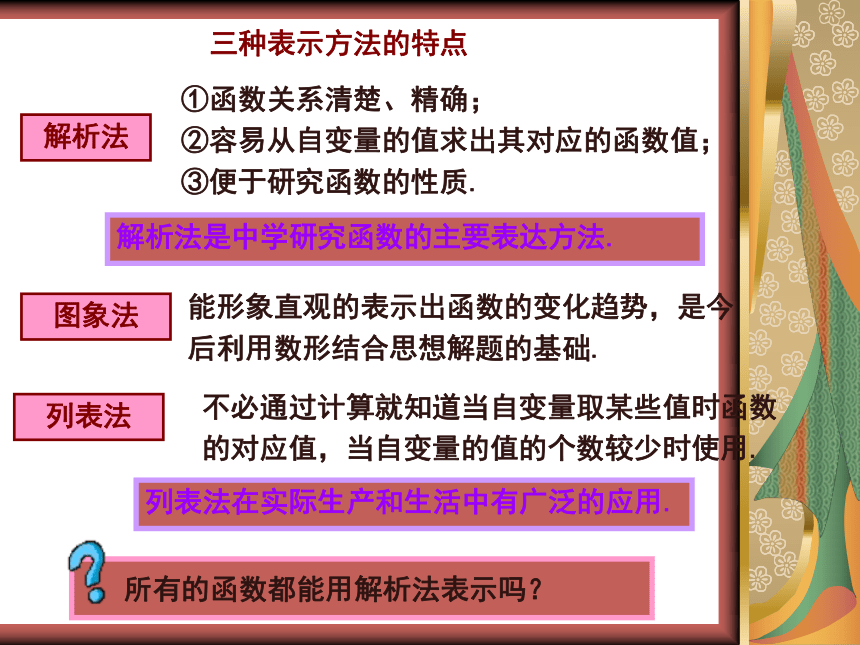
①函数关系清楚、精确;
②容易从自变量的值求出其对应的函数值;③便于研究函数的性质.
能形象直观的表示出函数的变化趋势,是今后利用数形结合思想解题的基础.
不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用.
三种表示方法的特点
解析法是中学研究函数的主要表达方法.
列表法在实际生产和生活中有广泛的应用.
例1: 在礼品盒的专卖店里,某种包装盒的单价是3元,买x 个包装盒需要y元,试用函数的三种表示法表示函数.
函数的定义域是函数存在的前提,在写函数解析式的时候,一定要写出函数的定义域.
用列表法可将函数表示为:
用图象法可将函数表示为下图:
y=3x.x∈{1,2,3,4,5}
笔记本数x 1 2 3 4 5
钱数y 3 6 9 12 15
列表、描点、连线(视其定义域决定是否连线).
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
思考
注意
例2:某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数y=f(x).
解: 这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f(x)表示为
用列表法可将函数y=f(x)表示为
用图像法可将函数y=f(x)表示为右图
y=5x, x∈{1,2,3,4,5}
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
解:由绝对值的概念,我们有
x ,x≥0,
-x ,x<0.
所以,函数y=|x|的
图象如右图所示
例3:画出函数y=|x|的图象。
例4: 某市“招手即停”公共汽车的票价按下列规则制定
(1)5公里以内(含5公里),票价2元。
(2) 5公里以上,每增加5公里,票价增加1元(不
足5公里的按5公里计算)。
如果某条路线的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。
解:设票价为y,里程为x,由题意可知,自变量的取值范围是(0,20】由“招手即停”的票价制定规则,可得函数的解析式:
0<x≤5,
5<x≤10,
10<x≤15,
15<x≤20,
2,
3,
4,
5,
分段函数
1、在定义域的不同部分上,
有不同的解析式。
2、图象不是连续的而是分段的。
本节课小结:
1、函数的表示方法:
列表法、图象法、解析法
2、函数的图象不仅可以是一段光滑的曲线还
可以是一些孤立的点还可以是若干条线段、
3、学习了用函数知识解决实际问题。
需要注意的问题
解析法必需注明定义域
分段函数是一个函数
再 见
回想函数的表示方法有哪几种?
解析法
用图象表示两个变量之间的对应关系
列出表格来表示两个变量之间的对应关系
用数学表达式表示两个变量之间的对应关系
图象法
列表法
函数的表示法
函数表示法:
函数表示法
分段函数
解析法
图像法
列表法
例2
例3
例4
1.解析法:把两个变量的函数关系用一个等式来表示,这个等式叫函数的解析表达式,简称解析式。
优点:一是简明、全面的概括了变量间的关系,二是可以通过解析式求出任意一个自变量的值所对应的函数值。
2.列表法:列出表格来表示两个变量的函数关系。
优点是:不必计算就知道自变量取某些值时函数的对应值。
国民生产总值
单位:亿元
年份 1990 1991 1992 1993
生产总值 18544.7 21665.8 26651.4 34476.7
3.图象法:用函数图象表示两个变量之间的关系。
优点:能直观形象地表示出函数的变化情况。
出生率/?
解析法
图象法
列表法
①函数关系清楚、精确;
②容易从自变量的值求出其对应的函数值;③便于研究函数的性质.
能形象直观的表示出函数的变化趋势,是今后利用数形结合思想解题的基础.
不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用.
三种表示方法的特点
解析法是中学研究函数的主要表达方法.
列表法在实际生产和生活中有广泛的应用.
例1: 在礼品盒的专卖店里,某种包装盒的单价是3元,买x 个包装盒需要y元,试用函数的三种表示法表示函数.
函数的定义域是函数存在的前提,在写函数解析式的时候,一定要写出函数的定义域.
用列表法可将函数表示为:
用图象法可将函数表示为下图:
y=3x.x∈{1,2,3,4,5}
笔记本数x 1 2 3 4 5
钱数y 3 6 9 12 15
列表、描点、连线(视其定义域决定是否连线).
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
思考
注意
例2:某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数y=f(x).
解: 这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f(x)表示为
用列表法可将函数y=f(x)表示为
用图像法可将函数y=f(x)表示为右图
y=5x, x∈{1,2,3,4,5}
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
解:由绝对值的概念,我们有
x ,x≥0,
-x ,x<0.
所以,函数y=|x|的
图象如右图所示
例3:画出函数y=|x|的图象。
例4: 某市“招手即停”公共汽车的票价按下列规则制定
(1)5公里以内(含5公里),票价2元。
(2) 5公里以上,每增加5公里,票价增加1元(不
足5公里的按5公里计算)。
如果某条路线的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。
解:设票价为y,里程为x,由题意可知,自变量的取值范围是(0,20】由“招手即停”的票价制定规则,可得函数的解析式:
0<x≤5,
5<x≤10,
10<x≤15,
15<x≤20,
2,
3,
4,
5,
分段函数
1、在定义域的不同部分上,
有不同的解析式。
2、图象不是连续的而是分段的。
本节课小结:
1、函数的表示方法:
列表法、图象法、解析法
2、函数的图象不仅可以是一段光滑的曲线还
可以是一些孤立的点还可以是若干条线段、
3、学习了用函数知识解决实际问题。
需要注意的问题
解析法必需注明定义域
分段函数是一个函数
再 见
