2018-2019学年黑龙江省哈尔滨市南岗区ff联盟七年级(上)期中数学试卷(word版含答案)
文档属性
| 名称 | 2018-2019学年黑龙江省哈尔滨市南岗区ff联盟七年级(上)期中数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-09 11:41:05 | ||
图片预览




文档简介
2018-2019学年黑龙江省哈尔滨市南岗区ff联盟七年级(上)期中数学试卷
一.选择题(每题3分,共30分)
1.(3分)下列四个式子中,是一元一次方程的是( )
A.2x﹣6 B.x﹣1=0 C.2x+y=25 D.=1
2.(3分)x=2是下列方程( )的解.
A.2x=6 B.(x﹣3)(x+2)=0
C.x2=3 D.3x﹣6=0
3.(3分)下列等式变形中,结果不正确的是( )
A.如果a=b,那么a+2b=3b
B.如果a=b,那么a﹣m=b﹣m
C.如果a=b,那么=
D.如果3x=6y﹣1,那么x=2y﹣1
4.(3分)如图,若m∥n,∠1=105°,则∠2=( )
A.55° B.60° C.65° D.75°
5.(3分)如图,图中∠1与∠2是同位角的是( )
A.(2)(3) B.(2)(3)(4) C.(1)(2)(4) D.(3)(4)
6.(3分)如图,由AD∥BC可以得到的是( )
A.∠1=∠2 B.∠3+∠4=90°
C.∠DAB+∠ABC=180° D.∠ABC+∠BCD=180°
7.(3分)如图,AB∥EF,EF∥CD,EG∥BD,则图中与∠1相等的角(除∠1外)共有( )
A.6个 B.5个 C.4个 D.2个
8.(3分)某校在举办“读书月”的活动中,将一些图书分给了七年一班的学生阅读,如果每人分3本,则剩余20本:如果每人分4本,则还缺25本.若设该校七年一班有学生x人,则下列方程正确的是( )
A.3x﹣20=24x+25 B.3x+20=4x﹣25
C.3x﹣20=4x﹣25 D.3x+20=4x+25
9.(3分)下列说法中①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③两直线平行,同旁内角互补;④直线外一点到已知直线的垂线段就是点到直线的距离,其中正确的有( )个
A.4个 B.3个 C.2个 D.1个
10.(3分)下面的程序计算,若开始输入的值为正数,最后输出的结果为131,则满足条件的x的不同值最多有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每題3分,共30分)
11.(3分)关于x的方程ax+1=4的解是x=1,则a= .
12.(3分)已知∠1与∠2是对顶角,∠2与∠3是邻补角,则∠1+∠3= .
13.(3分)若2x3﹣2k+2k=41是关于x的一元一次方程,则k= .
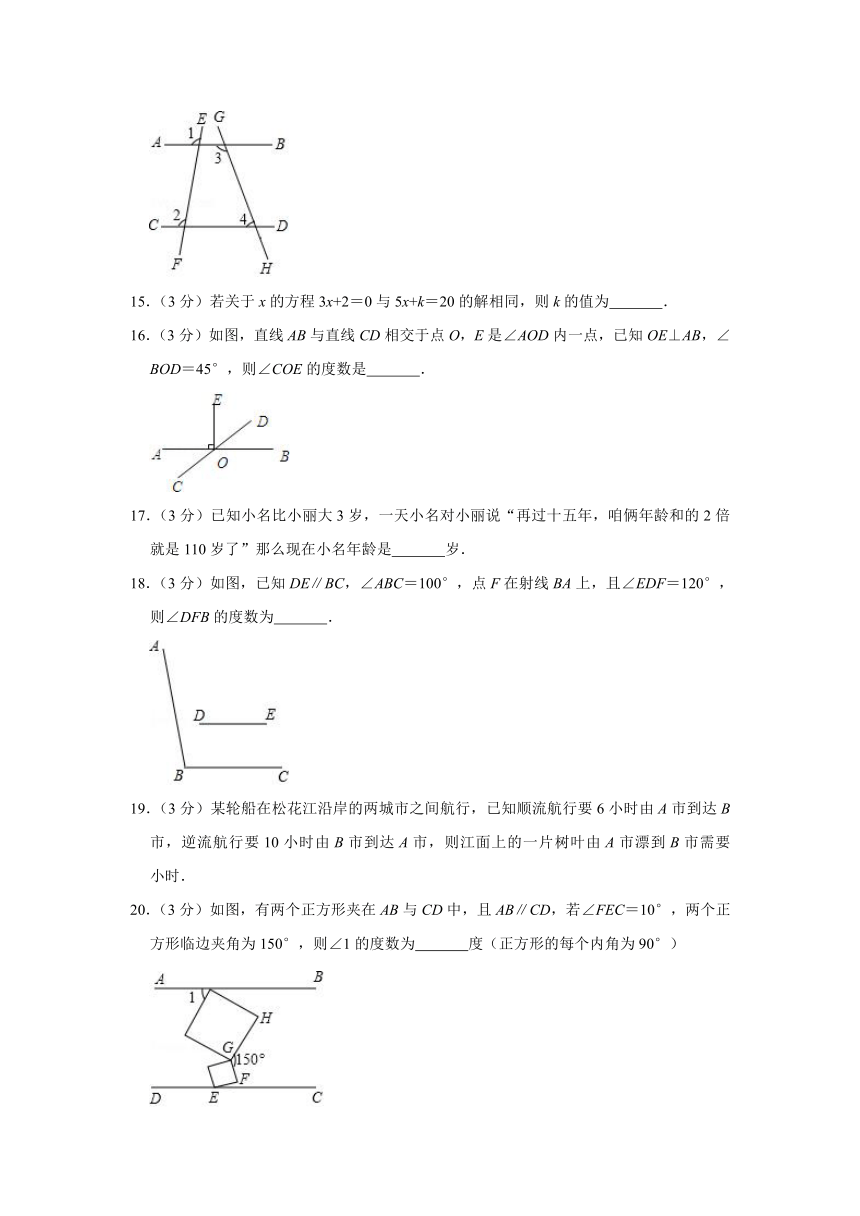
14.(3分)如图所示,∠1=100°,∠3=110°,∠2=100°,则∠4的度数为 .
15.(3分)若关于x的方程3x+2=0与5x+k=20的解相同,则k的值为 .
16.(3分)如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是 .
17.(3分)已知小名比小丽大3岁,一天小名对小丽说“再过十五年,咱俩年龄和的2倍就是110岁了”那么现在小名年龄是 岁.
18.(3分)如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为 .
19.(3分)某轮船在松花江沿岸的两城市之间航行,已知顺流航行要6小时由A市到达B市,逆流航行要10小时由B市到达A市,则江面上的一片树叶由A市漂到B市需要 小时.
20.(3分)如图,有两个正方形夹在AB与CD中,且AB∥CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为 度(正方形的每个内角为90°)
三、解答題(21題10分,22、23题各7分,24、25题各8分,26、27题各10分,共计60分
21.(10分)解方程
(1)2x+5=3x﹣3
(2)=2﹣
22.(7分)已知x=3是方程4(x﹣1)﹣mx+6=8的解,求m2+2m﹣3的值.
23.(7分)某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.两个甲种部件和三个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
24.(8分)如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
25.(8分)如图,E为DF上的点,B为AC上的点,DF∥AC,∠C=∠D,求证:∠2=∠1.
26.(10分)小明爸爸装修要粉刷断居室的墙面,在家装商场选购某品牌的乳胶漆:
规格(升/桶) 价格(元/桶)
大桶装 18 225
小桶装 5 90
小明爸估算家里的粉刷面积,若买“大桶装”,则需若干桶但还差2升;若买“小桶装”,则需多买11桶但会剩余1升,
(1)小明爸预计墙面的粉刷需要乳胶漆多少升?
(2)喜迎新年,商场进行促销:满1000减120元现金,并且该品牌商家对“小桶装”乳胶漆有“买4送1“的促销活动,小明爸打算购买“小桶装”,比促销前节省多少钱?
(3)在(2)的条件下,商家在这次乳胶漆的销售买卖中,仍可盈利25%,则小桶装乳胶漆每桶的成本是多少元?
27.(10分)已知,点A,点B分别在线段MN,PQ上∠ACB﹣∠MAC=∠CBP
(1)如图1,求证:MN∥PQ;
(2)分别过点A和点C作直线AG、CH使AG∥CH,以点B为顶点的直角∠DBI绕点B旋转,并且∠DBI的两边分别与直线CH,AG交于点F和点E,如图2试判断∠CFB、∠BEG是之间的数量关系,并证明;
(3)在(2)的条件下,若BD和AE恰好分别平分∠CBP和∠CAN,并且∠ACB=60°,求∠CFB的度数.
2018-2019学年黑龙江省哈尔滨市南岗区ff联盟七年级(上)期中数学试卷
参考答案与试题解析
一.选择题(每题3分,共30分)
1.【解答】解:A、不是等式,故不是方程,故本选项错误;
B、符合一元一次方程的定义,故本选项正确;
C、含有两个未知数,是二元一次方程,故本选项错误;
D、分母中含有未知数,是分式方程,故本选项错误.
故选:B.
2.【解答】解:将x=2代入各个方程得:
A.2x=2×2=4≠6,所以,A错误;
B.(x﹣3)(x+2)=(2﹣3)(2+2)=﹣4≠0,所以,B错误;
C.x2=22=4≠3,所以,C错误;
D.3x﹣6=3×2﹣6=0,所以,D正确;
故选:D.
3.【解答】解:A、∵a=b,
∴a+2b=b+2b,
∴a+2b=3b,正确,故本选项错误;
B、∵a=b,
∴a﹣m=b﹣m,正确,故本选项错误;
C、∵a=b,
∴ac2=bc2,正确,故本选项错误;
D、∵3x=6y﹣1,
∴两边都除以3得:x=2y﹣,错误,故本选项正确;
故选:D.
4.【解答】解:∵m∥n,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
而∠1=105°,
∴∠2=180°﹣105°=75°.
故选:D.
5.【解答】解:(1)(2)(4)中,∠1与∠2是同位角;图(3)中,∠1与∠2不是同位角,因为这两个角的边所在的直线没有一条公共边.
故选:C.
6.【解答】解:∵AD∥BC,
∴∠3=∠4,∠DAB+∠ABC=180°,
故选:C.
7.【解答】解:如图,与∠1相等的角有:∠2、∠3、∠4、∠5、∠6共5个.
故选:B.
8.【解答】解:设该校七年一班有学生x人,根据题意可得:
3x+20=4x﹣25.
故选:B.
9.【解答】解:①在同一平面内,过一点有且只有一条直线与已知直线平行;错误;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;正确;
③两直线平行,同旁内角互补;正确;
④直线外一点到已知直线的垂线段的长度就是点到直线的距离,错误;
故选:C.
10.【解答】解:若5x+1=131,即5x=130,
解得:x=26,
若5x+1=26,即5x=25,
解得:x=5,
若5x+1=5,即x=,
则满足条件的x的值是,5,26.
故选:D.
二、填空题(每題3分,共30分)
11.【解答】解:根据题意,将x=1代入ax+1=4,
得:a+1=4,
解得:a=3,
故答案为:3.
12.【解答】解:∵∠1与∠2是对顶角,
∴∠1=∠2,
又∵∠2与∠3是邻补角,
∴∠1+∠3=180°,
等角代换得∠2+∠3=180°,
故答案为:180°.
13.【解答】解:∵2x3﹣2k+2k=41是关于x的一元一次方程,
∴3﹣2k=1,
解得:k=1.
故答案为:1.
14.【解答】解:∵∠1=100°,∠2=100°,
∴∠1=∠2,
∴AB∥CD,
∴∠3+∠4=180°,
又∵∠3=110°,
∴∠4=70°,
故答案为:70°.
15.【解答】解:∵3x+2=0
∴x=
将x=代入5x+k=20中
解得:k=
16.【解答】解:∵OE⊥AB,
∴∠AOE=90°,
∵∠BOD=45°,
∴∠AOC=∠BOD=45°,
∴∠COE=∠AOE+∠AOC=90°+45°=135°.
故答案为:135°.
17.【解答】解:设现在小名年龄是x岁,
[(x+15)+(x﹣3+15)]×2=110,
解得,
x=14,
故答案为:14.
18.【解答】解:分两种情况:
①如图,延长ED交AB于G,
∵DE∥BC,
∴∠FGD=∠B=100°,
又∵∠EDF=120°,
∴∠DFB=120°﹣100°=20°;
②如图,过F作FG∥BC,
∵DE∥BC,
∴FG∥DE,
∴∠D+∠DFG=180°,∠B+∠BFG=180°,
又∵∠ABC=100°,∠EDF=120°,
∴∠BFG=80°,∠DFG=60°,
∴∠DFB=140°,
故答案为:20°或140°.
19.【解答】解:设轮A市到达B市的路程为S,江面上的一片树叶由A市漂到B市需要h小时,
=,
解得,h=30
故答案为:30.
20.【解答】解:如图,延长KH交EF的延长线于M,作MG⊥AB于G,交CD于H.
∵∠GHM=∠GFM=90°,
∴∠HMF=180°﹣150°=30°,
∵∠HMF=∠MKG+∠MEH,∠MEH=10°,
∴∠MKG=20°,
∴∠1=90°﹣20°=70°,
故答案为70.
三、解答題(21題10分,22、23题各7分,24、25题各8分,26、27题各10分,共计60分
21.【解答】解:(1)2x﹣3x=﹣3﹣5,
﹣x=﹣8,
x=8;
(2)3(3y﹣2)=24﹣4(2y﹣1),
9y﹣6=24﹣8y+4,
9y+8y=24+4+6,
17y=34,
y=2.
22.【解答】解:根据题意,将x=3代入方程4(x﹣1)mx+6=8,
得:4×(3﹣1)﹣3m+6=8,
解得:m=2,
则m2+2m﹣3
=22+2×2﹣3
=4+4﹣3
=5.
23.【解答】解:设加工的甲部件的有x人,加工的乙部件的有y人.
,由②得:12x﹣5y=0③,
①×5+③得:5x+5y+12x﹣5y=425,即17x=425,
解得x=25,
把x=25代入①解得y=60,
所以
答:加工的甲部件的有25人,加工的乙部件的有60人.
24.【解答】证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2(两直线平行,内错角相等)
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥BD(内错角相等,两直线平行)
∴∠3=∠1(两直线平行,同位角相等)
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
故答案为:两直线平行,内错角相等;BD;内错角相等,两直线平行;两直线平行,同位角相等.
25.【解答】证明:∵DF∥AC,
∴∠C=∠CEF,
又∵∠C=∠D,
∴∠CEF=∠D,
∴BD∥CE,
∴∠3=∠4,
又∵∠3=∠2,∠4=∠1,
∴∠2=∠1.
26.【解答】解:(1)设需购买“大桶装”乳胶漆x桶,则需购买“小桶装”乳胶漆(x+11)桶,
依题意,得:18x+2=5(x+11)﹣1,
解得:x=4,
∴18x+2=74.
答:小明爸预计墙面的粉刷需要乳胶漆74升.
(2)由(1)可知,需购买15桶“小桶装”乳胶漆.
∵商家对“小桶装”乳胶漆有“买4送1“的促销活动,
∴只需购买15×=12(桶),
∴比促销前可节省15×90﹣(12×90﹣120)=390(元).
答:比促销前节省390元钱.
(3)设“小桶装”乳胶漆每桶的成本是y元,
依题意,得:12×90﹣120﹣15y=15y×25%,
解得:y=51.2.
答:“小桶装”乳胶漆每桶的成本是51.2元.
27.【解答】解:(1)过C作CE∥MN,
∴∠1=∠MAC,
∵∠2=∠ACB﹣∠1,
∴∠2=∠ACB﹣∠MAC,
∵∠ACB﹣∠MAC=∠CBP,
∴∠2=∠CBP,
∴CE∥PQ,
∴MN∥PQ;
(2)过B作BR∥AG,
∵AG∥CH,
∴BR∥HF,
∴∠BEG=∠EBR,∠RBF+∠CFB=180°,
∵∠EBF=90°,
∴∠BEG=∠EBR=90°﹣∠RBF,
∴∠BEG=90°﹣∠RBF=90°﹣(180°﹣∠CFB),
∴∠CFB﹣∠BEG=90°;
(3)过E作ES∥MN,
∵MN∥PQ,
∴ES∥PQ,
∴∠NAE=∠AES,∠QBE=∠EBC,
∵BD和AE分别平分∠CBP和∠CAN,
∴∠NAE=∠EAC,∠CBD=∠DBP,
∴∠CAE=∠AES,
∵∠EBD=90°,
∴∠EBQ+∠PBD=∠EBC+∠CBD=90°,
∴∠QBE=∠EBC,
∴∠AEB=∠AES+∠BES=∠CAE+∠CBE=,
∵∠ACB=60°,
∴∠AEB=150°,
∴∠BEG=30°,
∵∠CFB﹣∠BEG=90°,
∴∠CFB=120°.
一.选择题(每题3分,共30分)
1.(3分)下列四个式子中,是一元一次方程的是( )
A.2x﹣6 B.x﹣1=0 C.2x+y=25 D.=1
2.(3分)x=2是下列方程( )的解.
A.2x=6 B.(x﹣3)(x+2)=0
C.x2=3 D.3x﹣6=0
3.(3分)下列等式变形中,结果不正确的是( )
A.如果a=b,那么a+2b=3b
B.如果a=b,那么a﹣m=b﹣m
C.如果a=b,那么=
D.如果3x=6y﹣1,那么x=2y﹣1
4.(3分)如图,若m∥n,∠1=105°,则∠2=( )
A.55° B.60° C.65° D.75°
5.(3分)如图,图中∠1与∠2是同位角的是( )
A.(2)(3) B.(2)(3)(4) C.(1)(2)(4) D.(3)(4)
6.(3分)如图,由AD∥BC可以得到的是( )
A.∠1=∠2 B.∠3+∠4=90°
C.∠DAB+∠ABC=180° D.∠ABC+∠BCD=180°
7.(3分)如图,AB∥EF,EF∥CD,EG∥BD,则图中与∠1相等的角(除∠1外)共有( )
A.6个 B.5个 C.4个 D.2个
8.(3分)某校在举办“读书月”的活动中,将一些图书分给了七年一班的学生阅读,如果每人分3本,则剩余20本:如果每人分4本,则还缺25本.若设该校七年一班有学生x人,则下列方程正确的是( )
A.3x﹣20=24x+25 B.3x+20=4x﹣25
C.3x﹣20=4x﹣25 D.3x+20=4x+25
9.(3分)下列说法中①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③两直线平行,同旁内角互补;④直线外一点到已知直线的垂线段就是点到直线的距离,其中正确的有( )个
A.4个 B.3个 C.2个 D.1个
10.(3分)下面的程序计算,若开始输入的值为正数,最后输出的结果为131,则满足条件的x的不同值最多有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每題3分,共30分)
11.(3分)关于x的方程ax+1=4的解是x=1,则a= .
12.(3分)已知∠1与∠2是对顶角,∠2与∠3是邻补角,则∠1+∠3= .
13.(3分)若2x3﹣2k+2k=41是关于x的一元一次方程,则k= .
14.(3分)如图所示,∠1=100°,∠3=110°,∠2=100°,则∠4的度数为 .
15.(3分)若关于x的方程3x+2=0与5x+k=20的解相同,则k的值为 .
16.(3分)如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是 .
17.(3分)已知小名比小丽大3岁,一天小名对小丽说“再过十五年,咱俩年龄和的2倍就是110岁了”那么现在小名年龄是 岁.
18.(3分)如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为 .
19.(3分)某轮船在松花江沿岸的两城市之间航行,已知顺流航行要6小时由A市到达B市,逆流航行要10小时由B市到达A市,则江面上的一片树叶由A市漂到B市需要 小时.
20.(3分)如图,有两个正方形夹在AB与CD中,且AB∥CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为 度(正方形的每个内角为90°)
三、解答題(21題10分,22、23题各7分,24、25题各8分,26、27题各10分,共计60分
21.(10分)解方程
(1)2x+5=3x﹣3
(2)=2﹣
22.(7分)已知x=3是方程4(x﹣1)﹣mx+6=8的解,求m2+2m﹣3的值.
23.(7分)某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.两个甲种部件和三个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
24.(8分)如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
25.(8分)如图,E为DF上的点,B为AC上的点,DF∥AC,∠C=∠D,求证:∠2=∠1.
26.(10分)小明爸爸装修要粉刷断居室的墙面,在家装商场选购某品牌的乳胶漆:
规格(升/桶) 价格(元/桶)
大桶装 18 225
小桶装 5 90
小明爸估算家里的粉刷面积,若买“大桶装”,则需若干桶但还差2升;若买“小桶装”,则需多买11桶但会剩余1升,
(1)小明爸预计墙面的粉刷需要乳胶漆多少升?
(2)喜迎新年,商场进行促销:满1000减120元现金,并且该品牌商家对“小桶装”乳胶漆有“买4送1“的促销活动,小明爸打算购买“小桶装”,比促销前节省多少钱?
(3)在(2)的条件下,商家在这次乳胶漆的销售买卖中,仍可盈利25%,则小桶装乳胶漆每桶的成本是多少元?
27.(10分)已知,点A,点B分别在线段MN,PQ上∠ACB﹣∠MAC=∠CBP
(1)如图1,求证:MN∥PQ;
(2)分别过点A和点C作直线AG、CH使AG∥CH,以点B为顶点的直角∠DBI绕点B旋转,并且∠DBI的两边分别与直线CH,AG交于点F和点E,如图2试判断∠CFB、∠BEG是之间的数量关系,并证明;
(3)在(2)的条件下,若BD和AE恰好分别平分∠CBP和∠CAN,并且∠ACB=60°,求∠CFB的度数.
2018-2019学年黑龙江省哈尔滨市南岗区ff联盟七年级(上)期中数学试卷
参考答案与试题解析
一.选择题(每题3分,共30分)
1.【解答】解:A、不是等式,故不是方程,故本选项错误;
B、符合一元一次方程的定义,故本选项正确;
C、含有两个未知数,是二元一次方程,故本选项错误;
D、分母中含有未知数,是分式方程,故本选项错误.
故选:B.
2.【解答】解:将x=2代入各个方程得:
A.2x=2×2=4≠6,所以,A错误;
B.(x﹣3)(x+2)=(2﹣3)(2+2)=﹣4≠0,所以,B错误;
C.x2=22=4≠3,所以,C错误;
D.3x﹣6=3×2﹣6=0,所以,D正确;
故选:D.
3.【解答】解:A、∵a=b,
∴a+2b=b+2b,
∴a+2b=3b,正确,故本选项错误;
B、∵a=b,
∴a﹣m=b﹣m,正确,故本选项错误;
C、∵a=b,
∴ac2=bc2,正确,故本选项错误;
D、∵3x=6y﹣1,
∴两边都除以3得:x=2y﹣,错误,故本选项正确;
故选:D.
4.【解答】解:∵m∥n,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
而∠1=105°,
∴∠2=180°﹣105°=75°.
故选:D.
5.【解答】解:(1)(2)(4)中,∠1与∠2是同位角;图(3)中,∠1与∠2不是同位角,因为这两个角的边所在的直线没有一条公共边.
故选:C.
6.【解答】解:∵AD∥BC,
∴∠3=∠4,∠DAB+∠ABC=180°,
故选:C.
7.【解答】解:如图,与∠1相等的角有:∠2、∠3、∠4、∠5、∠6共5个.
故选:B.
8.【解答】解:设该校七年一班有学生x人,根据题意可得:
3x+20=4x﹣25.
故选:B.
9.【解答】解:①在同一平面内,过一点有且只有一条直线与已知直线平行;错误;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;正确;
③两直线平行,同旁内角互补;正确;
④直线外一点到已知直线的垂线段的长度就是点到直线的距离,错误;
故选:C.
10.【解答】解:若5x+1=131,即5x=130,
解得:x=26,
若5x+1=26,即5x=25,
解得:x=5,
若5x+1=5,即x=,
则满足条件的x的值是,5,26.
故选:D.
二、填空题(每題3分,共30分)
11.【解答】解:根据题意,将x=1代入ax+1=4,
得:a+1=4,
解得:a=3,
故答案为:3.
12.【解答】解:∵∠1与∠2是对顶角,
∴∠1=∠2,
又∵∠2与∠3是邻补角,
∴∠1+∠3=180°,
等角代换得∠2+∠3=180°,
故答案为:180°.
13.【解答】解:∵2x3﹣2k+2k=41是关于x的一元一次方程,
∴3﹣2k=1,
解得:k=1.
故答案为:1.
14.【解答】解:∵∠1=100°,∠2=100°,
∴∠1=∠2,
∴AB∥CD,
∴∠3+∠4=180°,
又∵∠3=110°,
∴∠4=70°,
故答案为:70°.
15.【解答】解:∵3x+2=0
∴x=
将x=代入5x+k=20中
解得:k=
16.【解答】解:∵OE⊥AB,
∴∠AOE=90°,
∵∠BOD=45°,
∴∠AOC=∠BOD=45°,
∴∠COE=∠AOE+∠AOC=90°+45°=135°.
故答案为:135°.
17.【解答】解:设现在小名年龄是x岁,
[(x+15)+(x﹣3+15)]×2=110,
解得,
x=14,
故答案为:14.
18.【解答】解:分两种情况:
①如图,延长ED交AB于G,
∵DE∥BC,
∴∠FGD=∠B=100°,
又∵∠EDF=120°,
∴∠DFB=120°﹣100°=20°;
②如图,过F作FG∥BC,
∵DE∥BC,
∴FG∥DE,
∴∠D+∠DFG=180°,∠B+∠BFG=180°,
又∵∠ABC=100°,∠EDF=120°,
∴∠BFG=80°,∠DFG=60°,
∴∠DFB=140°,
故答案为:20°或140°.
19.【解答】解:设轮A市到达B市的路程为S,江面上的一片树叶由A市漂到B市需要h小时,
=,
解得,h=30
故答案为:30.
20.【解答】解:如图,延长KH交EF的延长线于M,作MG⊥AB于G,交CD于H.
∵∠GHM=∠GFM=90°,
∴∠HMF=180°﹣150°=30°,
∵∠HMF=∠MKG+∠MEH,∠MEH=10°,
∴∠MKG=20°,
∴∠1=90°﹣20°=70°,
故答案为70.
三、解答題(21題10分,22、23题各7分,24、25题各8分,26、27题各10分,共计60分
21.【解答】解:(1)2x﹣3x=﹣3﹣5,
﹣x=﹣8,
x=8;
(2)3(3y﹣2)=24﹣4(2y﹣1),
9y﹣6=24﹣8y+4,
9y+8y=24+4+6,
17y=34,
y=2.
22.【解答】解:根据题意,将x=3代入方程4(x﹣1)mx+6=8,
得:4×(3﹣1)﹣3m+6=8,
解得:m=2,
则m2+2m﹣3
=22+2×2﹣3
=4+4﹣3
=5.
23.【解答】解:设加工的甲部件的有x人,加工的乙部件的有y人.
,由②得:12x﹣5y=0③,
①×5+③得:5x+5y+12x﹣5y=425,即17x=425,
解得x=25,
把x=25代入①解得y=60,
所以
答:加工的甲部件的有25人,加工的乙部件的有60人.
24.【解答】证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2(两直线平行,内错角相等)
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥BD(内错角相等,两直线平行)
∴∠3=∠1(两直线平行,同位角相等)
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
故答案为:两直线平行,内错角相等;BD;内错角相等,两直线平行;两直线平行,同位角相等.
25.【解答】证明:∵DF∥AC,
∴∠C=∠CEF,
又∵∠C=∠D,
∴∠CEF=∠D,
∴BD∥CE,
∴∠3=∠4,
又∵∠3=∠2,∠4=∠1,
∴∠2=∠1.
26.【解答】解:(1)设需购买“大桶装”乳胶漆x桶,则需购买“小桶装”乳胶漆(x+11)桶,
依题意,得:18x+2=5(x+11)﹣1,
解得:x=4,
∴18x+2=74.
答:小明爸预计墙面的粉刷需要乳胶漆74升.
(2)由(1)可知,需购买15桶“小桶装”乳胶漆.
∵商家对“小桶装”乳胶漆有“买4送1“的促销活动,
∴只需购买15×=12(桶),
∴比促销前可节省15×90﹣(12×90﹣120)=390(元).
答:比促销前节省390元钱.
(3)设“小桶装”乳胶漆每桶的成本是y元,
依题意,得:12×90﹣120﹣15y=15y×25%,
解得:y=51.2.
答:“小桶装”乳胶漆每桶的成本是51.2元.
27.【解答】解:(1)过C作CE∥MN,
∴∠1=∠MAC,
∵∠2=∠ACB﹣∠1,
∴∠2=∠ACB﹣∠MAC,
∵∠ACB﹣∠MAC=∠CBP,
∴∠2=∠CBP,
∴CE∥PQ,
∴MN∥PQ;
(2)过B作BR∥AG,
∵AG∥CH,
∴BR∥HF,
∴∠BEG=∠EBR,∠RBF+∠CFB=180°,
∵∠EBF=90°,
∴∠BEG=∠EBR=90°﹣∠RBF,
∴∠BEG=90°﹣∠RBF=90°﹣(180°﹣∠CFB),
∴∠CFB﹣∠BEG=90°;
(3)过E作ES∥MN,
∵MN∥PQ,
∴ES∥PQ,
∴∠NAE=∠AES,∠QBE=∠EBC,
∵BD和AE分别平分∠CBP和∠CAN,
∴∠NAE=∠EAC,∠CBD=∠DBP,
∴∠CAE=∠AES,
∵∠EBD=90°,
∴∠EBQ+∠PBD=∠EBC+∠CBD=90°,
∴∠QBE=∠EBC,
∴∠AEB=∠AES+∠BES=∠CAE+∠CBE=,
∵∠ACB=60°,
∴∠AEB=150°,
∴∠BEG=30°,
∵∠CFB﹣∠BEG=90°,
∴∠CFB=120°.
同课章节目录
