人教版八年级数学下册 17.1勾股定理 同步测试(含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.1勾股定理 同步测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 281.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-10 00:00:00 | ||
图片预览



文档简介
17.1勾股定理
一、选择题:
1.下列各组数:①3、4、5 ②4、5、6 ③2.5、6、6.5 ④8、15、17,其中是勾股数的有( C )
A. 4组 B. 3组 C. 2组 D. 1组
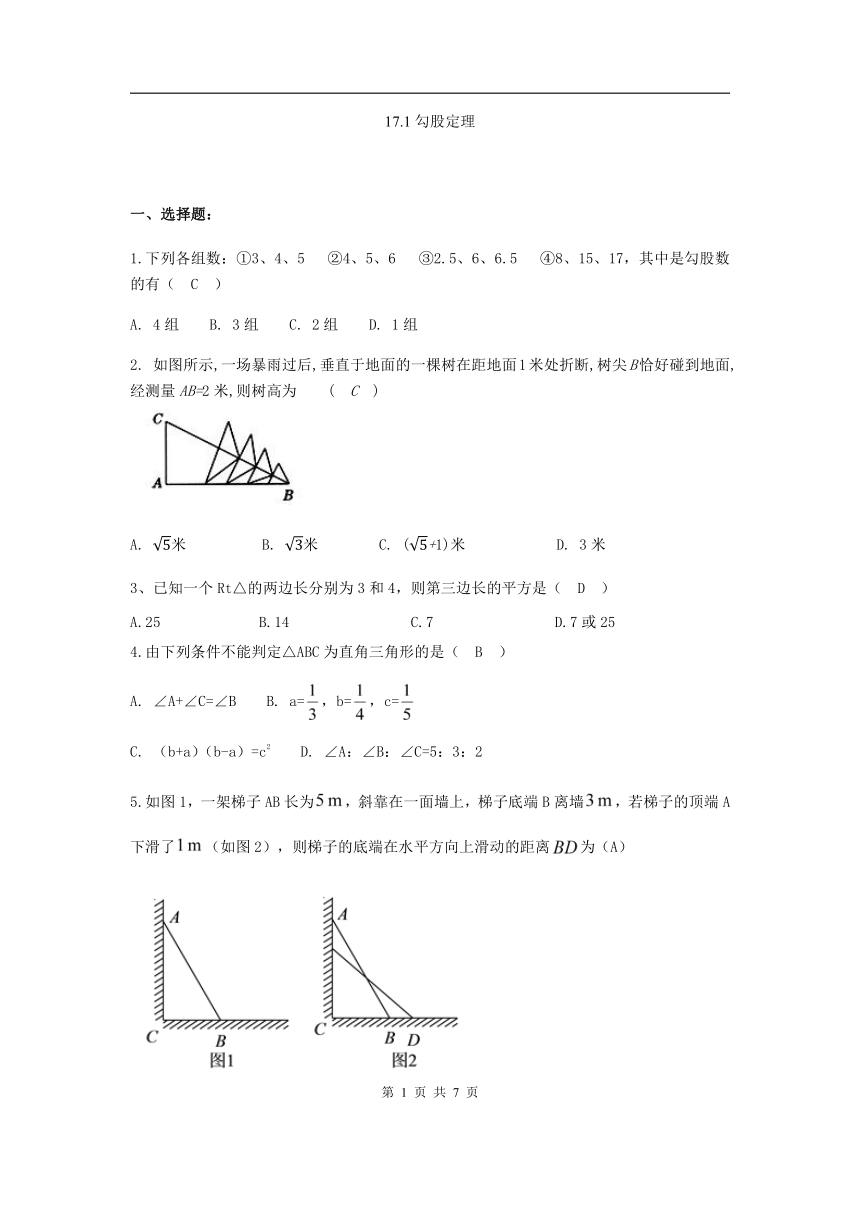
2. 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为 ( C )
?
A. 米?????B. 米????C. (+1)米??????D. 3米???????
3、已知一个Rt△的两边长分别为3和4,则第三边长的平方是( D )
A.25?? ? ?? B.14??? ???? C.7??? ???? D.7或25
4.由下列条件不能判定△ABC为直角三角形的是( B )
A. ∠A+∠C=∠B B. a=,b=,c=
C. (b+a)(b-a)=c2 D. ∠A:∠B:∠C=5:3:2
5.如图1,一架梯子AB长为,斜靠在一面墙上,梯子底端B离墙,若梯子的顶端A下滑了(如图2),则梯子的底端在水平方向上滑动的距离为(A)
A. B.大于
C.介于和之间 D.介于和之间
6.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( D )
A. 90° B. 60° C. 30° D. 45°
7.一直角三角形的三边分别为2、3、x,那么x为( C )
A.??? ? B.? C.或???? D.无法确定
8.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( C )
(A) 米 (B) 米
(C)(+1)米 (D)3米
9.直角三角形的面积为S,斜边上的中线长为d,则这个三角形周长为( C )
A. B. C. D.
10. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( A )
①②③???B. ①②④???C. ①③④??????D. ①②③④???
二、填空题
11. 已知等腰三角形的一边长为10,面积为30,该三角形的周长为 .?
【答案】10+2或20+2或20+6
12.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为 ?? m.
【答案】2.2.
(2018云南)在△ABC中,AB=,AC=5.若BC边上的高等于3,则BC边的长为 .
【答案】1或9
14.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为________.
【答案】9
15.如图,在中,,,,现将沿进行翻折,使点刚好落在上,则__________.
【答案】
16.图甲是第七届国际数学教育大会(简称ICME~7)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,那么OA1,OA2,…,OA25这些线段中有 条线段的长度为正整数.?
【答案】5
解答题
17.如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
【答案】(1)∠BAD=135°;(2)四边形ABCD的面积 2+
解析:
(1)∵∠B=90°,AB=BC=2,
∴AC= =2 ,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
(2)连接AC,如图所示:
在直角△ABC中,AC为斜边,且AB=BC=2,则AC=,
∵AD=1,CD=3,
∴AC2+CD2=AC2,
即△ACD为直角三角形,且∠ADC=90°,
四边形ABCD的面积=S△ABC+S△ACD=AB×BC+AD×AC=2+.
如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.
?
【答案】如图,过点C作CG∥AB交ED的延长
?
?线于点G,连接FG.
?∵CG∥AB,∴∠B=∠DCG,∠BED=∠DGC.
?∵BD=CD,∴△BDE≌△CDG,(AAS)
?∴DE=DG,BE=CG.
?∵∠EDF=90°,∴DF垂直平分EG,
?∴EF=FG.
?∵∠A=90°,∴∠B+∠DCF=180°-90°=90°,
?∴∠DCF+∠DCG=∠FCG=90°.
?在Rt△CFG中,CG2+CF2=FG2,
?即BE2+CF2=EF2.
19.如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.(1)求证:CD=BE;????????????????????????????????????
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
(1)证明:∵在△ABC中,AC=BC,∠C=90°,∴△ABC是等腰直角三角形,∴∠B=45°,
∵DE⊥AB,∴△BDE是等腰直角三角形,∴DE=BE.
∵AD是△ABC的角平分线,∴CD=DE,∴CD=BE;
(2)解:∵由(1)知,△BDE是等腰直角三角形,DE=BE=CD,∴DE=BE=CD=2,
∴BD===2,∴AC=BC=CD+BD=2+2;
(3)证明:∵AD是△ABC的角平分线,DE⊥AB,∴CD=DE.
在Rt△ACD与Rt△AED中,∵,∴Rt△ACD≌Rt△AED,∴AE=AC.
∵由(1)知CD=BE,∴AB=AE+BE=AC+CD.
20.如图,在△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,垂足为A,CD=1 cm,求AB的长.
解:∵在△ABC中,∠BAC=120°,∠B=30°,
∴∠C=180°-120°-30°=30°,∠DAC=120°-90°=30°,
即∠DAC=∠C,
∴CD=AD=1 cm.
在Rt△ABD中,∠B=30°,BD=2AD=2 cm,
∴AB= cm.
21.如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3
(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?
(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
【答案】(1)S1=S2+S3 (2)S1=S2+S3.说明略.
第 1 页 共 3 页
一、选择题:
1.下列各组数:①3、4、5 ②4、5、6 ③2.5、6、6.5 ④8、15、17,其中是勾股数的有( C )
A. 4组 B. 3组 C. 2组 D. 1组
2. 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为 ( C )
?
A. 米?????B. 米????C. (+1)米??????D. 3米???????
3、已知一个Rt△的两边长分别为3和4,则第三边长的平方是( D )
A.25?? ? ?? B.14??? ???? C.7??? ???? D.7或25
4.由下列条件不能判定△ABC为直角三角形的是( B )
A. ∠A+∠C=∠B B. a=,b=,c=
C. (b+a)(b-a)=c2 D. ∠A:∠B:∠C=5:3:2
5.如图1,一架梯子AB长为,斜靠在一面墙上,梯子底端B离墙,若梯子的顶端A下滑了(如图2),则梯子的底端在水平方向上滑动的距离为(A)
A. B.大于
C.介于和之间 D.介于和之间
6.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( D )
A. 90° B. 60° C. 30° D. 45°
7.一直角三角形的三边分别为2、3、x,那么x为( C )
A.??? ? B.? C.或???? D.无法确定
8.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( C )
(A) 米 (B) 米
(C)(+1)米 (D)3米
9.直角三角形的面积为S,斜边上的中线长为d,则这个三角形周长为( C )
A. B. C. D.
10. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( A )
①②③???B. ①②④???C. ①③④??????D. ①②③④???
二、填空题
11. 已知等腰三角形的一边长为10,面积为30,该三角形的周长为 .?
【答案】10+2或20+2或20+6
12.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为 ?? m.
【答案】2.2.
(2018云南)在△ABC中,AB=,AC=5.若BC边上的高等于3,则BC边的长为 .
【答案】1或9
14.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为________.
【答案】9
15.如图,在中,,,,现将沿进行翻折,使点刚好落在上,则__________.
【答案】
16.图甲是第七届国际数学教育大会(简称ICME~7)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,那么OA1,OA2,…,OA25这些线段中有 条线段的长度为正整数.?
【答案】5
解答题
17.如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
【答案】(1)∠BAD=135°;(2)四边形ABCD的面积 2+
解析:
(1)∵∠B=90°,AB=BC=2,
∴AC= =2 ,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
(2)连接AC,如图所示:
在直角△ABC中,AC为斜边,且AB=BC=2,则AC=,
∵AD=1,CD=3,
∴AC2+CD2=AC2,
即△ACD为直角三角形,且∠ADC=90°,
四边形ABCD的面积=S△ABC+S△ACD=AB×BC+AD×AC=2+.
如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.
?
【答案】如图,过点C作CG∥AB交ED的延长
?
?线于点G,连接FG.
?∵CG∥AB,∴∠B=∠DCG,∠BED=∠DGC.
?∵BD=CD,∴△BDE≌△CDG,(AAS)
?∴DE=DG,BE=CG.
?∵∠EDF=90°,∴DF垂直平分EG,
?∴EF=FG.
?∵∠A=90°,∴∠B+∠DCF=180°-90°=90°,
?∴∠DCF+∠DCG=∠FCG=90°.
?在Rt△CFG中,CG2+CF2=FG2,
?即BE2+CF2=EF2.
19.如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.(1)求证:CD=BE;????????????????????????????????????
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
(1)证明:∵在△ABC中,AC=BC,∠C=90°,∴△ABC是等腰直角三角形,∴∠B=45°,
∵DE⊥AB,∴△BDE是等腰直角三角形,∴DE=BE.
∵AD是△ABC的角平分线,∴CD=DE,∴CD=BE;
(2)解:∵由(1)知,△BDE是等腰直角三角形,DE=BE=CD,∴DE=BE=CD=2,
∴BD===2,∴AC=BC=CD+BD=2+2;
(3)证明:∵AD是△ABC的角平分线,DE⊥AB,∴CD=DE.
在Rt△ACD与Rt△AED中,∵,∴Rt△ACD≌Rt△AED,∴AE=AC.
∵由(1)知CD=BE,∴AB=AE+BE=AC+CD.
20.如图,在△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,垂足为A,CD=1 cm,求AB的长.
解:∵在△ABC中,∠BAC=120°,∠B=30°,
∴∠C=180°-120°-30°=30°,∠DAC=120°-90°=30°,
即∠DAC=∠C,
∴CD=AD=1 cm.
在Rt△ABD中,∠B=30°,BD=2AD=2 cm,
∴AB= cm.
21.如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3
(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?
(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
【答案】(1)S1=S2+S3 (2)S1=S2+S3.说明略.
第 1 页 共 3 页
