高中数学第二章圆锥曲线与方程2.4.1抛物线的标准方程课件 新人教B版选修2_1
文档属性
| 名称 | 高中数学第二章圆锥曲线与方程2.4.1抛物线的标准方程课件 新人教B版选修2_1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-10 11:29:59 | ||
图片预览






文档简介
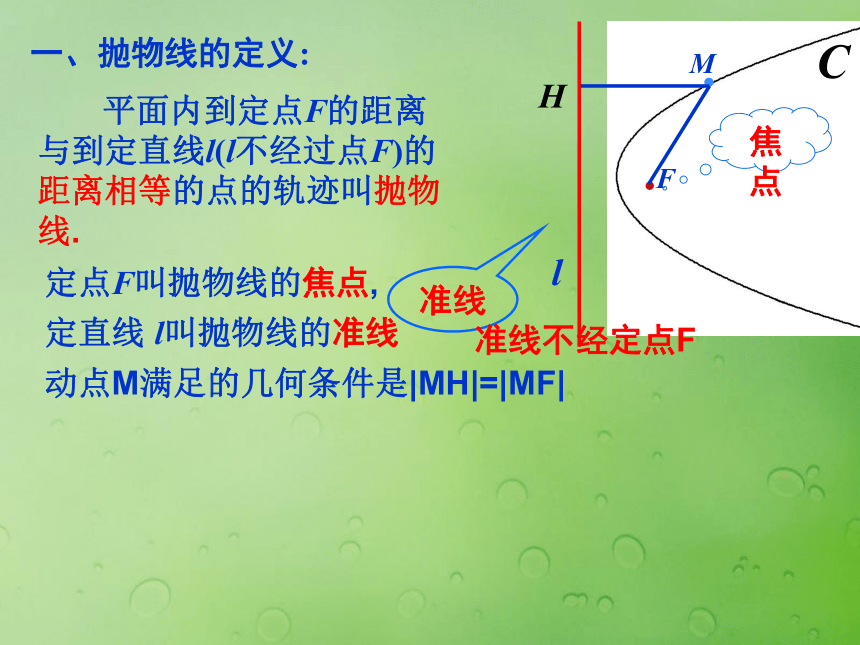
课件19张PPT。观音桥音乐喷泉数学的魅力来源于生活,又应用于生活菜园坝长江大桥数学是一门别具匠心的艺术2.4.1抛物线及其标准方程M·Fl· 平面内到定点F的距离与到定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.定点F叫抛物线的焦点,准线焦点一、抛物线的定义:定直线 l叫抛物线的准线动点M满足的几何条件是|MH|=|MF|准线不经定点F二、方程的建立 1.建系-- 建立适当的直角坐标系,用有序实数对(x,y)表示曲线上任一点M的坐标;2.写条件-- 根据已知条件写出点M满足的几何条件。3.列方程--用M坐标表示条件,列出方程f(x,y)=0;4.化简--化方程f(x,y)=0为最简形式;5.证明--证明以化简后的方程的解为坐标的点都是曲线上的点。(不要求证明,但要检验是.否产生增解或漏解.)求曲线方程的一般步骤?三、标准方程 把方程 y2 = 2px (p>0)叫做焦点在 x 轴正半轴上的抛物线的标准方程. 且 p的几何意义是:焦点到准线的距离lM(x,y)焦点坐标是准线方程为:y2=-2px
(p>0)四种抛物线的对比y2=2px(p>0)x2=2py(p>0)x2=-2py
(p>0)···(1)方程都是关于x,y的二元二次方程;(2)左边是二次项;(3)右边是另一个变量的一次项;(4)方程中只有一个参数p(焦点到准线的距离)(5)一次项确定对称轴,系数的正负确定开口放向;(6)若x是一次项,系数是焦点横坐标的4倍;(7)若y是一次项,系数是焦点纵坐标的4倍。四:课堂游戏游戏规则:(1)全班分成9个小组,第一小组派一名代表说出2个抛物线方程,随机喊下一小组一名同学说出其对称轴和开口方向,焦点坐标和准线方程.
(2)从第四小组开始改成说出2个不同的焦点坐标,随机喊下一小组 一名同学说出抛物线的方程。
(3)从第七小组开始改成说出准线方程,随机喊下一小组一名同学说出抛物线方程。
例1 已知抛物线的标准方程是 y 2 = 6 x ,求它的焦点坐标及准线方程。四:典型例题解:因为抛物线的方程为y 2 = 6 x ,所以焦点坐标为 ,准线方程为 。因为2p=6,p=3 A.(0,1) B.(1,0) C. (0, ) D.( ,0 )(2)抛物线 y 2 = a x (a≠0) ,指出它的焦点坐标及准线方程。变式训练1(1)抛物线 y = x2 的焦点坐标是( )解:抛物线的方程为y 2 = a x (a≠0) ,
(1)当a>0时,抛物线的图象是
因为2p=a,所以p= 。
所以焦点坐标为 ,准线方程为x=综上所述,焦点坐标为 ,准线方程为x=
(2)当a<0时,抛物线的图象是
因为-2p=-a,所以p= 。
所以焦点坐标为 ,准线方程为x=小结.(1)化标准:把所给的方程化成标准形式;(2)明方向:画出图象,明确抛物线的开口方向;(3)求p值:由方程求得p的值;(4)写性质:写出焦点坐标和准线方程。已知抛物线的方程如何求焦点坐标和准线方程例2 (1)已知抛物线的焦点坐标是 F(0,-2),求抛物线的标准方程. (2)焦点到准线的距离是2,求抛物线的标准方程解:由题意得,抛物线的图象如右图所以 ,p=4,所以方程为x2=-8y.解:抛物线的方程为:x2=4y,x2=-4y,y2=4x,y2=-4x设抛物线的方程为x2=-2py(2)求过点A(3,2)的抛物线的标准方程(1)抛物线的准线方程为 x = 1 ,则抛物线的标准方程是 ( )变式训练2 A.y2=-4x B. y2=4x C. x2=4y D.x2=-4y解:因为方程过A(3,2)所以抛物线的图象可能有以下两种情况第一种第二种(1)若图象是第一种情况,设抛物线的方程为y2=2px,将A(3,2)代入,得到p= ,所以抛物线的方程为y2= x。(2)若图象是第二种情况,设抛物线的方程为x2=2py,将A(3,2)代入,得到p= ,所以抛物线的方程为x2= y。小结:用待定系数法求抛物线标准方程的步骤(1)画图象:根据题意画出抛物线的图象;(2)设方程:设出抛物线的标准方程;(3)解方程:解关于参数p的方程,求出p的值;(4)得方程:根据参数p的值,写出所求的标准方程;4.四种抛物线方程的特点。1.抛物线的定义:2.抛物线的标准方程有四种不同的形式:3.p的几何意义是:焦 点 到 准 线 的 距 离五 课堂小结:每一对焦点和准线对应一种形式.5、圆锥曲线最重要的思想就是数形结合的思想,在抛物线这一节中表现的更加淋漓尽致。数学虽然没有华丽的外表,
但是它是一门简捷美丽的学科P66思考: 二次函数 的图象为什么是抛物线? 必做作业:P67 1,2,3六 课后作业
(p>0)四种抛物线的对比y2=2px(p>0)x2=2py(p>0)x2=-2py
(p>0)···(1)方程都是关于x,y的二元二次方程;(2)左边是二次项;(3)右边是另一个变量的一次项;(4)方程中只有一个参数p(焦点到准线的距离)(5)一次项确定对称轴,系数的正负确定开口放向;(6)若x是一次项,系数是焦点横坐标的4倍;(7)若y是一次项,系数是焦点纵坐标的4倍。四:课堂游戏游戏规则:(1)全班分成9个小组,第一小组派一名代表说出2个抛物线方程,随机喊下一小组一名同学说出其对称轴和开口方向,焦点坐标和准线方程.
(2)从第四小组开始改成说出2个不同的焦点坐标,随机喊下一小组 一名同学说出抛物线的方程。
(3)从第七小组开始改成说出准线方程,随机喊下一小组一名同学说出抛物线方程。
例1 已知抛物线的标准方程是 y 2 = 6 x ,求它的焦点坐标及准线方程。四:典型例题解:因为抛物线的方程为y 2 = 6 x ,所以焦点坐标为 ,准线方程为 。因为2p=6,p=3 A.(0,1) B.(1,0) C. (0, ) D.( ,0 )(2)抛物线 y 2 = a x (a≠0) ,指出它的焦点坐标及准线方程。变式训练1(1)抛物线 y = x2 的焦点坐标是( )解:抛物线的方程为y 2 = a x (a≠0) ,
(1)当a>0时,抛物线的图象是
因为2p=a,所以p= 。
所以焦点坐标为 ,准线方程为x=综上所述,焦点坐标为 ,准线方程为x=
(2)当a<0时,抛物线的图象是
因为-2p=-a,所以p= 。
所以焦点坐标为 ,准线方程为x=小结.(1)化标准:把所给的方程化成标准形式;(2)明方向:画出图象,明确抛物线的开口方向;(3)求p值:由方程求得p的值;(4)写性质:写出焦点坐标和准线方程。已知抛物线的方程如何求焦点坐标和准线方程例2 (1)已知抛物线的焦点坐标是 F(0,-2),求抛物线的标准方程. (2)焦点到准线的距离是2,求抛物线的标准方程解:由题意得,抛物线的图象如右图所以 ,p=4,所以方程为x2=-8y.解:抛物线的方程为:x2=4y,x2=-4y,y2=4x,y2=-4x设抛物线的方程为x2=-2py(2)求过点A(3,2)的抛物线的标准方程(1)抛物线的准线方程为 x = 1 ,则抛物线的标准方程是 ( )变式训练2 A.y2=-4x B. y2=4x C. x2=4y D.x2=-4y解:因为方程过A(3,2)所以抛物线的图象可能有以下两种情况第一种第二种(1)若图象是第一种情况,设抛物线的方程为y2=2px,将A(3,2)代入,得到p= ,所以抛物线的方程为y2= x。(2)若图象是第二种情况,设抛物线的方程为x2=2py,将A(3,2)代入,得到p= ,所以抛物线的方程为x2= y。小结:用待定系数法求抛物线标准方程的步骤(1)画图象:根据题意画出抛物线的图象;(2)设方程:设出抛物线的标准方程;(3)解方程:解关于参数p的方程,求出p的值;(4)得方程:根据参数p的值,写出所求的标准方程;4.四种抛物线方程的特点。1.抛物线的定义:2.抛物线的标准方程有四种不同的形式:3.p的几何意义是:焦 点 到 准 线 的 距 离五 课堂小结:每一对焦点和准线对应一种形式.5、圆锥曲线最重要的思想就是数形结合的思想,在抛物线这一节中表现的更加淋漓尽致。数学虽然没有华丽的外表,
但是它是一门简捷美丽的学科P66思考: 二次函数 的图象为什么是抛物线? 必做作业:P67 1,2,3六 课后作业
