八年级下册第17章一元二次方程复习试卷(前三节)
文档属性
| 名称 | 八年级下册第17章一元二次方程复习试卷(前三节) |  | |
| 格式 | zip | ||
| 文件大小 | 82.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 07:33:47 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
一元二次方程复习
一、单选题(共15题;共45分)
1. ( 3分 ) 关于x的方程(m+1)x2+2mx-3=0是一元二次方程,则m的取值是(??????? )
A.任意实数 B.m≠1 C.m≠-1 D.m>1
2. ( 3分 ) 一元二次方程 化成一般式后,二次项系数为1,一次项系数为 ,则 的值为(?? ).
A.???????????????????????????B.?1??????????????????????????????C.????????????????????????????????D.?
3. ( 3分 ) 一个三角形的两边长分别为3和6,第三边的边长是方程x2-6x+8=0的根,则这个三角形的周长是(??????? )
A.11 B.11或13 C.13 D.以上选项都不正确
4. ( 3分 ) 三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是(?? )
A.?24??????????????????B.?48????????????????????C.?24或8 ??????????????????????D.?8
5. ( 3分 ) 用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为(?? )
A.?(x+ )2= ???????????????????????????????????????B.?(x+ )2=
C.?(x﹣ )2= ??????????????????????????????????????D.?(x﹣ )2=
6. ( 3分 ) 若x=1是方程 的一个根,则方程的另一个根与k的值是(?? )
A.?? 2,3??????????????????????B.?-2,3???????????????????????????????????C.?-2,-3???????????????????????????????????D.?2,-3
7. ( 3分 ) 用配方法解方程x2﹣2x=3时,原方程应变形为(?? )
A.?(x+1)2=2?????????????B.?(x﹣1)2=2?????????????C.?(x+1)2=4????????????D.?(x﹣1)2=4
8. ( 3分 ) 对二次三项式 变形正确的是(?? )
A.??????? ?B.?????????????????C.??????????? D.?
9. ( 3分 ) 用公式法解方程x2﹣4x﹣2=0,其中b2﹣4ac的值是(?? )
A.?16?????????????????????????????B.?24???????????????????????????????????C.?8????????????????????????????????D.?4
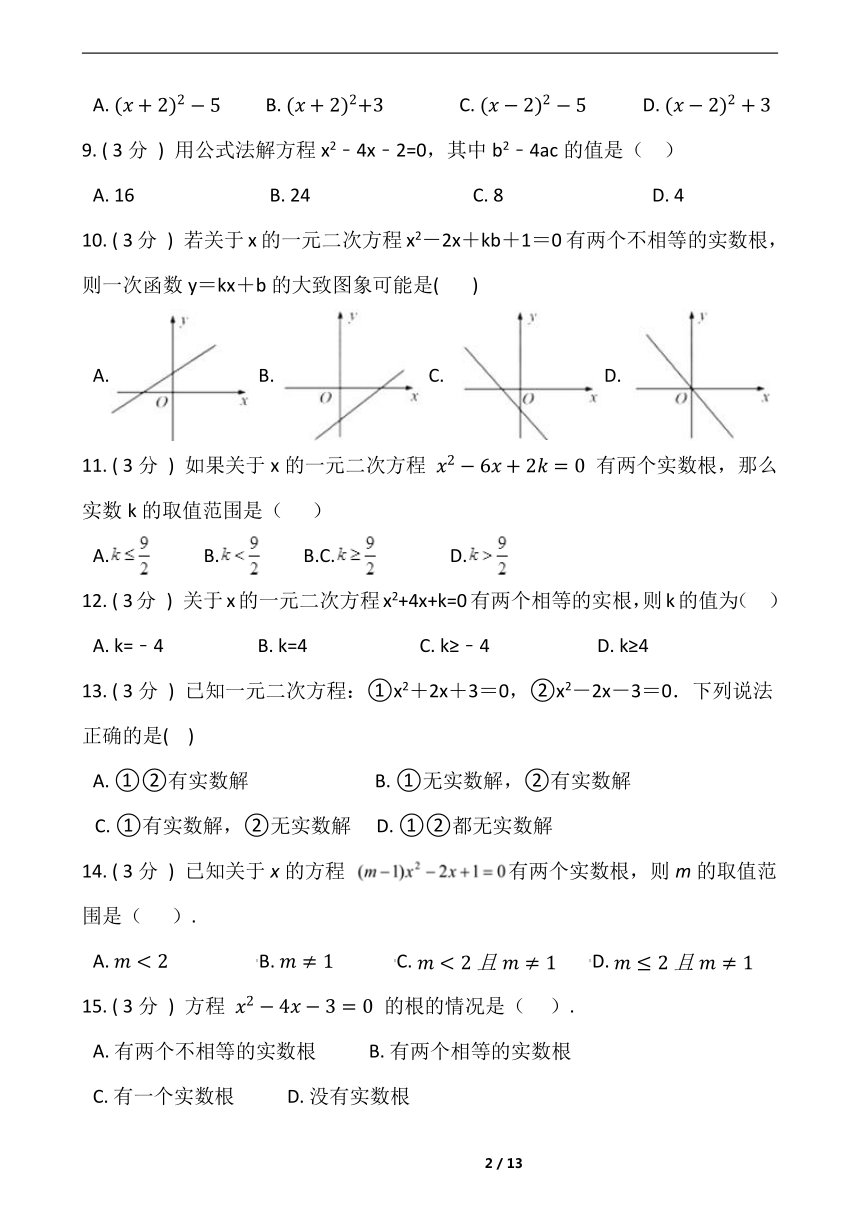
10. ( 3分 ) 若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是(? ????)
A.B.C.D.
11. ( 3分 ) 如果关于x的一元二次方程 有两个实数根,那么实数k的取值范围是(???? )
A. B. B.C. D.
12. ( 3分 ) 关于x的一元二次方程x2+4x+k=0有两个相等的实根,则k的值为(?? )
A.?k=﹣4????????????????????B.?k=4????????????????????????C.?k≥﹣4???????????????????????D.?k≥4
13. ( 3分 ) 已知一元二次方程:①x2+2x+3=0,②x2-2x-3=0.下列说法正确的是(?? )
A.?①②有实数解????? B.?①无实数解,②有实数解?????
C.?①有实数解,②无实数解?????D.?①②都无实数解
14. ( 3分 ) 已知关于x的方程 有两个实数根,则m的取值范围是(???? ).
A.????????????????????B.??????????????C.????????D.?
15. ( 3分 ) 方程 的根的情况是(??? ).
A.?有两个不相等的实数根???????????B.?有两个相等的实数根???????????
C.?有一个实数根???????????D.?没有实数根
二、填空题(共6题;共24分)
16. ( 4分 ) 若(m﹣2) ﹣mx+1=0是一元二次方程,则m的值为________.
17. ( 4分 ) 当m=________时,关于x的方程 是一元二次方程;
18. ( 4分 ) 一元二次方程x2-6x-5=0通过配方可变形为________
19. ( 4分 ) 一个等腰三角形的两边长分别是方程(x﹣2)(x﹣5)=0的两根,则该等腰三角形的周长是________.
20. ( 4分 ) 已知关于x的方程x2+(2k+1)x+k2=0的两个实数根的平方和是11,则k=________.
( 4分 ) 若关于 的一元二次方程 有实数根,则 的取值范围是________.
计算题
22. ( 15分 ) 解方程:
(1)
(2)
(3)
( 4 ) 2x2-4x+5=0
四、解答题(共8题;共74分)
23. ( 8分 ) 若 是关于x的一元二次方程,则a是多少 ,且该一元二次方程的解为多少?
24. ( 8分 ) 已知菱形的边长是5cm,一条对角线的一半长是方程x2﹣3x﹣4=0的根,你能求出这个菱形的面积吗?
25. ( 8分 ) 解关于x的方程x2-2mx+m2-2=0.
26. ( 10分 ) 已知关于x的一元二次方程x2-(m+2)x+(2m-1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根。并求以此两根为边长的直角三角形的周长。
27. ( 15分 ) 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
答案解析部分
一、单选题
1.【答案】 C
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:∵方程(m+1)x2+2mx-3=0是一元二次方程,
∴ m+1≠0
解之:m≠-1,
故答案为:C
【分析】利用一元二次方程的定义,二次项系数不等于0,建立关于m的不等式,求解即可。
2.【答案】 B
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:化成一般形式x2?-ax+1=0,
∵一次项系数为-1,
∴--a=-1,
则a=1.
故答案为:B
【分析】先把方程化成一般形式x2-ax+1=0,再由一次项系数为-1,可求出a的值.
3.【答案】 C
【考点】因式分解法解一元二次方程,三角形三边关系
【解析】【解答】∵方程 的两根为:
∵三角形的两边长分别为3和6,第三边不能取2,只能取4,则这个三角形的周长为:13,
故答案为:C
【分析】利用因式分解法求出方程的两个根,再根据三角形三边关系定理确定出第三边的长,然后求出这个三角形的周长。
4.【答案】 C
【考点】配方法解一元二次方程
【解析】【解答】解: 首先解方程x2-16x+60=0得,
原方程可化为:(x-8)2=4,
解得x1=6或x2=10;
如图(1)根据勾股定理的逆定理,△ABC为直角三角形,
S△ABC= ×6×8=24;
如图(2)AD= =
S△ABC= ×8× = .
故答案为:C
【分析】先解方程求得x的值,这两个值与三角形的另外两边都可以组成三角形,一个为等腰三角形,一根为直角三角形,分别求其面积即可.
5.【答案】 A
【考点】配方法解一元二次方程
【解析】【解答】解:ax2+bx+c=0,
ax2+bx=﹣c,
x2+ x=﹣ ,
x2+ x+( )2=﹣ +( )2 ,
(x+ )2= ,故答案为:A
【分析】先将二次项系数化为1,再结合一次项与完全平方公式进行配方.
6.【答案】 D
【考点】一元二次方程的根,因式分解法解一元二次方程
【解析】【解答】将x=1代入方程,得
k+1+2=0,k=-3,故原方程为
因式分解法
【分析】使一元二次方程两边相等的未知数的值,叫做一元二次方程的解,根据定义将x=1代入方程,得k+1+2=0,k=-3,故原方程为 - 3 x +2 = 0,解方程得=2,=1.
7.【答案】D
【考点】配方法解一元二次方程
【解析】【解答】解:x2﹣2x=3,
x2﹣2x+1=3+1,
(x﹣1)2=4,
故选D.
【分析】配方,即可得出选项.
8.【答案】 C
【考点】配方法的应用
【解析】【解答】解:x2-4x-1= x2-4x +22-22-1=(x-2)2-5.
故答案为:C
【分析】配方法的理论依据是公式a2±2ab+b2=(a±b)2.根据配方法“先将一元二次方程的二次项系数化为1,然后在方程两边同时加上一次项系数一半的平方”即可求解.
9.【答案】B
【考点】解一元二次方程-公式法
【解析】【解答】解:∵a=1,b=﹣4,c=﹣2, ∴b2﹣4ac=(﹣4)2﹣4×1×(﹣2)=16+8=24,
故选:B.
【分析】将a、b、c的值代入b2﹣4ac即可得.
10.【答案】 B
【考点】一元二次方程根的判别式及应用,一次函数图像、性质与系数的关系
【解析】【解答】∵一元二次方程x2-2x+kb+1=0有两个不相等的实数根,
∴b2-4ac>0
∴4-4(kb+1)>0
解之:kb<0
当k>0,b<0时,直线 y=kx+b 经过第一、三、四象限
故答案为;B
【分析】由一元二次方程x2-2x+kb+1=0有两个不相等的实数根,可得出b2-4ac>0,求出kb<0,再分情况讨论,就可得出答案。
11.【答案】 A
【考点】一元二次方程根的判别式及应用
【解析】【解答】解:∵一元二次方程 有两个实数根,
∴ ,∴ ,
故答案为:A
【分析】根据一元二次方程根的判别式,得出b2-4ac≥0,建立关于k的不等式,即可得出k的取值范围。
12.【答案】 B
【考点】一元二次方程根的判别式及应用
【解析】【解答】解:∵一元二次方程x2+4x+k=0有两个相等的实根,
∴△=42﹣4k=0,
解得:k=4,
故答案为:B
【分析】一元二次方程的判别式,判别式?>0,方程有两个不相等的实数根;?=0,方程有两个相等的实数根;?<0,方程没有实数根.
13.【答案】 B
【考点】一元二次方程根的判别式及应用
【解析】【解答】方程①的判别式△=4-12=-8,则①没有实数解;②的判别式△=4+12=16,则②有实数解.故答案为:B.
【分析】一元二次方程的根的判别式-4ac0时,方程有两个不相等的实数根;,-4ac=0时,方程有两个相等的实数根;-4ac0时,方程没有实数根。根据题意计算出方程①的判别式△=4-12=-80,则①没有实数解;②的判别式△=4+12=16,则②有实数解.
14.【答案】D
【考点】根的判别式
【解析】【解答】解:∵关于x的方程(m-1)x2-2x+1=0有两个不相等的实数根,
∴m-1≠0,且△>0,即4-4(m-1)>0,解得m<2,
∴m的取值范围是 m<2且m≠1.
故选D.
【分析】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.
15.【答案】A
【考点】根的判别式
【解析】【解答】解:要判断方程x2-4x-3=0的根的情况就要求出方程的根的判别式,然后根据判别式的正负情况即可作出判断.
解:∵a=1,b=-4,c=3,∴△=16-12=4,∴有两个不相等的实数根.故选A.
【分析】一元二次方程根的情况与判别式△的关系:(1)△>0,方程有两个不相等的实数根;(2)△=0,方程有两个相等的实数根;(3)△<0,方程没有实数根.
二、填空题
16.【答案】﹣2
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:根据题意得: ,
解得:m=﹣2.
故答案是:﹣2.
【分析】一元二次方程的定义是含有一个未知数,且未知数的次数是2的方程(a≠0);得到m2-2=2且m-2≠0,求出m的值.
17.【答案】-3
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:由一元二次方程的特点得m2-7=2,即m=±3,m=3舍去,即m=-3时,原方程是一元二次方程.
故答案为:-3.【分析】根据一元二次方程的定义可得m2-7=2,且m-3≠0,从而求出符合条件的m值.
18.【答案】
【考点】配方法解一元二次方程
【解析】【解答】解:一元二次方程x2-6x-5=0通过配方可变形为
故答案为:
【分析】先将常数项移到方程的右边,再在方程两边同时加上一次项系数一半的平方,即可得出答案。
19.【答案】12
【考点】因式分解法解一元二次方程,三角形三边关系
【解析】【解答】解:由方程(x﹣2)(x﹣5)=0可得x﹣2=0或x﹣5=0,
解得:x=2或x=5,
当三角形的三边为2、2、5时,2+2<5,不能构成三角形,舍去;
当三角形的三边为2、5、5时,2+5>5,可以构成三角形,其周长为2+5+5=12,
故答案为:12.
【分析】根据因式分解法求出方程的解,根据等腰三角形的性质和根据两边之和大于第三边,两边之差小于第三边,求出等腰三角形的周长.
20.【答案】 ﹣1+
【考点】一元二次方程根的判别式及应用,一元二次方程的根与系数的关系
【解析】【解答】解:设方程x2+(2k+1)x+k2=0的两个实数根分别为m、n,
则有:m+n=﹣2k﹣1,mn=k2 ,
∵m2+n2=(m+n)2﹣2mn=11,
∴(﹣2k﹣1)2﹣2k2=11,即k2+2k﹣5=0,
解得:k=﹣1﹣ 或k=﹣1+ .
∵方程有实数根,
∴△=(2k+1)2﹣4k2=4k+1≥0,
∴k≥﹣ ,
∴k=﹣1+ .
故答案为:﹣1+ .
【分析】设方程x2+(2k+1)x+k2=0的两个实数根分别为m、n,根据根与系数的关系可得出m+n=﹣2k﹣1、mn=k2 , 结合m2+n2=11即可得出关于k的一元二次方程,解方程可得出k的值,再根据方程有解结合根的判别式即可得出关于k的一元一次不等式,解不等式可得出k的取值范围,由此即可确定k的值.
21.【答案】
【考点】根的判别式
【解析】【解答】由题意得 ?,解得 .
故答案为:0 ≤ m ≤ 4 3 且 m ≠ 1 ?.
【分析】本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解答此题的关键.
27.【答案】 (1)解:原方程可化为: ,两边开平方得: ,
∴
(2)解:因式分解得: ,∴
(3)解:∵ ,
∴
【考点】直接开平方法解一元二次方程,配方法解一元二次方程,因式分解法解一元二次方程
【解析】【分析】(1)利用直接开平方法求出方程的解即可。
(2)观察方程的特点:右边为0,左边可以分解因式,因此利用因式分解法解方程。
(3)利用公式法解方程即可。
三、计算题
22.【答案】解:2x2-4x+5=0,
∵a=2,b=-4,c=5,∴b2-4ac=(-4)2-4×2×5=-24<0,
∴该方程没有实数根
【考点】根的判别式
【解析】【分析】由题意有a=2,b=-4,c=5,所以b2-4ac=(-4)2-4×2×5=-24<0,根据一元二次方程的根与系数的关系可得方程没有实数根。
23.【答案】解:移项得:
原方程无解
【考点】一元二次方程根的判别式及应用
【解析】【分析】先将方程化为一般形式,?x2? 3x?8=0,所以a=1,b=?3,c=8,
b2?4ac=9?4×1×8=?23<0,根据一元二次方程的根的判别式可知原方程无实数根。
三、解答题
24.【答案】解:|2a+3|=2
2a+3=±2
当 时,
当 时
【考点】一元二次方程的定义,解一元二次方程-公式法
【解析】【分析】根据一元二次方程的定义可得|2a+3|=2,且a+1不为0,解得 , 再将a = - 或 a = - 代入原方程即可求解。
25.【答案】解:∵x2﹣3x﹣4=0,
∴x=4或x=﹣1(舍),
∵菱形的边长是5cm,
∴菱形的另外一条对角线=2 ?=6cm,
∴菱形的面积为= ×6×8=24cm2
【考点】因式分解法解一元二次方程,菱形的性质
【解析】【分析】先解一元二次方程,那么一元二次方程的正跟即为菱形另一条对角线的一半长,那么菱形的面积即为两条对角线长度积的一半.
26.【答案】 解:∵a=1,b=-2m,c=m2-2,
∴ ,
∴ ,
【考点】公式法解一元二次方程
【解析】【分析】由题意有,a=1,b=-2m,c=m2-2,所以根据一元二次方程的求根公式x=求解即可。
25.【答案】(1)解:由判别式可得(m+2)2-4(2m-1)=m2+4m+4-8m+4= m2-4m+8=(m-2)2+4>0.
所以方程恒有两个不相等的实数根。
(2)解:把x=1代入方程可得1-(m+2)+(2m-1)=0,解得m=2,
把m=2代入方程可整理得x2-4x+3=0,解得x1=1,x2=3.
当1和3都是直角边的边长时,斜边长为 ,周长为4+ 。
当3是斜边长时,另一条边长是 ,周长为4+ 。
【考点】根的判别式
【解析】【分析】(1)方程的解与根的判别式有关,求出判别式的范围,再判断根的情况;(2)由于方程中有个未知数m,可以将x=1代入方程先求出m的解;再将m的值代入,解出一元二次方程的两个解,则分类讨论两个解分别是直角边还是斜边,求出第三条边,写出周长。
27.【答案】(1)解:△ABC是等腰三角形.理由如下:
将x=-1代入方程得a+c-2b+a-c=0,
即a=b,
则△ABC是等腰三角形.
(2)解:△ABC是直角三角形.理由如下:
判别式=(2b)2-4(a+c)(a-c)=4b2-4a2+4c2=4(b2-a2-c2)=0,
即b2=a2+c2.
则△ABC是直角三角形
(3)解:∵△ABC是等边三角形,
∴a=b=c,
∴方程可化为2ax2+2ax+=0,
∴2ax(x+1)=0,
∴x1=0,x2=-1.
【考点】根的判别式,一元二次方程的应用
【解析】【分析】(1)将x=-1的值代入,整理方程可得a,b,c的数量关系;
(2)根据判别式=b2-4ac=0,整理可得a,b,c的数量关系;
(3)根据a=b=c代入方程可解得方程的解.
1 / 1
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
一元二次方程复习
一、单选题(共15题;共45分)
1. ( 3分 ) 关于x的方程(m+1)x2+2mx-3=0是一元二次方程,则m的取值是(??????? )
A.任意实数 B.m≠1 C.m≠-1 D.m>1
2. ( 3分 ) 一元二次方程 化成一般式后,二次项系数为1,一次项系数为 ,则 的值为(?? ).
A.???????????????????????????B.?1??????????????????????????????C.????????????????????????????????D.?
3. ( 3分 ) 一个三角形的两边长分别为3和6,第三边的边长是方程x2-6x+8=0的根,则这个三角形的周长是(??????? )
A.11 B.11或13 C.13 D.以上选项都不正确
4. ( 3分 ) 三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是(?? )
A.?24??????????????????B.?48????????????????????C.?24或8 ??????????????????????D.?8
5. ( 3分 ) 用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为(?? )
A.?(x+ )2= ???????????????????????????????????????B.?(x+ )2=
C.?(x﹣ )2= ??????????????????????????????????????D.?(x﹣ )2=
6. ( 3分 ) 若x=1是方程 的一个根,则方程的另一个根与k的值是(?? )
A.?? 2,3??????????????????????B.?-2,3???????????????????????????????????C.?-2,-3???????????????????????????????????D.?2,-3
7. ( 3分 ) 用配方法解方程x2﹣2x=3时,原方程应变形为(?? )
A.?(x+1)2=2?????????????B.?(x﹣1)2=2?????????????C.?(x+1)2=4????????????D.?(x﹣1)2=4
8. ( 3分 ) 对二次三项式 变形正确的是(?? )
A.??????? ?B.?????????????????C.??????????? D.?
9. ( 3分 ) 用公式法解方程x2﹣4x﹣2=0,其中b2﹣4ac的值是(?? )
A.?16?????????????????????????????B.?24???????????????????????????????????C.?8????????????????????????????????D.?4
10. ( 3分 ) 若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是(? ????)
A.B.C.D.
11. ( 3分 ) 如果关于x的一元二次方程 有两个实数根,那么实数k的取值范围是(???? )
A. B. B.C. D.
12. ( 3分 ) 关于x的一元二次方程x2+4x+k=0有两个相等的实根,则k的值为(?? )
A.?k=﹣4????????????????????B.?k=4????????????????????????C.?k≥﹣4???????????????????????D.?k≥4
13. ( 3分 ) 已知一元二次方程:①x2+2x+3=0,②x2-2x-3=0.下列说法正确的是(?? )
A.?①②有实数解????? B.?①无实数解,②有实数解?????
C.?①有实数解,②无实数解?????D.?①②都无实数解
14. ( 3分 ) 已知关于x的方程 有两个实数根,则m的取值范围是(???? ).
A.????????????????????B.??????????????C.????????D.?
15. ( 3分 ) 方程 的根的情况是(??? ).
A.?有两个不相等的实数根???????????B.?有两个相等的实数根???????????
C.?有一个实数根???????????D.?没有实数根
二、填空题(共6题;共24分)
16. ( 4分 ) 若(m﹣2) ﹣mx+1=0是一元二次方程,则m的值为________.
17. ( 4分 ) 当m=________时,关于x的方程 是一元二次方程;
18. ( 4分 ) 一元二次方程x2-6x-5=0通过配方可变形为________
19. ( 4分 ) 一个等腰三角形的两边长分别是方程(x﹣2)(x﹣5)=0的两根,则该等腰三角形的周长是________.
20. ( 4分 ) 已知关于x的方程x2+(2k+1)x+k2=0的两个实数根的平方和是11,则k=________.
( 4分 ) 若关于 的一元二次方程 有实数根,则 的取值范围是________.
计算题
22. ( 15分 ) 解方程:
(1)
(2)
(3)
( 4 ) 2x2-4x+5=0
四、解答题(共8题;共74分)
23. ( 8分 ) 若 是关于x的一元二次方程,则a是多少 ,且该一元二次方程的解为多少?
24. ( 8分 ) 已知菱形的边长是5cm,一条对角线的一半长是方程x2﹣3x﹣4=0的根,你能求出这个菱形的面积吗?
25. ( 8分 ) 解关于x的方程x2-2mx+m2-2=0.
26. ( 10分 ) 已知关于x的一元二次方程x2-(m+2)x+(2m-1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根。并求以此两根为边长的直角三角形的周长。
27. ( 15分 ) 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
答案解析部分
一、单选题
1.【答案】 C
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:∵方程(m+1)x2+2mx-3=0是一元二次方程,
∴ m+1≠0
解之:m≠-1,
故答案为:C
【分析】利用一元二次方程的定义,二次项系数不等于0,建立关于m的不等式,求解即可。
2.【答案】 B
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:化成一般形式x2?-ax+1=0,
∵一次项系数为-1,
∴--a=-1,
则a=1.
故答案为:B
【分析】先把方程化成一般形式x2-ax+1=0,再由一次项系数为-1,可求出a的值.
3.【答案】 C
【考点】因式分解法解一元二次方程,三角形三边关系
【解析】【解答】∵方程 的两根为:
∵三角形的两边长分别为3和6,第三边不能取2,只能取4,则这个三角形的周长为:13,
故答案为:C
【分析】利用因式分解法求出方程的两个根,再根据三角形三边关系定理确定出第三边的长,然后求出这个三角形的周长。
4.【答案】 C
【考点】配方法解一元二次方程
【解析】【解答】解: 首先解方程x2-16x+60=0得,
原方程可化为:(x-8)2=4,
解得x1=6或x2=10;
如图(1)根据勾股定理的逆定理,△ABC为直角三角形,
S△ABC= ×6×8=24;
如图(2)AD= =
S△ABC= ×8× = .
故答案为:C
【分析】先解方程求得x的值,这两个值与三角形的另外两边都可以组成三角形,一个为等腰三角形,一根为直角三角形,分别求其面积即可.
5.【答案】 A
【考点】配方法解一元二次方程
【解析】【解答】解:ax2+bx+c=0,
ax2+bx=﹣c,
x2+ x=﹣ ,
x2+ x+( )2=﹣ +( )2 ,
(x+ )2= ,故答案为:A
【分析】先将二次项系数化为1,再结合一次项与完全平方公式进行配方.
6.【答案】 D
【考点】一元二次方程的根,因式分解法解一元二次方程
【解析】【解答】将x=1代入方程,得
k+1+2=0,k=-3,故原方程为
因式分解法
【分析】使一元二次方程两边相等的未知数的值,叫做一元二次方程的解,根据定义将x=1代入方程,得k+1+2=0,k=-3,故原方程为 - 3 x +2 = 0,解方程得=2,=1.
7.【答案】D
【考点】配方法解一元二次方程
【解析】【解答】解:x2﹣2x=3,
x2﹣2x+1=3+1,
(x﹣1)2=4,
故选D.
【分析】配方,即可得出选项.
8.【答案】 C
【考点】配方法的应用
【解析】【解答】解:x2-4x-1= x2-4x +22-22-1=(x-2)2-5.
故答案为:C
【分析】配方法的理论依据是公式a2±2ab+b2=(a±b)2.根据配方法“先将一元二次方程的二次项系数化为1,然后在方程两边同时加上一次项系数一半的平方”即可求解.
9.【答案】B
【考点】解一元二次方程-公式法
【解析】【解答】解:∵a=1,b=﹣4,c=﹣2, ∴b2﹣4ac=(﹣4)2﹣4×1×(﹣2)=16+8=24,
故选:B.
【分析】将a、b、c的值代入b2﹣4ac即可得.
10.【答案】 B
【考点】一元二次方程根的判别式及应用,一次函数图像、性质与系数的关系
【解析】【解答】∵一元二次方程x2-2x+kb+1=0有两个不相等的实数根,
∴b2-4ac>0
∴4-4(kb+1)>0
解之:kb<0
当k>0,b<0时,直线 y=kx+b 经过第一、三、四象限
故答案为;B
【分析】由一元二次方程x2-2x+kb+1=0有两个不相等的实数根,可得出b2-4ac>0,求出kb<0,再分情况讨论,就可得出答案。
11.【答案】 A
【考点】一元二次方程根的判别式及应用
【解析】【解答】解:∵一元二次方程 有两个实数根,
∴ ,∴ ,
故答案为:A
【分析】根据一元二次方程根的判别式,得出b2-4ac≥0,建立关于k的不等式,即可得出k的取值范围。
12.【答案】 B
【考点】一元二次方程根的判别式及应用
【解析】【解答】解:∵一元二次方程x2+4x+k=0有两个相等的实根,
∴△=42﹣4k=0,
解得:k=4,
故答案为:B
【分析】一元二次方程的判别式,判别式?>0,方程有两个不相等的实数根;?=0,方程有两个相等的实数根;?<0,方程没有实数根.
13.【答案】 B
【考点】一元二次方程根的判别式及应用
【解析】【解答】方程①的判别式△=4-12=-8,则①没有实数解;②的判别式△=4+12=16,则②有实数解.故答案为:B.
【分析】一元二次方程的根的判别式-4ac0时,方程有两个不相等的实数根;,-4ac=0时,方程有两个相等的实数根;-4ac0时,方程没有实数根。根据题意计算出方程①的判别式△=4-12=-80,则①没有实数解;②的判别式△=4+12=16,则②有实数解.
14.【答案】D
【考点】根的判别式
【解析】【解答】解:∵关于x的方程(m-1)x2-2x+1=0有两个不相等的实数根,
∴m-1≠0,且△>0,即4-4(m-1)>0,解得m<2,
∴m的取值范围是 m<2且m≠1.
故选D.
【分析】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.
15.【答案】A
【考点】根的判别式
【解析】【解答】解:要判断方程x2-4x-3=0的根的情况就要求出方程的根的判别式,然后根据判别式的正负情况即可作出判断.
解:∵a=1,b=-4,c=3,∴△=16-12=4,∴有两个不相等的实数根.故选A.
【分析】一元二次方程根的情况与判别式△的关系:(1)△>0,方程有两个不相等的实数根;(2)△=0,方程有两个相等的实数根;(3)△<0,方程没有实数根.
二、填空题
16.【答案】﹣2
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:根据题意得: ,
解得:m=﹣2.
故答案是:﹣2.
【分析】一元二次方程的定义是含有一个未知数,且未知数的次数是2的方程(a≠0);得到m2-2=2且m-2≠0,求出m的值.
17.【答案】-3
【考点】一元二次方程的定义及相关的量
【解析】【解答】解:由一元二次方程的特点得m2-7=2,即m=±3,m=3舍去,即m=-3时,原方程是一元二次方程.
故答案为:-3.【分析】根据一元二次方程的定义可得m2-7=2,且m-3≠0,从而求出符合条件的m值.
18.【答案】
【考点】配方法解一元二次方程
【解析】【解答】解:一元二次方程x2-6x-5=0通过配方可变形为
故答案为:
【分析】先将常数项移到方程的右边,再在方程两边同时加上一次项系数一半的平方,即可得出答案。
19.【答案】12
【考点】因式分解法解一元二次方程,三角形三边关系
【解析】【解答】解:由方程(x﹣2)(x﹣5)=0可得x﹣2=0或x﹣5=0,
解得:x=2或x=5,
当三角形的三边为2、2、5时,2+2<5,不能构成三角形,舍去;
当三角形的三边为2、5、5时,2+5>5,可以构成三角形,其周长为2+5+5=12,
故答案为:12.
【分析】根据因式分解法求出方程的解,根据等腰三角形的性质和根据两边之和大于第三边,两边之差小于第三边,求出等腰三角形的周长.
20.【答案】 ﹣1+
【考点】一元二次方程根的判别式及应用,一元二次方程的根与系数的关系
【解析】【解答】解:设方程x2+(2k+1)x+k2=0的两个实数根分别为m、n,
则有:m+n=﹣2k﹣1,mn=k2 ,
∵m2+n2=(m+n)2﹣2mn=11,
∴(﹣2k﹣1)2﹣2k2=11,即k2+2k﹣5=0,
解得:k=﹣1﹣ 或k=﹣1+ .
∵方程有实数根,
∴△=(2k+1)2﹣4k2=4k+1≥0,
∴k≥﹣ ,
∴k=﹣1+ .
故答案为:﹣1+ .
【分析】设方程x2+(2k+1)x+k2=0的两个实数根分别为m、n,根据根与系数的关系可得出m+n=﹣2k﹣1、mn=k2 , 结合m2+n2=11即可得出关于k的一元二次方程,解方程可得出k的值,再根据方程有解结合根的判别式即可得出关于k的一元一次不等式,解不等式可得出k的取值范围,由此即可确定k的值.
21.【答案】
【考点】根的判别式
【解析】【解答】由题意得 ?,解得 .
故答案为:0 ≤ m ≤ 4 3 且 m ≠ 1 ?.
【分析】本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解答此题的关键.
27.【答案】 (1)解:原方程可化为: ,两边开平方得: ,
∴
(2)解:因式分解得: ,∴
(3)解:∵ ,
∴
【考点】直接开平方法解一元二次方程,配方法解一元二次方程,因式分解法解一元二次方程
【解析】【分析】(1)利用直接开平方法求出方程的解即可。
(2)观察方程的特点:右边为0,左边可以分解因式,因此利用因式分解法解方程。
(3)利用公式法解方程即可。
三、计算题
22.【答案】解:2x2-4x+5=0,
∵a=2,b=-4,c=5,∴b2-4ac=(-4)2-4×2×5=-24<0,
∴该方程没有实数根
【考点】根的判别式
【解析】【分析】由题意有a=2,b=-4,c=5,所以b2-4ac=(-4)2-4×2×5=-24<0,根据一元二次方程的根与系数的关系可得方程没有实数根。
23.【答案】解:移项得:
原方程无解
【考点】一元二次方程根的判别式及应用
【解析】【分析】先将方程化为一般形式,?x2? 3x?8=0,所以a=1,b=?3,c=8,
b2?4ac=9?4×1×8=?23<0,根据一元二次方程的根的判别式可知原方程无实数根。
三、解答题
24.【答案】解:|2a+3|=2
2a+3=±2
当 时,
当 时
【考点】一元二次方程的定义,解一元二次方程-公式法
【解析】【分析】根据一元二次方程的定义可得|2a+3|=2,且a+1不为0,解得 , 再将a = - 或 a = - 代入原方程即可求解。
25.【答案】解:∵x2﹣3x﹣4=0,
∴x=4或x=﹣1(舍),
∵菱形的边长是5cm,
∴菱形的另外一条对角线=2 ?=6cm,
∴菱形的面积为= ×6×8=24cm2
【考点】因式分解法解一元二次方程,菱形的性质
【解析】【分析】先解一元二次方程,那么一元二次方程的正跟即为菱形另一条对角线的一半长,那么菱形的面积即为两条对角线长度积的一半.
26.【答案】 解:∵a=1,b=-2m,c=m2-2,
∴ ,
∴ ,
【考点】公式法解一元二次方程
【解析】【分析】由题意有,a=1,b=-2m,c=m2-2,所以根据一元二次方程的求根公式x=求解即可。
25.【答案】(1)解:由判别式可得(m+2)2-4(2m-1)=m2+4m+4-8m+4= m2-4m+8=(m-2)2+4>0.
所以方程恒有两个不相等的实数根。
(2)解:把x=1代入方程可得1-(m+2)+(2m-1)=0,解得m=2,
把m=2代入方程可整理得x2-4x+3=0,解得x1=1,x2=3.
当1和3都是直角边的边长时,斜边长为 ,周长为4+ 。
当3是斜边长时,另一条边长是 ,周长为4+ 。
【考点】根的判别式
【解析】【分析】(1)方程的解与根的判别式有关,求出判别式的范围,再判断根的情况;(2)由于方程中有个未知数m,可以将x=1代入方程先求出m的解;再将m的值代入,解出一元二次方程的两个解,则分类讨论两个解分别是直角边还是斜边,求出第三条边,写出周长。
27.【答案】(1)解:△ABC是等腰三角形.理由如下:
将x=-1代入方程得a+c-2b+a-c=0,
即a=b,
则△ABC是等腰三角形.
(2)解:△ABC是直角三角形.理由如下:
判别式=(2b)2-4(a+c)(a-c)=4b2-4a2+4c2=4(b2-a2-c2)=0,
即b2=a2+c2.
则△ABC是直角三角形
(3)解:∵△ABC是等边三角形,
∴a=b=c,
∴方程可化为2ax2+2ax+=0,
∴2ax(x+1)=0,
∴x1=0,x2=-1.
【考点】根的判别式,一元二次方程的应用
【解析】【分析】(1)将x=-1的值代入,整理方程可得a,b,c的数量关系;
(2)根据判别式=b2-4ac=0,整理可得a,b,c的数量关系;
(3)根据a=b=c代入方程可解得方程的解.
1 / 1
