人教A版必修一:3.2.1 几类不同增长的函数模型 课件(共17张PPT)
文档属性
| 名称 | 人教A版必修一:3.2.1 几类不同增长的函数模型 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 322.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 07:52:47 | ||
图片预览



文档简介
3.2.1 几类不同增长的函数模型
第二课时 幂、指、对函数模型 增长的差异性
问题提出
1.指数函数y=ax (a>1),对数函数 y=logax(a>1)和幂函数y=x n (n>0)在区间(0,+∞)上的单调性如何?
2.利用这三类函数模型解决实际问题,其增长速度是有差异的,我们怎样认识这种差异呢?
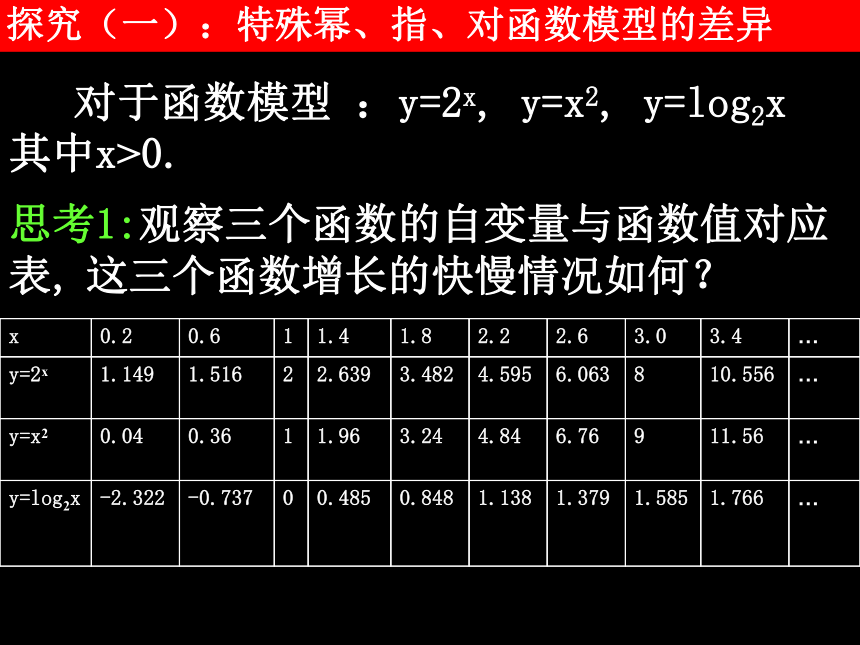
探究(一):特殊幂、指、对函数模型的差异
对于函数模型 :y=2x, y=x2, y=log2x 其中x>0.
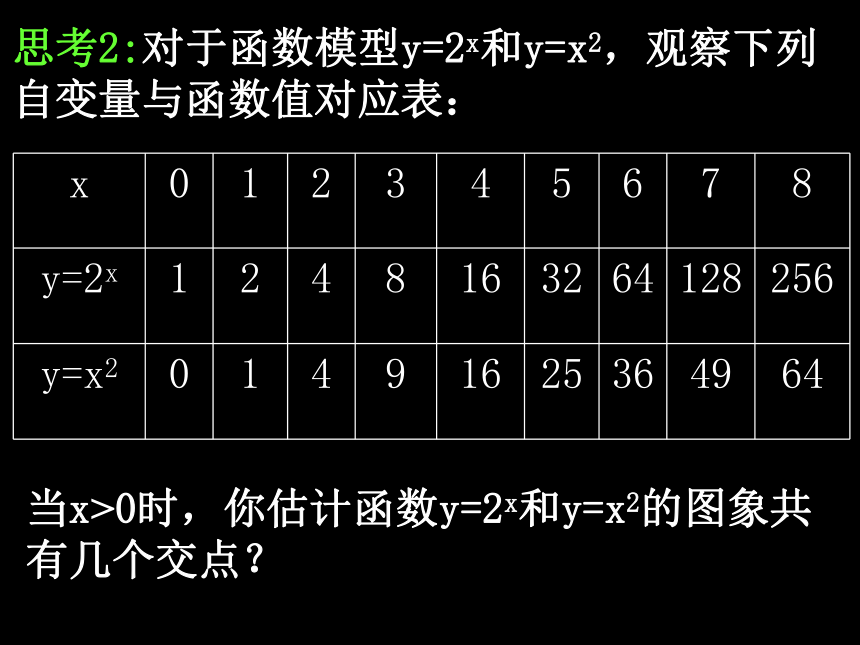
思考2:对于函数模型y=2x和y=x2,观察下列自变量与函数值对应表:
当x>0时,你估计函数y=2x和y=x2的图象共有几个交点?
x 0 1 2 3 4 5 6 7 8
y=2x 1 2 4 8 16 32 64 128 256
y=x2 0 1 4 9 16 25 36 49 64
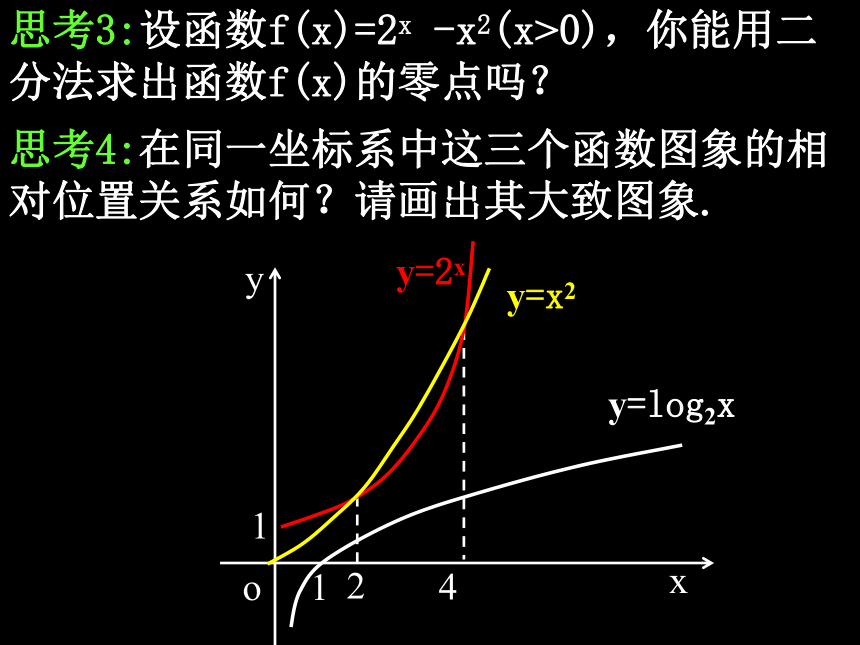
思考4:在同一坐标系中这三个函数图象的相对位置关系如何?请画出其大致图象.
思考3:设函数f(x)=2x -x2(x>0),你能用二分法求出函数f(x)的零点吗?
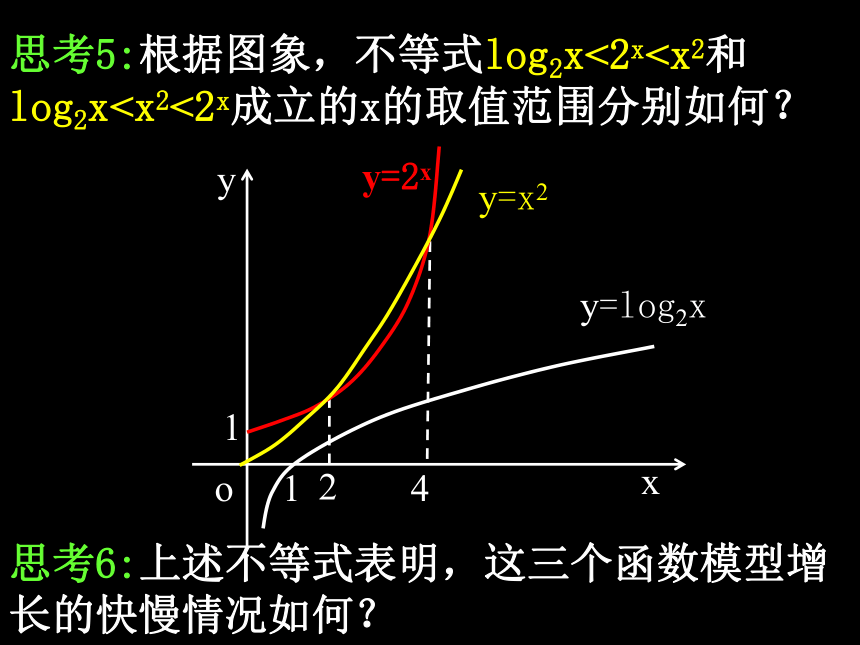
思考5:根据图象,不等式log2x<2xlog2x思考6:上述不等式表明,这三个函数模型增长的快慢情况如何?
探究(二):一般幂、指、对函数模型的差异
思考1:对任意给定的a>1和n>0,在区间(0,+∞) 上ax是否恒大于xn? ax是否恒小于xn?
思考2:当a>1,n>0时,在区间(0,+∞)上, ax 与xn的大小关系应如何阐述?
思考3:一般地,指数函数y=ax (a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,其增长的快慢情况是如何变化的?
当自变量X越来越大时,可以看出指数函数图像就像与X轴垂直一样,它的值快速增长,二次函数比起指数函数来几乎微不足道的
在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
结论1:
一般地,对于指数函数y=ax (a>1)和幂函数y=xn (n>0),通过探索可以发现:
在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
思考4:对任意给定的a>1和n>0,在区间 (0,+∞)上,logax是否恒大于xn? logax是否恒小于xn?
思考5:随着x的增大,logax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化?
思考6:当x充分大时,logax(a>1)xn与(n>0)谁的增长速度相对较快?
思考7:一般地,对数函数y=logax(a>1)和幂函数y=xn(n>0) 在区间(0,+∞)上,其增长的快慢情况如何是如何变化的?
结论2:
一般地,对于指数函数y=logax (a>1)和幂函数y=xn (n>0),通过探索可以发现:
在区间(0,+∞)上,随着x的增大,logax增大得越来越慢,图象就像是渐渐地与x轴平行一样。尽管在x的一定范围内, logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax思考8:对于指数函数y=ax(a>1),对数函数 y=logax(a>1)和幂函数y=xn(n>0),总存在一个x0,使x>x0时,ax,logax,xn三者的大小关系如何?
综上所述:
(1)、在区间(0,+∞)上,y=ax (a>1),y=logax (a>1)和y=xn (n>0)都是增函数。
(2)、随着x的增大, y=ax (a>1)的增长速度越来越快,会远远大于y=xn (n>0)的增长速度。
(3)、随着x的增大, y=logax (a>1)的增长速度越来越慢,会远远小于y=xn (n>0)的增长速度。
总存在一个x0,当x>x0时,就有
logax思考9:指数函数y=ax (0理论迁移
例 在某种金属材料的耐高温实验中,温度y(°C)随着时间t(分钟)的变化情况,由微机处理后显示出如下图象,试对该实验现象作出合理解释.
小结作业
P101练习:1.
P107习题3.2A组:3.
第二课时 幂、指、对函数模型 增长的差异性
问题提出
1.指数函数y=ax (a>1),对数函数 y=logax(a>1)和幂函数y=x n (n>0)在区间(0,+∞)上的单调性如何?
2.利用这三类函数模型解决实际问题,其增长速度是有差异的,我们怎样认识这种差异呢?
探究(一):特殊幂、指、对函数模型的差异
对于函数模型 :y=2x, y=x2, y=log2x 其中x>0.
思考2:对于函数模型y=2x和y=x2,观察下列自变量与函数值对应表:
当x>0时,你估计函数y=2x和y=x2的图象共有几个交点?
x 0 1 2 3 4 5 6 7 8
y=2x 1 2 4 8 16 32 64 128 256
y=x2 0 1 4 9 16 25 36 49 64
思考4:在同一坐标系中这三个函数图象的相对位置关系如何?请画出其大致图象.
思考3:设函数f(x)=2x -x2(x>0),你能用二分法求出函数f(x)的零点吗?
思考5:根据图象,不等式log2x<2x
探究(二):一般幂、指、对函数模型的差异
思考1:对任意给定的a>1和n>0,在区间(0,+∞) 上ax是否恒大于xn? ax是否恒小于xn?
思考2:当a>1,n>0时,在区间(0,+∞)上, ax 与xn的大小关系应如何阐述?
思考3:一般地,指数函数y=ax (a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,其增长的快慢情况是如何变化的?
当自变量X越来越大时,可以看出指数函数图像就像与X轴垂直一样,它的值快速增长,二次函数比起指数函数来几乎微不足道的
在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
结论1:
一般地,对于指数函数y=ax (a>1)和幂函数y=xn (n>0),通过探索可以发现:
在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
思考4:对任意给定的a>1和n>0,在区间 (0,+∞)上,logax是否恒大于xn? logax是否恒小于xn?
思考5:随着x的增大,logax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化?
思考6:当x充分大时,logax(a>1)xn与(n>0)谁的增长速度相对较快?
思考7:一般地,对数函数y=logax(a>1)和幂函数y=xn(n>0) 在区间(0,+∞)上,其增长的快慢情况如何是如何变化的?
结论2:
一般地,对于指数函数y=logax (a>1)和幂函数y=xn (n>0),通过探索可以发现:
在区间(0,+∞)上,随着x的增大,logax增大得越来越慢,图象就像是渐渐地与x轴平行一样。尽管在x的一定范围内, logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax
综上所述:
(1)、在区间(0,+∞)上,y=ax (a>1),y=logax (a>1)和y=xn (n>0)都是增函数。
(2)、随着x的增大, y=ax (a>1)的增长速度越来越快,会远远大于y=xn (n>0)的增长速度。
(3)、随着x的增大, y=logax (a>1)的增长速度越来越慢,会远远小于y=xn (n>0)的增长速度。
总存在一个x0,当x>x0时,就有
logax
例 在某种金属材料的耐高温实验中,温度y(°C)随着时间t(分钟)的变化情况,由微机处理后显示出如下图象,试对该实验现象作出合理解释.
小结作业
P101练习:1.
P107习题3.2A组:3.
