高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件 新人教B版选修2_1(44张PPT)
文档属性
| 名称 | 高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件 新人教B版选修2_1(44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 08:18:14 | ||
图片预览







文档简介
课件44张PPT。空间向量证明
立体几何问题空间
向量空间
向量
的运
算空间
向量
基本
定理空间
向量
的坐
标运
算加减
和数
乘运
算共线
向量
共面
向量空间
向量
的数
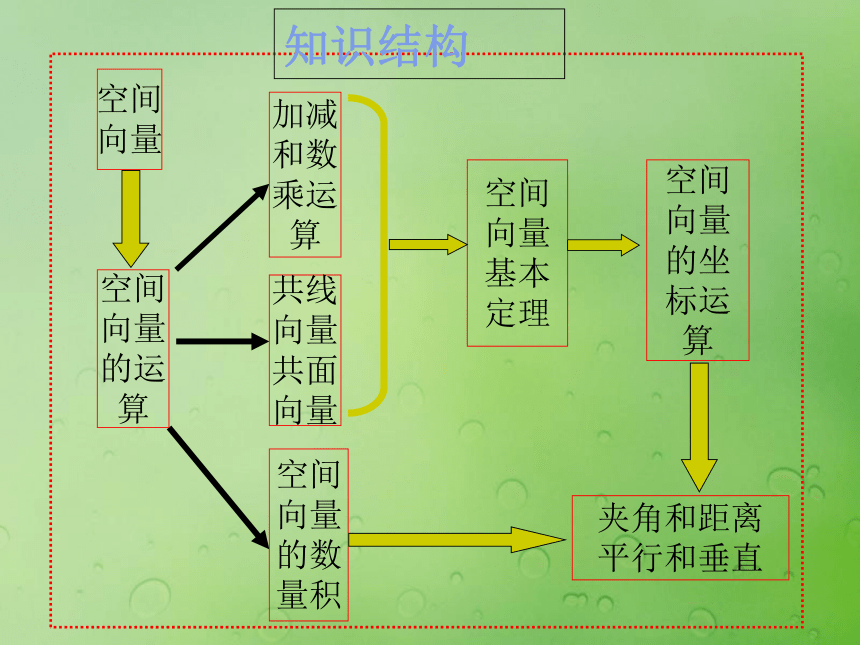
量积知识结构夹角和距离
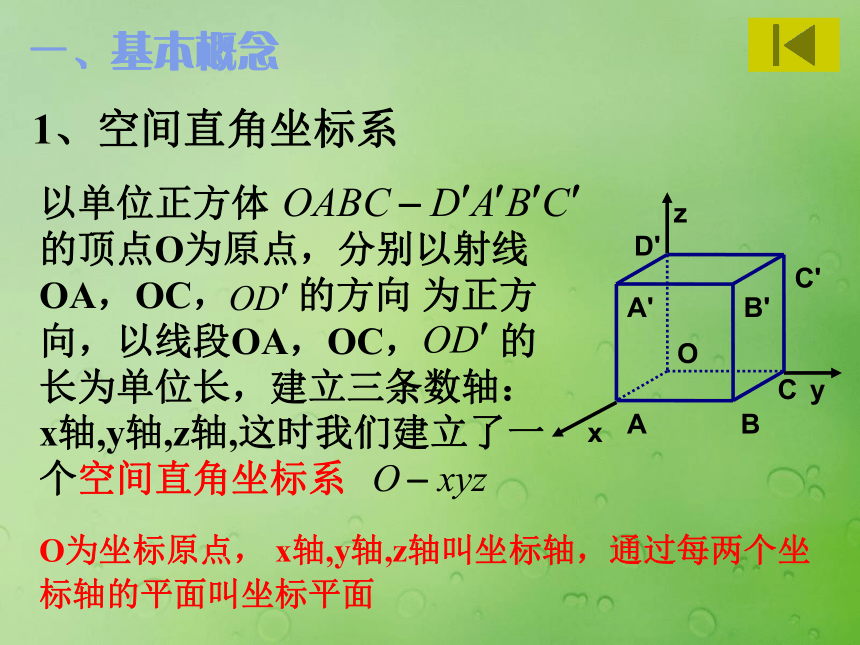
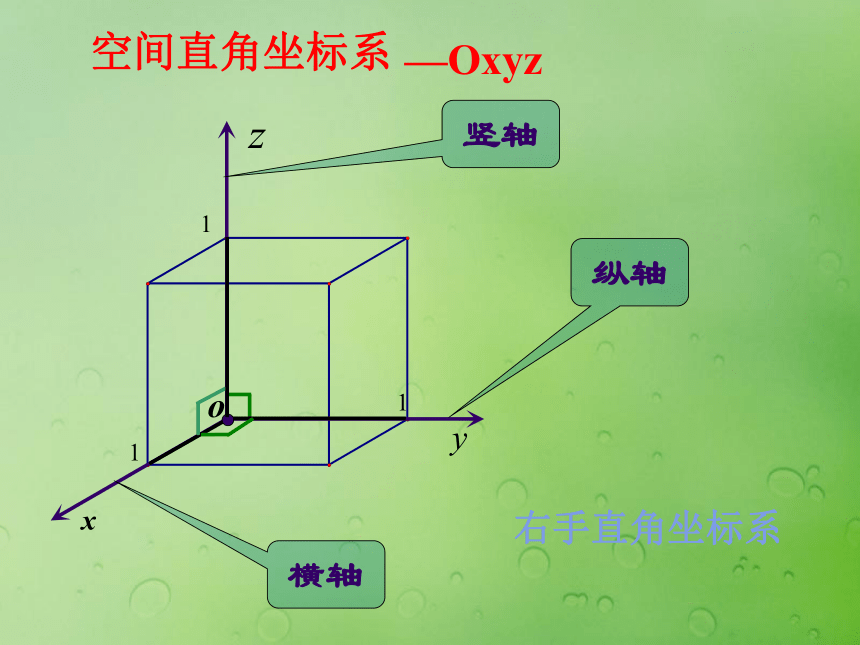
平行和垂直1、空间直角坐标系以单位正方体 的顶点O为原点,分别以射线OA,OC, 的方向 为正方向,以线段OA,OC, 的长为单位长,建立三条数轴:x轴,y轴,z轴,这时我们建立了一个空间直角坐标系BO为坐标原点, x轴,y轴,z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面一、基本概念右手直角坐标系横轴纵轴竖轴2、空间直角坐标系中点的坐标有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标,记作M(x,y,z)其中x叫做点M的横坐标,y叫做点M的纵坐标, z叫做点M的竖坐标 如果表示向量n的有向线段所在的直线垂直于平面α,称这个向量垂直于平面α,记作n⊥α,这时向量n叫做平面α的法向量. 4、平面的法向量3、直线的方向向量1、假设平面法向量的坐标为n=(x,y,z).
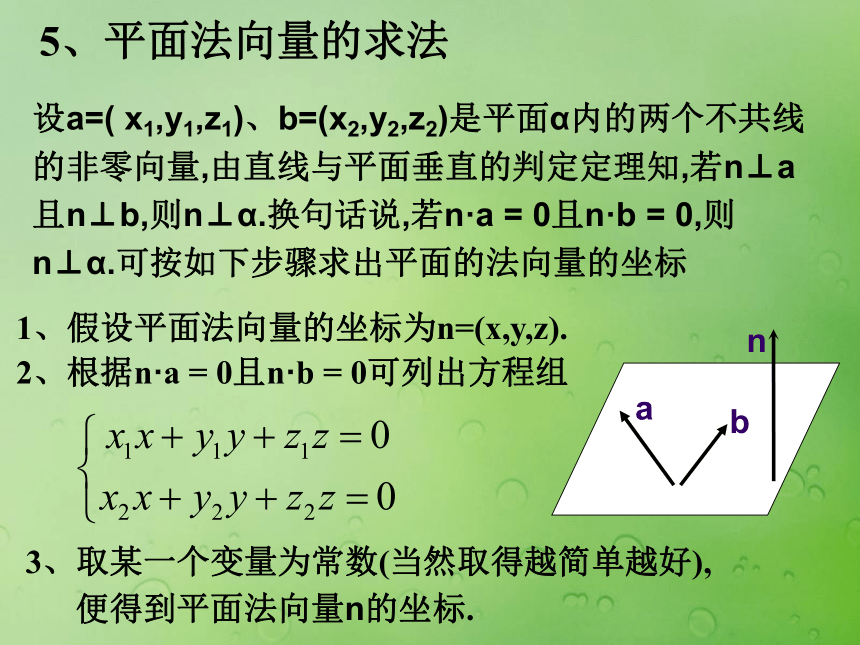
2、根据n·a = 0且n·b = 0可列出方程组3、取某一个变量为常数(当然取得越简单越好),
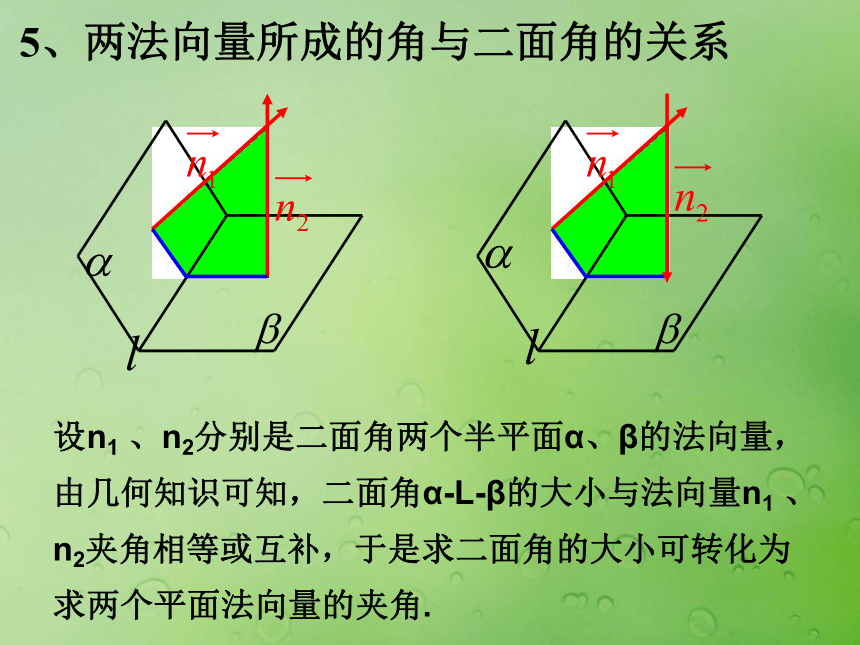
便得到平面法向量n的坐标. 5、平面法向量的求法设a=( x1,y1,z1)、b=(x2,y2,z2)是平面α内的两个不共线的非零向量,由直线与平面垂直的判定定理知,若n⊥a且n⊥b,则n⊥α.换句话说,若n·a = 0且n·b = 0,则n⊥α.可按如下步骤求出平面的法向量的坐标例、已知A(2,1,1),B(-2,7,0),C(6,4,-1).求平面ABC的法向量解:平面ABC的法向量为: 例、在棱长为2的正方体ABCD-A1B1C1D1中,O是面AC的中心,求面OA1D1的法向量.解:以A为原点建立空间直角坐标系O-xyz(如图),
则O(1,1,0),A1(0,0,2),D1(0,2,2),
设平面OA1D1的法向量的法向量为n=(x,y,z),
由 =(-1,-1,2), =(-1,1,2)得 解得取z =1得平面OA1D1的法向量的坐标n=(2,0,1)5、两法向量所成的角与二面角的关系设n1 、n2分别是二面角两个半平面α、β的法向量,由几何知识可知,二面角α-L-β的大小与法向量n1 、n2夹角相等或互补,于是求二面角的大小可转化为求两个平面法向量的夹角.二、基本公式:1、两点间的距离公式(线段的长度)2、向量的长度公式(向量的模)3、向量的坐标运算公式4、两个向量平行的条件5、两个向量垂直的条件或7、重心坐标公式6、中点坐标公式9、直线与平面所成角公式8、直线与直线所成角公式 10、平面与平面所成角公式 ( 为二面角两个半平面的法向量)11、点到平面的距离公式(PM为平面 的斜线, 为平面 的法向量)12、异面直线的距离公式(A,B为异面直线上两点, 为公垂线的方向向量)利用向量求角直线与直线所成的角直线与平面所成的角平面与平面所成的角(二面角)利用向量求距离点到直线的距离点到平面的距离直线到平面的距离平行到平面的距离直线到直线的距离三、基本应用利用向量证平行利用向量证垂直直线与直线垂直直线与平面垂直平面与平面垂直直线与直线平行直线与平面平行平面与平面平行2、垂直问题四、基本方法1、平行问题3、角度问题4、距离问题(1)点到点的距离、点到平面的距离、直线到直线的距离直接用公式求解。(2)点到直线的距离、直线到平面的距离、平面到平面的距离转化为点到平面的距离求解。例:五、典型例题所以:解:以点C 为坐标原点建立空间
直角坐标系 如图所示,
不妨设 则 C所以 与 所成角的余弦值为N解:如图建立坐标系A-xyz,则N又例.在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EEFEXYZ或先求平面BDE的法向量 再证明设平面XYZ例:在正方体ABCD-A1B1C1D1中,求证:面A1BD∥面CB1D1或先求两平面的法向量 再证明例、在正方体AC1中,E、F分别是BB1、CD的中点,
求证:面AED⊥面A1FD1ABCDA1B1C1D1EF或证明两平面的法向量垂直练习练习练习练习练习ABCC1取x=1,z则y=-1,z=1,所以EA1B1ABCDEFGXYZ练习练习练习练习 已知正方形ABCD的边长为1,PD 平面ABCD,且PD=1,E、F分别为AB、BC的中点。
求证:PE AF;
求点D到平面PEF的距离;
求直线AC到平面PEF的距离;
求直线PA与EF的距离;
求直线PA与EF所成的角;
求PA与平面PEF所成的角;
求二面角A-PE-F的大小。练习
立体几何问题空间
向量空间
向量
的运
算空间
向量
基本
定理空间
向量
的坐
标运
算加减
和数
乘运
算共线
向量
共面
向量空间
向量
的数
量积知识结构夹角和距离
平行和垂直1、空间直角坐标系以单位正方体 的顶点O为原点,分别以射线OA,OC, 的方向 为正方向,以线段OA,OC, 的长为单位长,建立三条数轴:x轴,y轴,z轴,这时我们建立了一个空间直角坐标系BO为坐标原点, x轴,y轴,z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面一、基本概念右手直角坐标系横轴纵轴竖轴2、空间直角坐标系中点的坐标有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标,记作M(x,y,z)其中x叫做点M的横坐标,y叫做点M的纵坐标, z叫做点M的竖坐标 如果表示向量n的有向线段所在的直线垂直于平面α,称这个向量垂直于平面α,记作n⊥α,这时向量n叫做平面α的法向量. 4、平面的法向量3、直线的方向向量1、假设平面法向量的坐标为n=(x,y,z).
2、根据n·a = 0且n·b = 0可列出方程组3、取某一个变量为常数(当然取得越简单越好),
便得到平面法向量n的坐标. 5、平面法向量的求法设a=( x1,y1,z1)、b=(x2,y2,z2)是平面α内的两个不共线的非零向量,由直线与平面垂直的判定定理知,若n⊥a且n⊥b,则n⊥α.换句话说,若n·a = 0且n·b = 0,则n⊥α.可按如下步骤求出平面的法向量的坐标例、已知A(2,1,1),B(-2,7,0),C(6,4,-1).求平面ABC的法向量解:平面ABC的法向量为: 例、在棱长为2的正方体ABCD-A1B1C1D1中,O是面AC的中心,求面OA1D1的法向量.解:以A为原点建立空间直角坐标系O-xyz(如图),
则O(1,1,0),A1(0,0,2),D1(0,2,2),
设平面OA1D1的法向量的法向量为n=(x,y,z),
由 =(-1,-1,2), =(-1,1,2)得 解得取z =1得平面OA1D1的法向量的坐标n=(2,0,1)5、两法向量所成的角与二面角的关系设n1 、n2分别是二面角两个半平面α、β的法向量,由几何知识可知,二面角α-L-β的大小与法向量n1 、n2夹角相等或互补,于是求二面角的大小可转化为求两个平面法向量的夹角.二、基本公式:1、两点间的距离公式(线段的长度)2、向量的长度公式(向量的模)3、向量的坐标运算公式4、两个向量平行的条件5、两个向量垂直的条件或7、重心坐标公式6、中点坐标公式9、直线与平面所成角公式8、直线与直线所成角公式 10、平面与平面所成角公式 ( 为二面角两个半平面的法向量)11、点到平面的距离公式(PM为平面 的斜线, 为平面 的法向量)12、异面直线的距离公式(A,B为异面直线上两点, 为公垂线的方向向量)利用向量求角直线与直线所成的角直线与平面所成的角平面与平面所成的角(二面角)利用向量求距离点到直线的距离点到平面的距离直线到平面的距离平行到平面的距离直线到直线的距离三、基本应用利用向量证平行利用向量证垂直直线与直线垂直直线与平面垂直平面与平面垂直直线与直线平行直线与平面平行平面与平面平行2、垂直问题四、基本方法1、平行问题3、角度问题4、距离问题(1)点到点的距离、点到平面的距离、直线到直线的距离直接用公式求解。(2)点到直线的距离、直线到平面的距离、平面到平面的距离转化为点到平面的距离求解。例:五、典型例题所以:解:以点C 为坐标原点建立空间
直角坐标系 如图所示,
不妨设 则 C所以 与 所成角的余弦值为N解:如图建立坐标系A-xyz,则N又例.在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EEFEXYZ或先求平面BDE的法向量 再证明设平面XYZ例:在正方体ABCD-A1B1C1D1中,求证:面A1BD∥面CB1D1或先求两平面的法向量 再证明例、在正方体AC1中,E、F分别是BB1、CD的中点,
求证:面AED⊥面A1FD1ABCDA1B1C1D1EF或证明两平面的法向量垂直练习练习练习练习练习ABCC1取x=1,z则y=-1,z=1,所以EA1B1ABCDEFGXYZ练习练习练习练习 已知正方形ABCD的边长为1,PD 平面ABCD,且PD=1,E、F分别为AB、BC的中点。
求证:PE AF;
求点D到平面PEF的距离;
求直线AC到平面PEF的距离;
求直线PA与EF的距离;
求直线PA与EF所成的角;
求PA与平面PEF所成的角;
求二面角A-PE-F的大小。练习
