高中数学人教A版选修2-1 3.2 立体几何中的向量方法 课件(21张)
文档属性
| 名称 | 高中数学人教A版选修2-1 3.2 立体几何中的向量方法 课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 08:19:33 | ||
图片预览





文档简介
课件21张PPT。3.2 立体几何中的向量方法(1)向量方法
的基本原理复习巩固①建系,求相关点的坐标;③运用向量运算解题.②求相关向量的坐标;1、运用向量的坐标运算解题的步骤:---这种解决问题的方法称为向量法中的坐标法问题提出 1.立体几何研究的主要问题有共点, 共线,共面,平行,垂直,夹角,距离等,这些问题都与空间向量有着密切的内在联系,从而可以用向量方法解决立体几何问题. 2.立体几何研究的基本对象是点、直线、平面以及由它们组成的空间图形.为了用空间向量解决立体几何问题,首先必须把点、直线、平面的位置用向量表示出来,然后再建立相应的解题原理. 3.上一节所学习的内容是空间向量的基础知识,如何利用这些基础知识解决立体几何中的实际问题,是本节学习的主体内容.向量方法
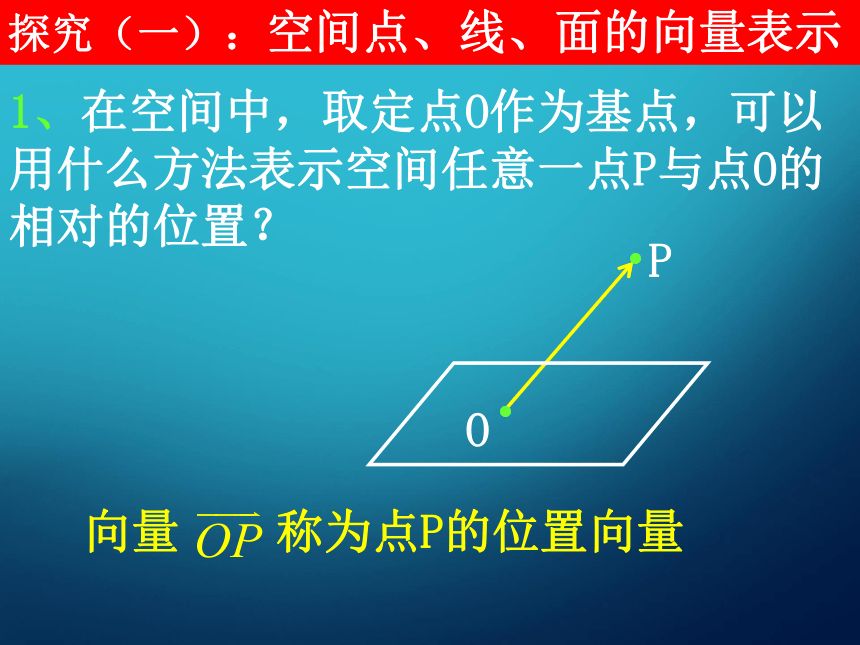
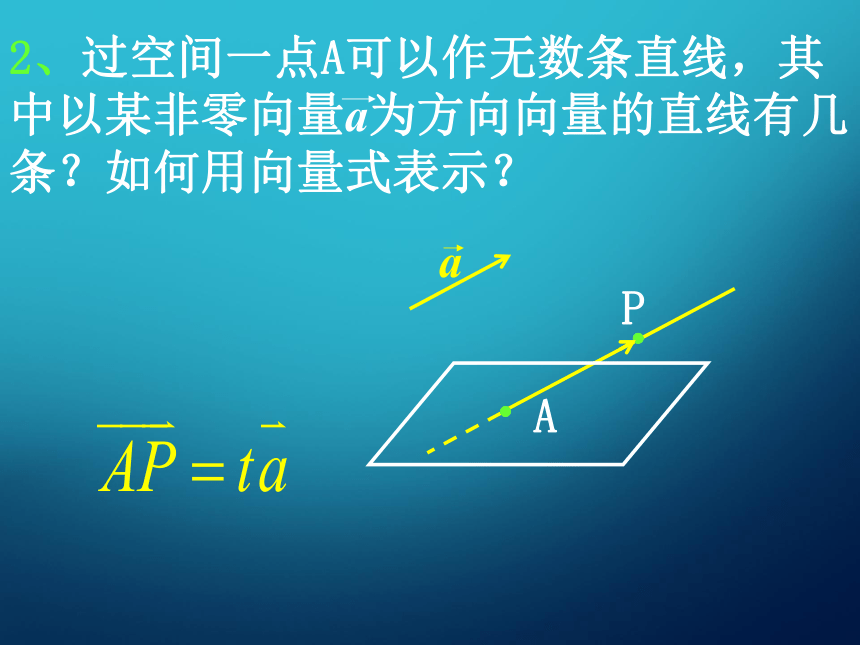
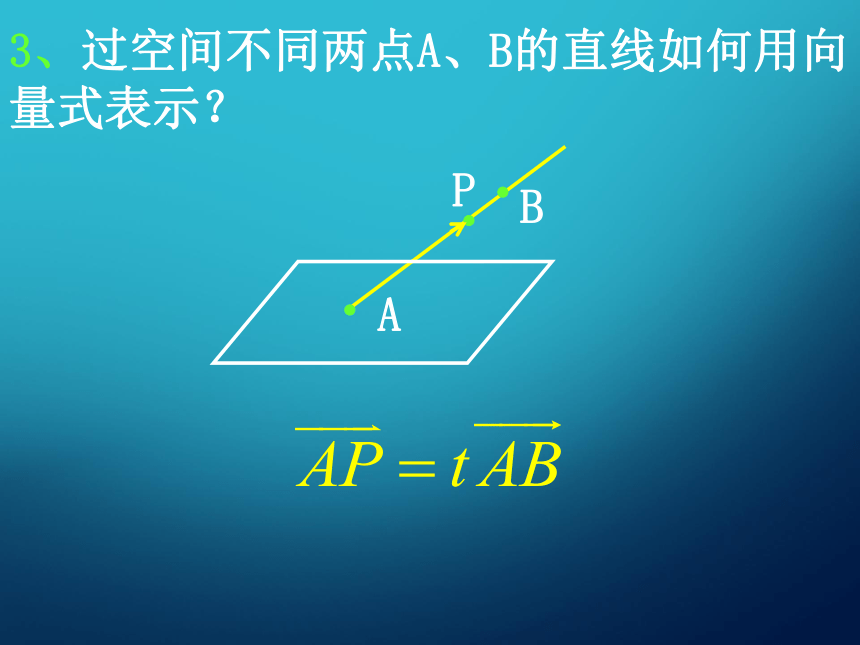
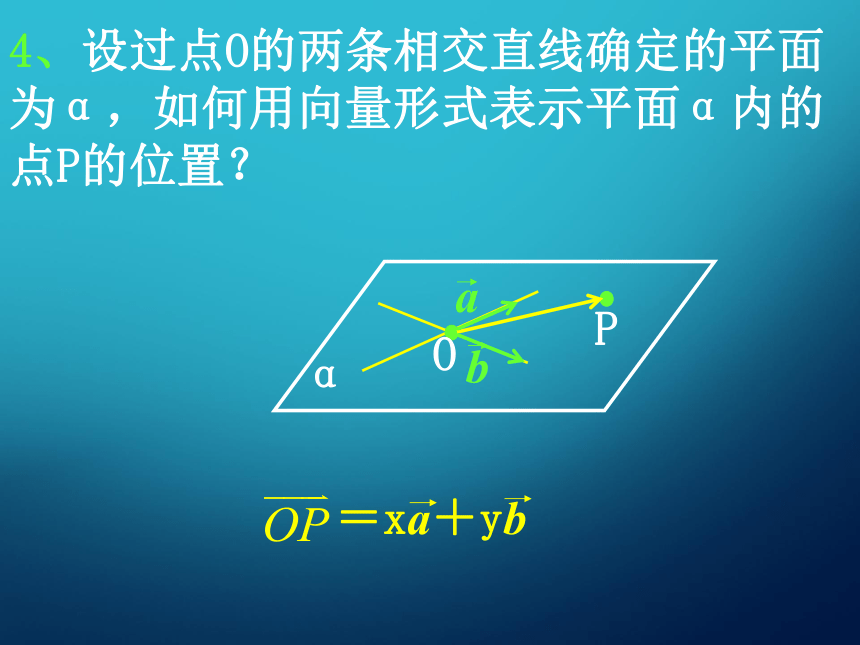
的基本原理探究(一):空间点、线、面的向量表示 2、过空间一点A可以作无数条直线,其中以某非零向量a为方向向量的直线有几条?如何用向量式表示?3、过空间不同两点A、B的直线如何用向量式表示? 4、设过点O的两条相交直线确定的平面为α,如何用向量形式表示平面α内的点P的位置? 5、若直线l⊥平面α,a为直线l的方向向量,则向量a叫做平面α的法向量,如何用向量形式表示过点O且法向量为a的平面α内的点P的位置? l探究(二):向量方法的基本原理 设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v. (1)、l//m,l//α,α//β的充要条件分别是什么?lmαl(1)、l//m,l//α,α//β的充要条件分别是什么?(1)、l//m,l//α,α//β的充要条
件分别是什么?(2)l⊥m,l⊥α,α⊥β的充要条件分别是什么?balmaα(2)l⊥m,l⊥α,α⊥β的充要条件分别是什么?l(2)l⊥m,l⊥α,α⊥β的充要条件分别是什么?3、直线l和m所成的角θ与向量a,b的关系如何? baαmlaα4、直线l和平面α所成的角θ与向量a,u的关系如何? l5、平面α和平面β所成的角θ与向量u,v的关系如何?理论迁移例1 求证:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. lm---这种解决问题的方法称为向量法 1.直线的方向向量和平面的法向量都不是惟一的,其方向有两种可能,其模可以为任意正数. 小结作业 2.设直线l的方向向量为a,对平面α内的任一向量p,若a·p=0,则l⊥α. 3.用向量方法研究与平面有关的问题时,一般利用平面的法向量进行运算.
的基本原理复习巩固①建系,求相关点的坐标;③运用向量运算解题.②求相关向量的坐标;1、运用向量的坐标运算解题的步骤:---这种解决问题的方法称为向量法中的坐标法问题提出 1.立体几何研究的主要问题有共点, 共线,共面,平行,垂直,夹角,距离等,这些问题都与空间向量有着密切的内在联系,从而可以用向量方法解决立体几何问题. 2.立体几何研究的基本对象是点、直线、平面以及由它们组成的空间图形.为了用空间向量解决立体几何问题,首先必须把点、直线、平面的位置用向量表示出来,然后再建立相应的解题原理. 3.上一节所学习的内容是空间向量的基础知识,如何利用这些基础知识解决立体几何中的实际问题,是本节学习的主体内容.向量方法
的基本原理探究(一):空间点、线、面的向量表示 2、过空间一点A可以作无数条直线,其中以某非零向量a为方向向量的直线有几条?如何用向量式表示?3、过空间不同两点A、B的直线如何用向量式表示? 4、设过点O的两条相交直线确定的平面为α,如何用向量形式表示平面α内的点P的位置? 5、若直线l⊥平面α,a为直线l的方向向量,则向量a叫做平面α的法向量,如何用向量形式表示过点O且法向量为a的平面α内的点P的位置? l探究(二):向量方法的基本原理 设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v. (1)、l//m,l//α,α//β的充要条件分别是什么?lmαl(1)、l//m,l//α,α//β的充要条件分别是什么?(1)、l//m,l//α,α//β的充要条
件分别是什么?(2)l⊥m,l⊥α,α⊥β的充要条件分别是什么?balmaα(2)l⊥m,l⊥α,α⊥β的充要条件分别是什么?l(2)l⊥m,l⊥α,α⊥β的充要条件分别是什么?3、直线l和m所成的角θ与向量a,b的关系如何? baαmlaα4、直线l和平面α所成的角θ与向量a,u的关系如何? l5、平面α和平面β所成的角θ与向量u,v的关系如何?理论迁移例1 求证:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. lm---这种解决问题的方法称为向量法 1.直线的方向向量和平面的法向量都不是惟一的,其方向有两种可能,其模可以为任意正数. 小结作业 2.设直线l的方向向量为a,对平面α内的任一向量p,若a·p=0,则l⊥α. 3.用向量方法研究与平面有关的问题时,一般利用平面的法向量进行运算.
