18.2.2 菱形(2)课件
图片预览

文档简介
人教版数学八年级下册
18.2.2菱形(2)
怎样判断一个四边形是菱形?
菱形ABCD的性质:
1.具有平行四边形的 一切性质。
2.菱形本身具有的特殊性质: 四条边相等;
两条对角线互相垂直平分, 每一条对角线平分一组对角.
3.菱形的面积等于菱形对角线乘积的一半.
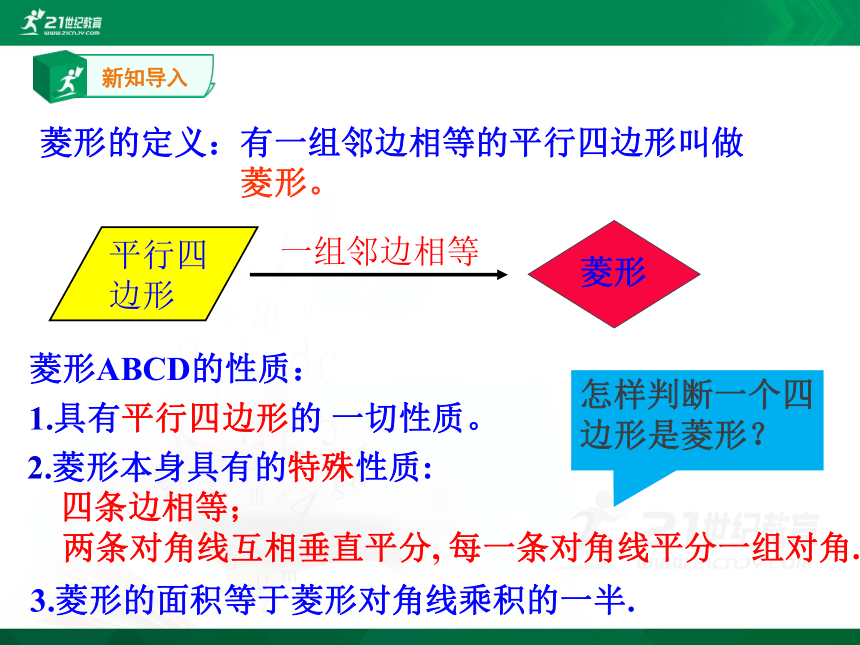
有一组邻边相等的平行四边形叫做菱形。
菱形的定义:
菱形
一组邻边相等
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
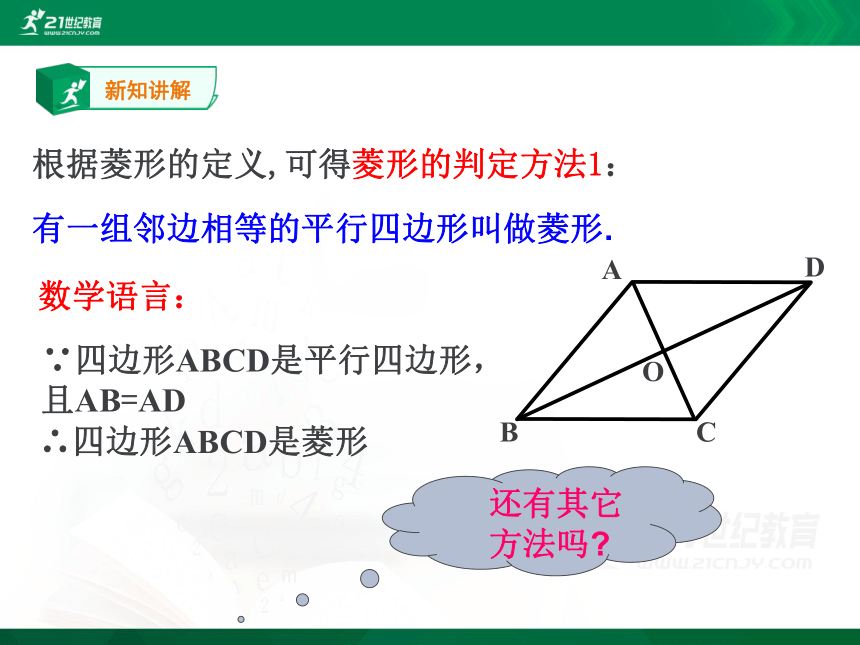
根据菱形的定义,可得菱形的判定方法1:
有一组邻边相等的平行四边形叫做菱形.
数学语言:
∵四边形ABCD是平行四边形,且AB=AD
∴四边形ABCD是菱形
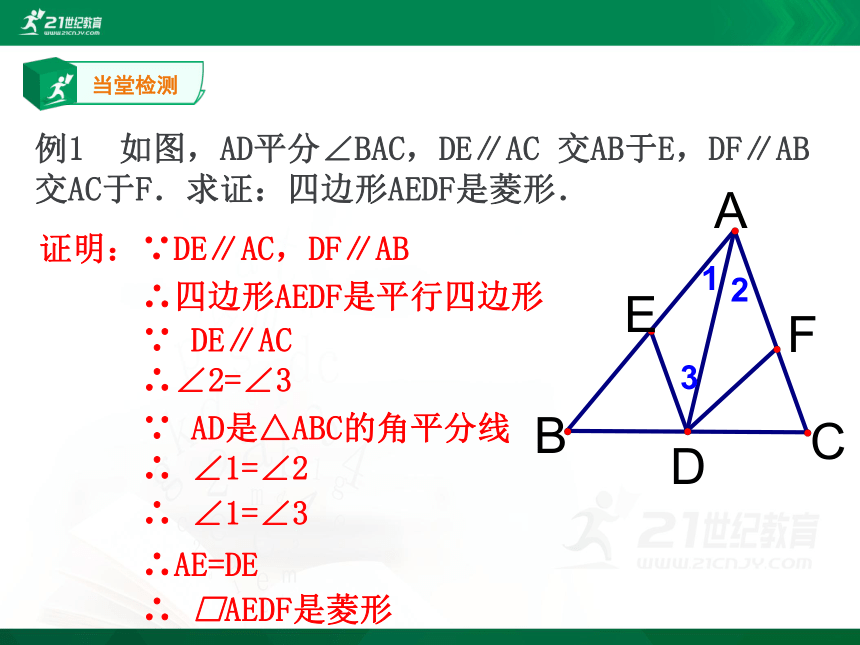
例1 如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形.
∴ □AEDF是菱形
证明:∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC
∴∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
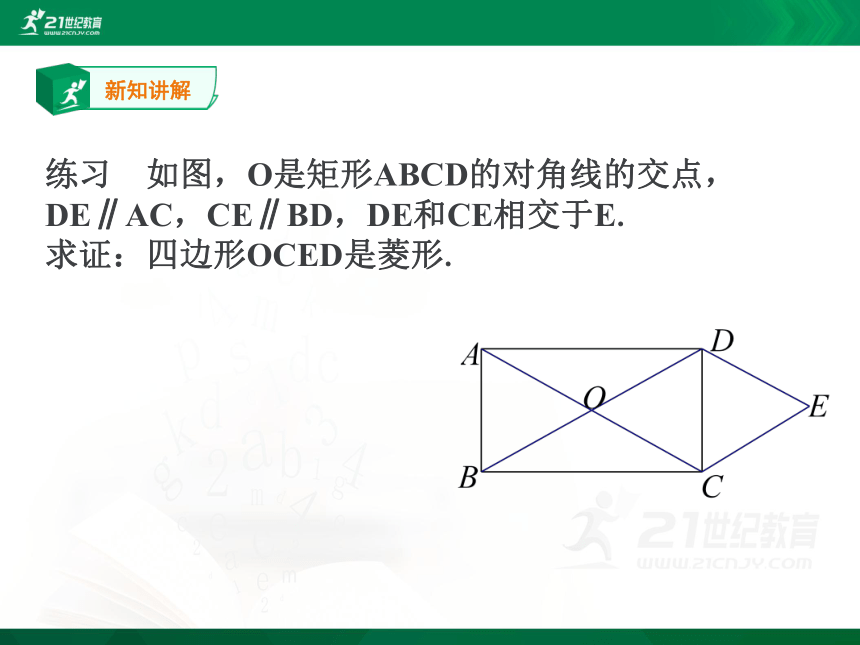
练习 如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E.
求证:四边形OCED是菱形.
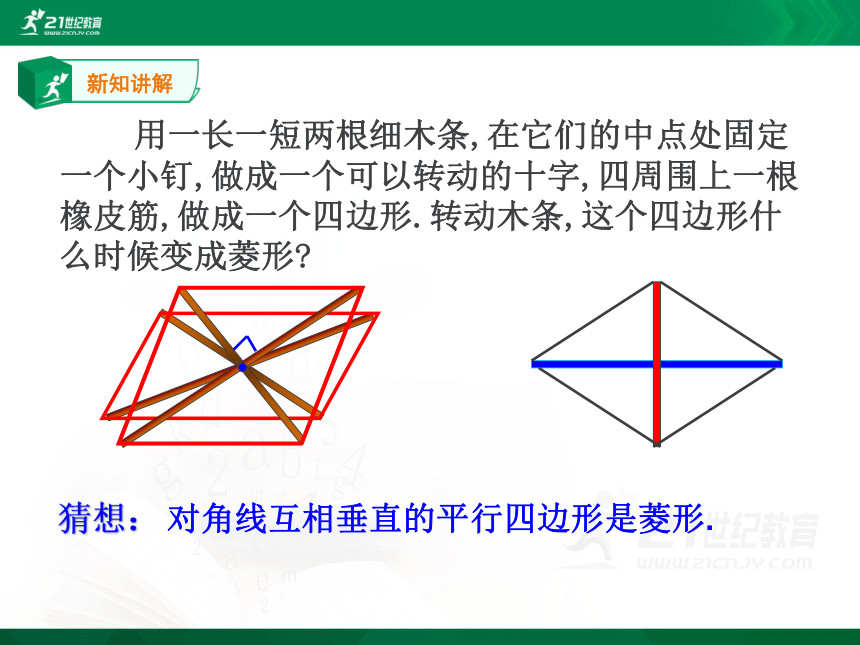
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
猜想:
对角线互相垂直的平行四边形是菱形.
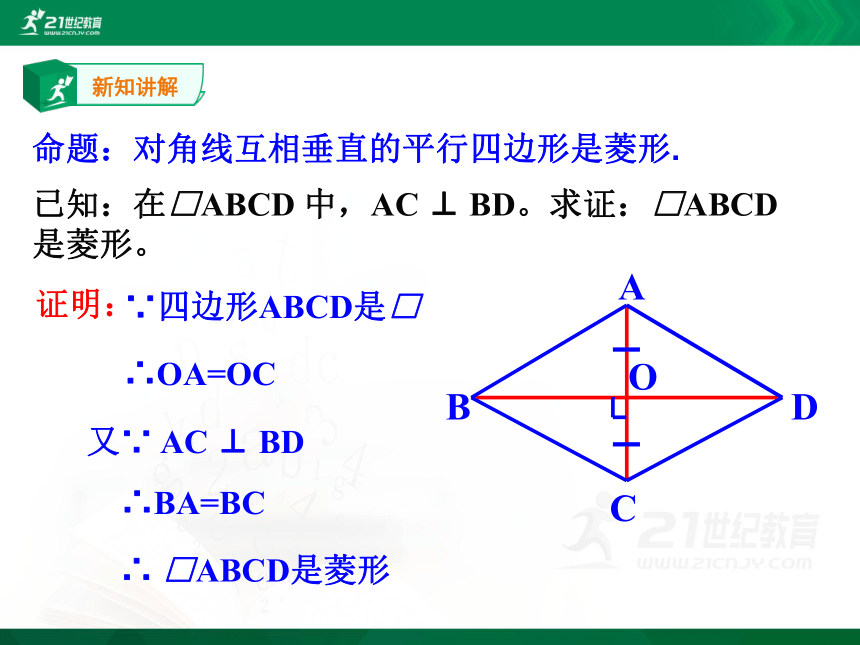
命题:对角线互相垂直的平行四边形是菱形.
已知:在□ABCD 中,AC ⊥ BD。求证:□ABCD是菱形。
证明:
∴ □ABCD是菱形
又∵ AC ⊥ BD
∵四边形ABCD是□
∴OA=OC
∴BA=BC
O
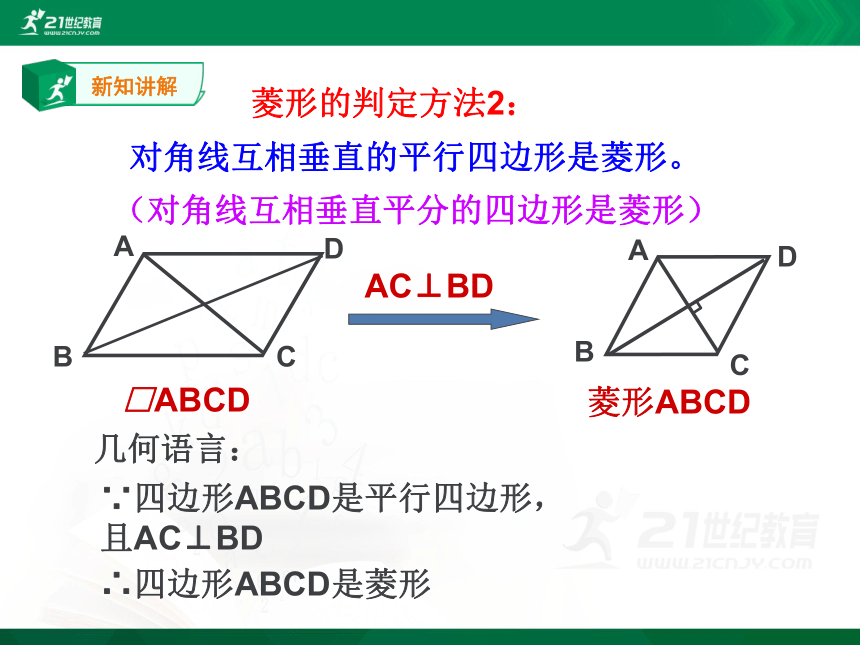
菱形的判定方法2:
对角线互相垂直的平行四边形是菱形。
∴四边形ABCD是菱形
(对角线互相垂直平分的四边形是菱形)
∵四边形ABCD是平行四边形,
且AC⊥BD
几何语言:
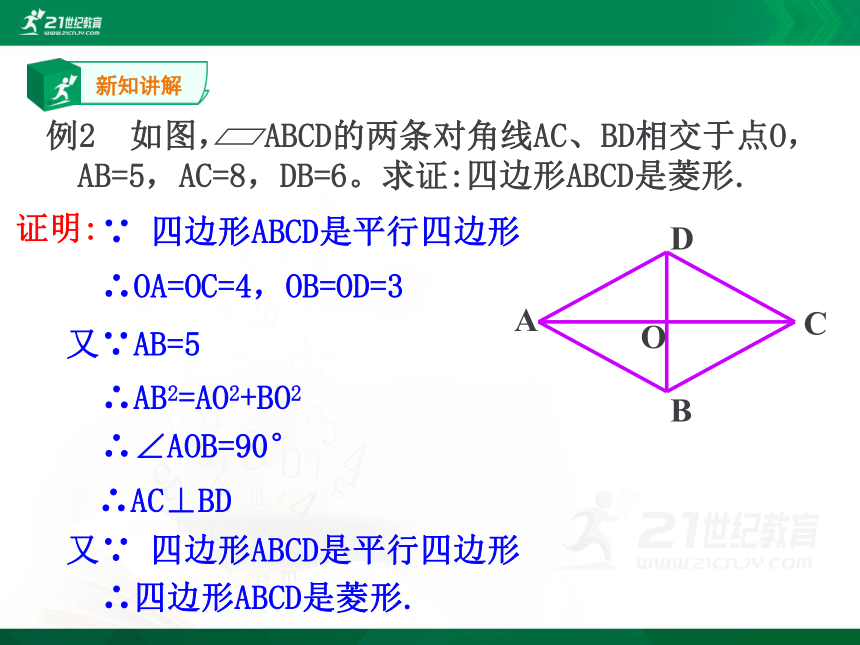
∴四边形ABCD是菱形.
∴OA=OC=4,OB=OD=3
证明:
又∵AB=5
∴AC⊥BD
∴∠AOB=90°
又∵ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
∴AB2=AO2+BO2
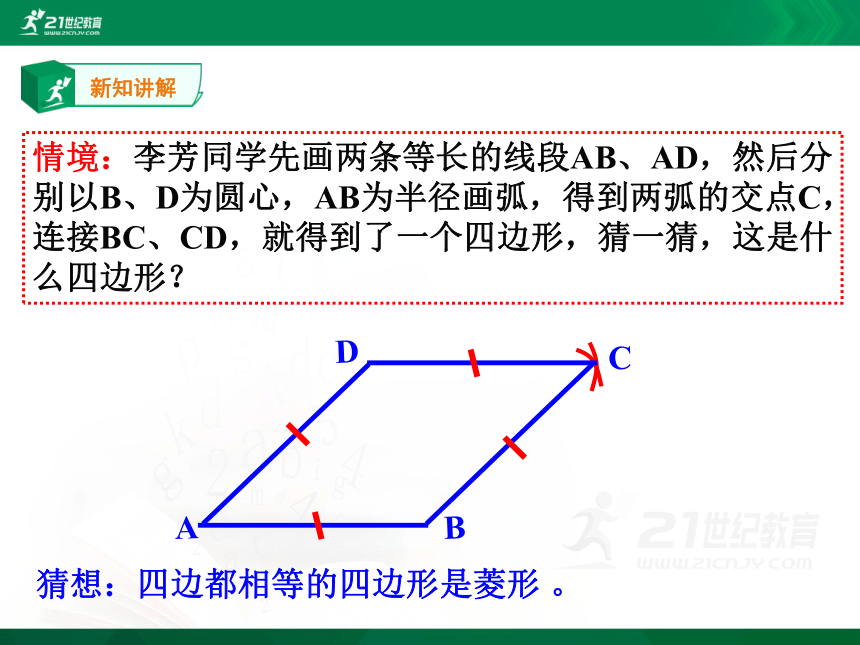
情境:李芳同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
猜想:四边都相等的四边形是菱形 。
A
B
C
D
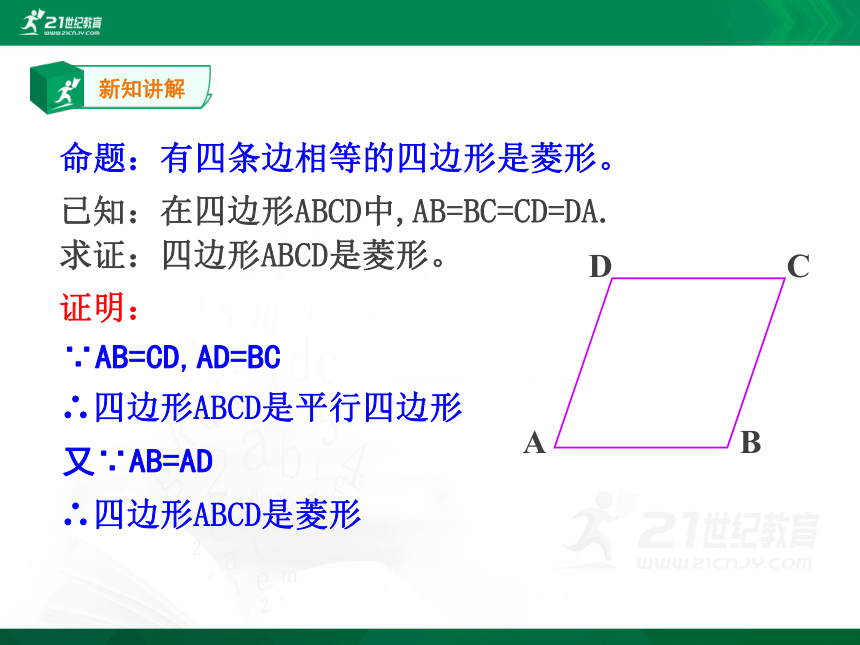
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形。
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD
∴四边形ABCD是菱形
四条边都相等的四边形是菱形.
AB=BC=CD=DA
四边形ABCD是菱形
菱形的判定方法3:
例3 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可。你知道其中的道理吗?
练习:如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
例4 如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.求证:四边形AFCE是菱形。
∵EF垂直平分AC
∴AO=CO, ∠AOE=90°
∴∠FOC=∠AOE=90°
∵四边形ABCD是平行四边形
∴ AD∥BC ∴AE∥FC
∴∠AEO=∠CFO
∴△AEO≌△CFO
证明:
∴OE=OF
又∵AO=CO
∴四边形AFCE是平行四边形
又∵EF⊥AC
∴四边形AFCE是菱形
∟
∟
E
F
例6 如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE。求证:四边形ACEF是菱形。
学到了如何识别菱形
? 今天你学到了什么 ?
菱形的判定方法:
1、一组邻边相等的平行四边形是菱形。
2、对角线互相垂直的平行四边形是菱形。
3、四条边都相等的四边形是菱形。
(对角线互相垂直平分的四边形是菱形)
1.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
2.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
3.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
1.填空:
(1)菱形的两条对角线长分别是3和4,则周长和面积
分别是________、________.
(2)菱形周长为80,一对角线为20,则较小的角的度
数为______,面积为_______.
(3)菱形一边与两条对角线夹角的差是20°,那么菱
形各角的度数分别为________.
(4)已知:菱形的周长为40cm,两条对角线长的比是
3:4。求两对角线长分别是 。
(5)对角线互相平分的四边形是 ;
(6)对角线互相垂直平分的四边形是________;
(7)对角线相等且互相平分的四边形是________;
(8)两组对边分别平行,且对角线 的四边
形是菱形.
2.□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
3.判断下列命题是否正确,并说明理由.
(1)对角线互相平分且邻边相等的四边形是菱形.
(2)两组对边分别平行且一组邻边相等的四边形是菱形.
(3)邻角相等的四边形是菱形.
(4)有一组邻边相等的四边形是菱形.
(5)两组对角分别相等且对角线互相垂直的四边形是菱形.
(6)对角线互相垂直的四边形是菱形.
(7)对角线互相垂直平分的四边形是菱形。
(8)一条对角线平分一个内角的平行四边形是菱形。
(9)对角线互相垂直,且有一组邻边相等的四边形是菱形.
(10)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
4.老师说下列三个图形都是菱形,你相信吗?
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
5.如图,AD是的角平分线,DE∥AC,DF∥AB. 证明:四边形AEDF是菱形。 对于这道,小林是这样证明的。 证明:∵AD平分,∴∠1=∠2,
∵DE∥AC,∴∠2=∠3
∵DF∥AB,∴∠1=∠4
又有AD=AD,∴△AED ≌ △AFD.
∴AE=AF,DE=DF. ∴四边形AEDF是菱形. 老师说小林的解题过程有错误,你能看出来吗? ⑴请你帮小林指出他的错误是什么?(先在解答过程中划出来,再说明他错误的原因) ⑵请你帮小林做出正确的解答。
6.如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF。
7.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.求证:四边形ADCE是菱形。
8.如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.
D
E
F
G
1
2
3
4
5
9.如图:将菱形ABCD沿AC方向平移至A1B1C1D1,A1D1交CD于E,A1B1交BC于F,请问四边形A1FCE是不是菱形?为什么?
作业
1.课本P58页第 2 题
3.练习册 P 25-27 页
2.课本P60页第6、10题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.2.2菱形(2)
怎样判断一个四边形是菱形?
菱形ABCD的性质:
1.具有平行四边形的 一切性质。
2.菱形本身具有的特殊性质: 四条边相等;
两条对角线互相垂直平分, 每一条对角线平分一组对角.
3.菱形的面积等于菱形对角线乘积的一半.
有一组邻边相等的平行四边形叫做菱形。
菱形的定义:
菱形
一组邻边相等
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
根据菱形的定义,可得菱形的判定方法1:
有一组邻边相等的平行四边形叫做菱形.
数学语言:
∵四边形ABCD是平行四边形,且AB=AD
∴四边形ABCD是菱形
例1 如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形.
∴ □AEDF是菱形
证明:∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC
∴∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
练习 如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E.
求证:四边形OCED是菱形.
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
猜想:
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:在□ABCD 中,AC ⊥ BD。求证:□ABCD是菱形。
证明:
∴ □ABCD是菱形
又∵ AC ⊥ BD
∵四边形ABCD是□
∴OA=OC
∴BA=BC
O
菱形的判定方法2:
对角线互相垂直的平行四边形是菱形。
∴四边形ABCD是菱形
(对角线互相垂直平分的四边形是菱形)
∵四边形ABCD是平行四边形,
且AC⊥BD
几何语言:
∴四边形ABCD是菱形.
∴OA=OC=4,OB=OD=3
证明:
又∵AB=5
∴AC⊥BD
∴∠AOB=90°
又∵ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
∴AB2=AO2+BO2
情境:李芳同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
猜想:四边都相等的四边形是菱形 。
A
B
C
D
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形。
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD
∴四边形ABCD是菱形
四条边都相等的四边形是菱形.
AB=BC=CD=DA
四边形ABCD是菱形
菱形的判定方法3:
例3 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可。你知道其中的道理吗?
练习:如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
例4 如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.求证:四边形AFCE是菱形。
∵EF垂直平分AC
∴AO=CO, ∠AOE=90°
∴∠FOC=∠AOE=90°
∵四边形ABCD是平行四边形
∴ AD∥BC ∴AE∥FC
∴∠AEO=∠CFO
∴△AEO≌△CFO
证明:
∴OE=OF
又∵AO=CO
∴四边形AFCE是平行四边形
又∵EF⊥AC
∴四边形AFCE是菱形
∟
∟
E
F
例6 如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE。求证:四边形ACEF是菱形。
学到了如何识别菱形
? 今天你学到了什么 ?
菱形的判定方法:
1、一组邻边相等的平行四边形是菱形。
2、对角线互相垂直的平行四边形是菱形。
3、四条边都相等的四边形是菱形。
(对角线互相垂直平分的四边形是菱形)
1.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
2.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
3.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
1.填空:
(1)菱形的两条对角线长分别是3和4,则周长和面积
分别是________、________.
(2)菱形周长为80,一对角线为20,则较小的角的度
数为______,面积为_______.
(3)菱形一边与两条对角线夹角的差是20°,那么菱
形各角的度数分别为________.
(4)已知:菱形的周长为40cm,两条对角线长的比是
3:4。求两对角线长分别是 。
(5)对角线互相平分的四边形是 ;
(6)对角线互相垂直平分的四边形是________;
(7)对角线相等且互相平分的四边形是________;
(8)两组对边分别平行,且对角线 的四边
形是菱形.
2.□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
3.判断下列命题是否正确,并说明理由.
(1)对角线互相平分且邻边相等的四边形是菱形.
(2)两组对边分别平行且一组邻边相等的四边形是菱形.
(3)邻角相等的四边形是菱形.
(4)有一组邻边相等的四边形是菱形.
(5)两组对角分别相等且对角线互相垂直的四边形是菱形.
(6)对角线互相垂直的四边形是菱形.
(7)对角线互相垂直平分的四边形是菱形。
(8)一条对角线平分一个内角的平行四边形是菱形。
(9)对角线互相垂直,且有一组邻边相等的四边形是菱形.
(10)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
4.老师说下列三个图形都是菱形,你相信吗?
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
5.如图,AD是的角平分线,DE∥AC,DF∥AB. 证明:四边形AEDF是菱形。 对于这道,小林是这样证明的。 证明:∵AD平分,∴∠1=∠2,
∵DE∥AC,∴∠2=∠3
∵DF∥AB,∴∠1=∠4
又有AD=AD,∴△AED ≌ △AFD.
∴AE=AF,DE=DF. ∴四边形AEDF是菱形. 老师说小林的解题过程有错误,你能看出来吗? ⑴请你帮小林指出他的错误是什么?(先在解答过程中划出来,再说明他错误的原因) ⑵请你帮小林做出正确的解答。
6.如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF。
7.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.求证:四边形ADCE是菱形。
8.如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.
D
E
F
G
1
2
3
4
5
9.如图:将菱形ABCD沿AC方向平移至A1B1C1D1,A1D1交CD于E,A1B1交BC于F,请问四边形A1FCE是不是菱形?为什么?
作业
1.课本P58页第 2 题
3.练习册 P 25-27 页
2.课本P60页第6、10题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
