1.2 任意角的三角函数 课件(66张PPT)
文档属性
| 名称 | 1.2 任意角的三角函数 课件(66张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 15:06:32 | ||
图片预览







文档简介
(共66张PPT)
1.2.1 任意角的三角函数
第一课时
本节课以锐角三角函数就是以锐角为自变量,以比值为函数值的函数引导学生把这个定义推广到任意角,通过单位圆和角的终边,探讨任意角的三角函数值的求法,最终得到任意角三角函数的定义.根据角终边所在位置不同,分别探讨各三角函数的定义域以及这三种函数的值在各象限的符号.最后主要是借助有向线段进一步认识三角函数.讲解例题,总结方法,巩固练习.
任意角的三角函数可以有不同的定义方法,而且各种定义都有自己的特点.过去习惯于用角的终边上点的坐标的“比值”来定义,这种定义方法能够表现出从锐角三角函数到任意角的三角函数的推广,有利于引导学生从自己已有认知基础出发学习三角函数,但它对准确把握三角函数的本质有一定的不利影响,“从角的集合到比值的集合”的对应关系与学生熟悉的一般函数概念中的“数集到数集”的对应关系有冲突,而且“比值”需要通过运算才能得到,这与函数值是一个确定的实数也有不同,这些都会影响学生对三角函数概念的理解
(1)掌握任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);
(2)理解任意角的三角函数不同的定义方法
自然界的周期现象
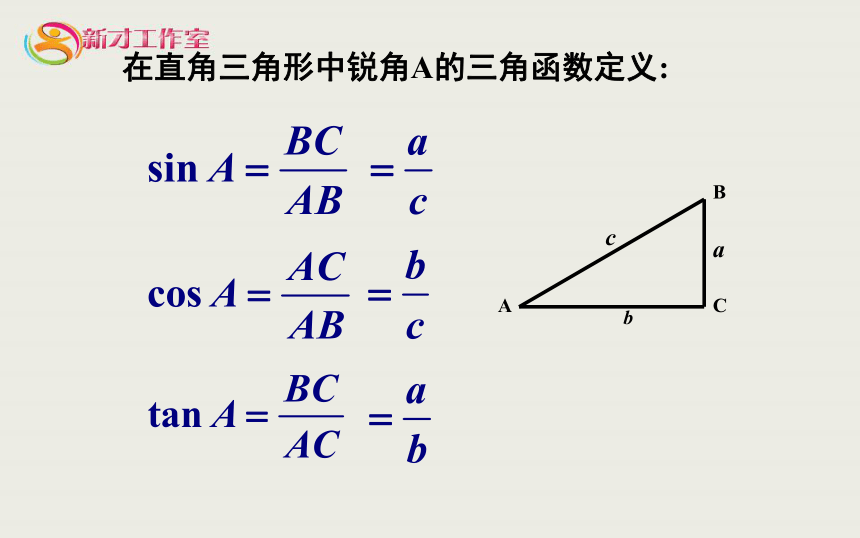
在直角三角形中锐角A的三角函数定义:
A
B
C
a
b
c
上述定义只限于直角三角形中的锐角,
而现在角的定义已经拓广到任意角,如:
O
b
a
M
P
y
x
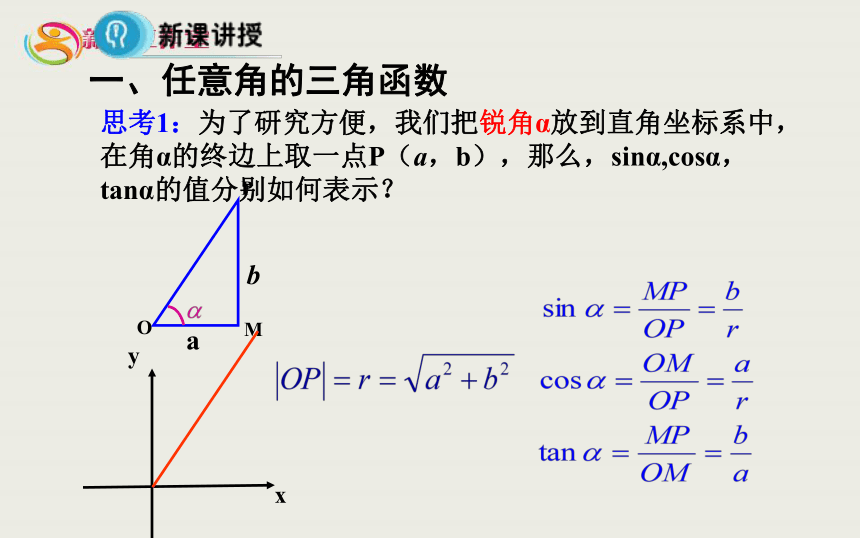
思考1:为了研究方便,我们把锐角α放到直角坐标系中,在角α的终边上取一点P(a,b),那么,sinα,cosα,tanα的值分别如何表示?
一、任意角的三角函数
∽
M
O
y
x
P(a,b)
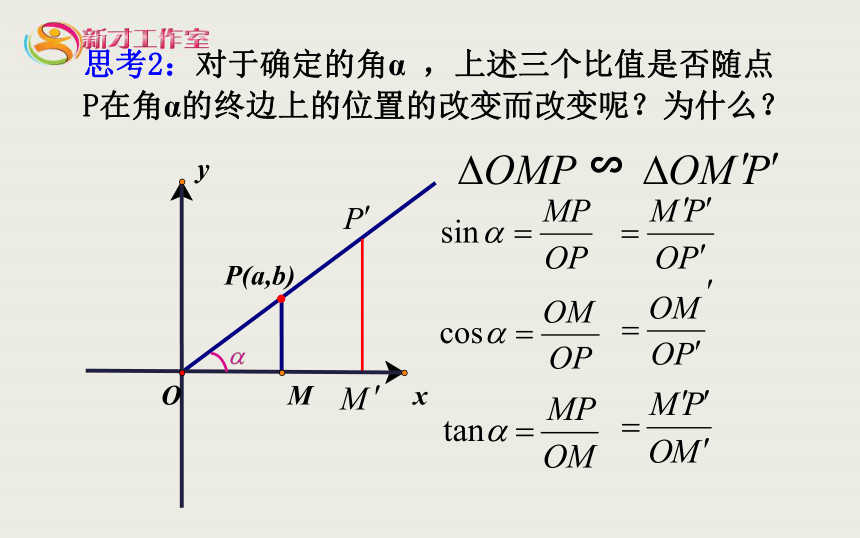
思考2:对于确定的角α ,上述三个比值是否随点P在角α的终边上的位置的改变而改变呢?为什么?
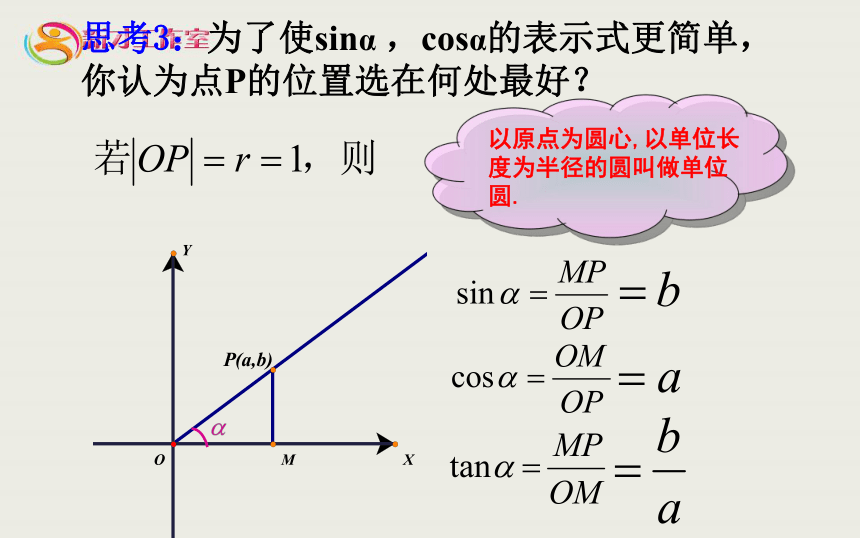
以原点为圆心,以单位长度为半径的圆叫做单位圆.
思考3:为了使sinα ,cosα的表示式更简单,你认为点P的位置选在何处最好?
α的终边
P(x,y)
O
x
y
P(x,y)
α的终边
思考4:设α是一个任意角,它的终边与单位圆交于点P(x,y),为了与当α为锐角时的三角函数保持统一,你认为sinα,cosα,tanα对应的值应分别如何定义?
对应关系 , , 都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数.
思考5:三角函数该如何定义呢?
﹒
注意:无论角a是第几象限角,它的三角函数的定义都是一样。
y
x
O
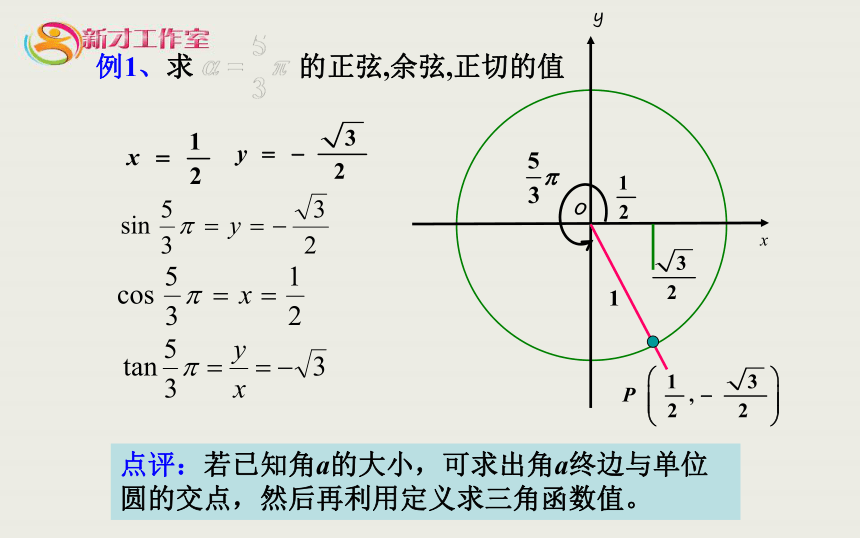
点评:若已知角a的大小,可求出角a终边与单位圆的交点,然后再利用定义求三角函数值。
例1、求 的正弦,余弦,正切的值
O
x
y
P(x,y)
M
分析:可得点
,
故
练习:求角 的正弦、余弦和正切值。
正切函数的定义域是
正、余弦函数的定义域为R,
思考6:在弧度制中,这三个三角函数的定义域分别是什么?
例2 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .
解:由已知可得
设角 的终边与单位圆交于 ,
分别过点 、 作 轴的垂线 、
\
于是,
∽
设角 是一个任意角, 是终边上的
任意一点,点 与原点的距离
那么① 叫做 的正弦,即
② 叫做 的余弦,即
③ 叫做 的正弦,即
任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.
定义推广:
于是,
练习: 已知角 的终边过点 ,
求 的三个三角函数值.
解:由已知可得:
特殊角的三角函数:
不存在
不存在
思考
几何画板演示
的终边
的终边
的终边
的终边
C、D
C
3
1.2.2 同角三角函数基本关系
1.2.1 任意角的三角函数
第一课时
本节课以锐角三角函数就是以锐角为自变量,以比值为函数值的函数引导学生把这个定义推广到任意角,通过单位圆和角的终边,探讨任意角的三角函数值的求法,最终得到任意角三角函数的定义.根据角终边所在位置不同,分别探讨各三角函数的定义域以及这三种函数的值在各象限的符号.最后主要是借助有向线段进一步认识三角函数.讲解例题,总结方法,巩固练习.
任意角的三角函数可以有不同的定义方法,而且各种定义都有自己的特点.过去习惯于用角的终边上点的坐标的“比值”来定义,这种定义方法能够表现出从锐角三角函数到任意角的三角函数的推广,有利于引导学生从自己已有认知基础出发学习三角函数,但它对准确把握三角函数的本质有一定的不利影响,“从角的集合到比值的集合”的对应关系与学生熟悉的一般函数概念中的“数集到数集”的对应关系有冲突,而且“比值”需要通过运算才能得到,这与函数值是一个确定的实数也有不同,这些都会影响学生对三角函数概念的理解
(1)掌握任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);
(2)理解任意角的三角函数不同的定义方法
自然界的周期现象
在直角三角形中锐角A的三角函数定义:
A
B
C
a
b
c
上述定义只限于直角三角形中的锐角,
而现在角的定义已经拓广到任意角,如:
O
b
a
M
P
y
x
思考1:为了研究方便,我们把锐角α放到直角坐标系中,在角α的终边上取一点P(a,b),那么,sinα,cosα,tanα的值分别如何表示?
一、任意角的三角函数
∽
M
O
y
x
P(a,b)
思考2:对于确定的角α ,上述三个比值是否随点P在角α的终边上的位置的改变而改变呢?为什么?
以原点为圆心,以单位长度为半径的圆叫做单位圆.
思考3:为了使sinα ,cosα的表示式更简单,你认为点P的位置选在何处最好?
α的终边
P(x,y)
O
x
y
P(x,y)
α的终边
思考4:设α是一个任意角,它的终边与单位圆交于点P(x,y),为了与当α为锐角时的三角函数保持统一,你认为sinα,cosα,tanα对应的值应分别如何定义?
对应关系 , , 都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数.
思考5:三角函数该如何定义呢?
﹒
注意:无论角a是第几象限角,它的三角函数的定义都是一样。
y
x
O
点评:若已知角a的大小,可求出角a终边与单位圆的交点,然后再利用定义求三角函数值。
例1、求 的正弦,余弦,正切的值
O
x
y
P(x,y)
M
分析:可得点
,
故
练习:求角 的正弦、余弦和正切值。
正切函数的定义域是
正、余弦函数的定义域为R,
思考6:在弧度制中,这三个三角函数的定义域分别是什么?
例2 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .
解:由已知可得
设角 的终边与单位圆交于 ,
分别过点 、 作 轴的垂线 、
\
于是,
∽
设角 是一个任意角, 是终边上的
任意一点,点 与原点的距离
那么① 叫做 的正弦,即
② 叫做 的余弦,即
③ 叫做 的正弦,即
任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.
定义推广:
于是,
练习: 已知角 的终边过点 ,
求 的三个三角函数值.
解:由已知可得:
特殊角的三角函数:
不存在
不存在
思考
几何画板演示
的终边
的终边
的终边
的终边
C、D
C
3
1.2.2 同角三角函数基本关系
