1.5 函数y=Asin(ωx+φ)的图象 课件(39张PPT)
文档属性
| 名称 | 1.5 函数y=Asin(ωx+φ)的图象 课件(39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 00:00:00 | ||
图片预览









文档简介
函数y=Asin(ωx+φ)的图象
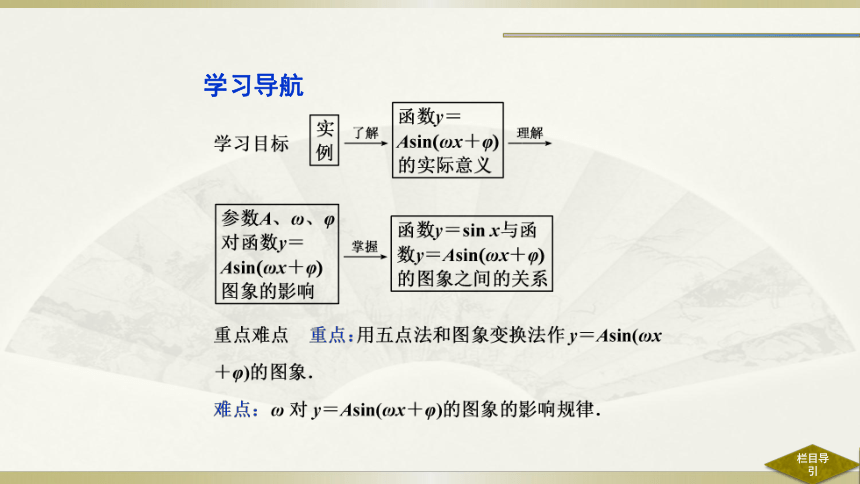
学习导航
新知初探思维启动
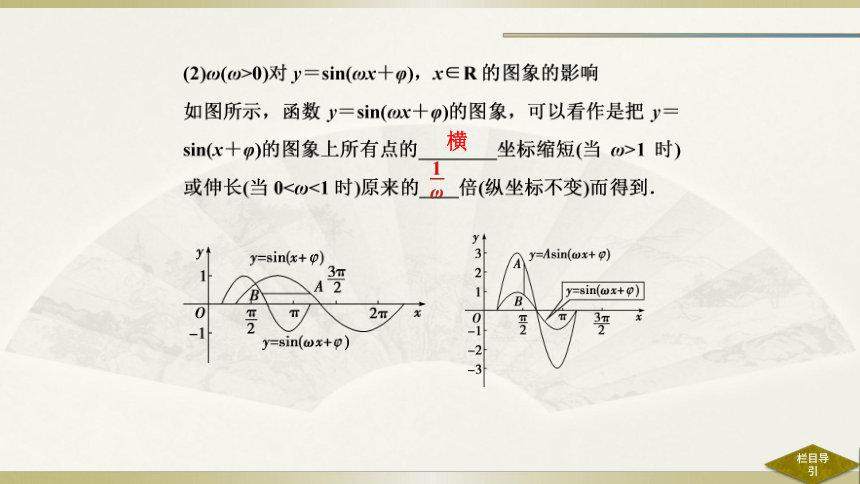
1.A、ω、φ对函数y=Asin(ωx+φ)图象的影响
(1)φ对y=sin(x+φ),x∈R的图象的影响
如图所示,对于函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sin x的图象上所有的点向_____ (当φ>0时)或向____ (当φ<0时)平行移动_____个单位长度得到的.
左
右
|φ|
横
(3)A(A>0)对y=Asin(ωx+φ),x∈R的图象的影响
如图所示,函数y=Asin(ωx+φ)的图象,可以看作是把y=sin(ωx+φ)的图象上的所有点的____坐标伸长(当A>1时)或缩短(当0
纵
A
想一想
用图象“变换法”作图主要有哪几种途径?
提示:有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.
做一做
答案:y=sin 3x
振幅
周期
频率
相位
初相
做一做
答案:6π 2
典题例证技法归纳
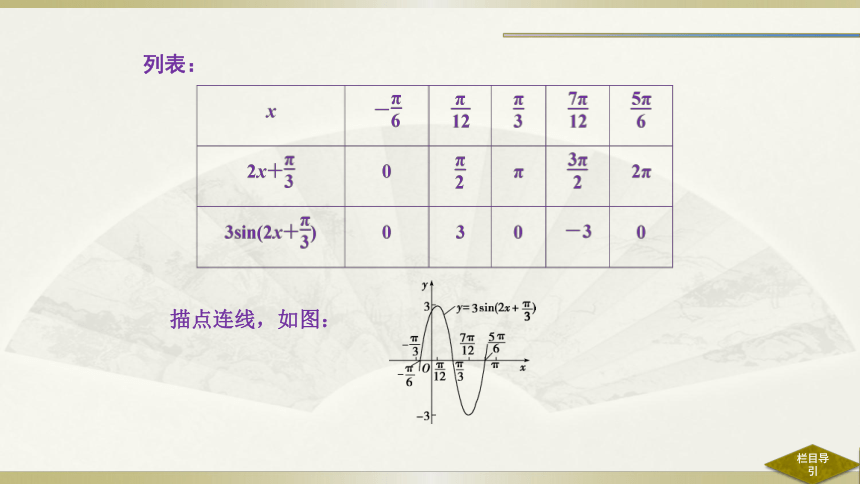
题型一 作函数y=Asin(ωx+φ)的图象
题型探究
例1
列表:
描点连线,如图:
跟踪训练
解:(1)列表:
例2
题型二 求函数y=Asin(ωx+φ)的解析式
【名师点评】 给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法:
(1)第一零点法:如果从图象可直接确定A和ω,则选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”)求得φ.
(2)特殊值法:通过若干特殊点代入函数式,可以求得相关待定系数A,ω,φ.这里需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入列式.
(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y=Asin ωx,再根据图象平移规律确定相关的参数.
跟踪训练
例3
题型三 函数y=Asin(ωx+φ)的性质
【名师点评】 函数y=Asin(ωx+φ)性质的应用
(1)应用的范围:函数的单调性、最值、奇偶性、图象的对称性等方面都有体现和考查.
(2)解决的方法:有关函数y=Asin(ωx+φ)的性质的运用问题,充分利用三角函数的基本性质,要特别注意整体代换的思想的运用.
跟踪训练
3.函数f(x)=Asin(ωx+φ)的图象如图所示,试依图写出:
(1)使f(x)取最小值时的x的取值集合;
(2)图象的对称轴方程;
(3)图象的对称中心;
(4)要使f(x)成为偶函数,应对f(x)的图象作怎样的平移变换?
方法感悟
2.由图象求函数解析式
若已知函数的图象求它对应的解析式,一般要仔细观察图象,从它已表达出的特征,如一个或半个周期,最高点与最低点,与x轴与y轴的交点或其他的特殊点来求.
如果所求函数解析式为y=Asin(ωx+φ),此时最大值与最小值互为相反数.A由图象的最高点或最低点确定.ω由周期T确定,T由相邻的两个最高点或最低点,与x轴或y轴的交点或其他特殊点等确定,φ由已知点的坐标确定,常用五点中的一个.
精彩推荐典例展示
例4
易错警示
平移变换中的误区
【答案】 D
学习导航
新知初探思维启动
1.A、ω、φ对函数y=Asin(ωx+φ)图象的影响
(1)φ对y=sin(x+φ),x∈R的图象的影响
如图所示,对于函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sin x的图象上所有的点向_____ (当φ>0时)或向____ (当φ<0时)平行移动_____个单位长度得到的.
左
右
|φ|
横
(3)A(A>0)对y=Asin(ωx+φ),x∈R的图象的影响
如图所示,函数y=Asin(ωx+φ)的图象,可以看作是把y=sin(ωx+φ)的图象上的所有点的____坐标伸长(当A>1时)或缩短(当0
纵
A
想一想
用图象“变换法”作图主要有哪几种途径?
提示:有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.
做一做
答案:y=sin 3x
振幅
周期
频率
相位
初相
做一做
答案:6π 2
典题例证技法归纳
题型一 作函数y=Asin(ωx+φ)的图象
题型探究
例1
列表:
描点连线,如图:
跟踪训练
解:(1)列表:
例2
题型二 求函数y=Asin(ωx+φ)的解析式
【名师点评】 给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法:
(1)第一零点法:如果从图象可直接确定A和ω,则选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”)求得φ.
(2)特殊值法:通过若干特殊点代入函数式,可以求得相关待定系数A,ω,φ.这里需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入列式.
(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y=Asin ωx,再根据图象平移规律确定相关的参数.
跟踪训练
例3
题型三 函数y=Asin(ωx+φ)的性质
【名师点评】 函数y=Asin(ωx+φ)性质的应用
(1)应用的范围:函数的单调性、最值、奇偶性、图象的对称性等方面都有体现和考查.
(2)解决的方法:有关函数y=Asin(ωx+φ)的性质的运用问题,充分利用三角函数的基本性质,要特别注意整体代换的思想的运用.
跟踪训练
3.函数f(x)=Asin(ωx+φ)的图象如图所示,试依图写出:
(1)使f(x)取最小值时的x的取值集合;
(2)图象的对称轴方程;
(3)图象的对称中心;
(4)要使f(x)成为偶函数,应对f(x)的图象作怎样的平移变换?
方法感悟
2.由图象求函数解析式
若已知函数的图象求它对应的解析式,一般要仔细观察图象,从它已表达出的特征,如一个或半个周期,最高点与最低点,与x轴与y轴的交点或其他的特殊点来求.
如果所求函数解析式为y=Asin(ωx+φ),此时最大值与最小值互为相反数.A由图象的最高点或最低点确定.ω由周期T确定,T由相邻的两个最高点或最低点,与x轴或y轴的交点或其他特殊点等确定,φ由已知点的坐标确定,常用五点中的一个.
精彩推荐典例展示
例4
易错警示
平移变换中的误区
【答案】 D
