八年级下《第七章数据的收集、整理、描述》同步基础练习含答案
文档属性
| 名称 | 八年级下《第七章数据的收集、整理、描述》同步基础练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 22:12:08 | ||
图片预览




文档简介
八年级下册数学(苏科版)-第七章-数据的收集、整理、描述-同步基础练习(含答案)
一、单选题
1. ( 2分 ) 一家鞋店在一段时间内销售了某种女式鞋子38双,其中各种尺码的鞋的销售量如下表:
鞋的尺码(单位:cm)
22.5
23
23.5
24
24.5
销售量(单位:双)
3
6
12
9
8
根据统计的数据,鞋店进货时尺寸码为23cm,23.5cm,24cm的鞋双数合理的比是( )
A.?1:2:4????????????????????????????/B.?2:4:5????????????????????????????/C.?2:4:3????????????????????????????/D.?2:3:4
2. ( 2分 ) 下列调查中,适合用普查的是(??? )
A.?新学期开始,我校调查每一位学生的体重???????????/B.?调查某品牌电视机的使用寿命 C.?调查我市中学生的近视率????????????????????????????????????/D.?调查长江中现有鱼的种类
3. ( 2分 ) 某市从参加数学质量检测的4355名学生中,随机抽取了部分学生的成绩为研究对象,结果如表所示:
/
则被抽取的学生人数是( )
A.?70人??????????????????????????????????/B.?105人??????????????????????????????????/C.?175人??????????????????????????????????/D.?200人
4. ( 2分 ) 如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是(??? )
/
A.?5~10元?????????????????????????????/B.?10~15?????????????????????????????/C.?15~20元?????????????????????????????/D.?20~25元
5. ( 2分 ) 一名同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
/
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.?相声?????????????????????????????????????B.?小品?????????????????????????????????????C.?歌曲?????????????????????????????????????D.?舞蹈
6. ( 2分 ) 在一篇文章中,“的”、“地”、“和”三个字共出现50次,已知“的”和“地”出现的频率之和是0.7,那么“和”字出现的频数是(??? )
A.?14?????????????????????????????????????????B.?15?????????????????????????????????????????C.?16?????????????????????????????????????????D.?17
7. ( 2分 ) 某市体育协会对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68﹣1.70这一小组的频率为0.25,则该组的人数为( )
A.?600人???????????????????????????????????B.?250人???????????????????????????????????C.?60人???????????????????????????????????D.?25人
8. ( 5分 ) 某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在8≤x<32这个范围的频率为(??? )
棉花纤维长度x
频数
0≤x<8
1
8≤x<16
2
16≤x<24
8
24≤x<32
6
32≤x<40
3
A . 0.8?? B . ?? 0.7?? C . ?? 0.4?? D . ?? 0.2
9. ( 2分 ) 频率不可能取到的数为(???? ).
A.?0?????????????????????????????????????????/B.?0.5?????????????????????????????????????????/C.?1?????????????????????????????????????????/D.?1.5
10. ( 2分 ) 下图为某班一次数学成绩的频数分布直方图,则数学成绩在69.5~89.5分范围学生占全体学生的(????) /
A.?47.55%?????????????????????????????????/B.?60%?????????????????????????????????/C.?72.5%?????????????????????????????????/D.?82.5%
二、填空题
11. ( 1分 ) 八年级2班通过投票确定班长,小明同学获得总计40张选票中的30张,得票率超过50%,成为班长,小明得票的频率是________?.
12. ( 1分 ) 一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成________?组.
13. ( 4分 ) 某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图. / 解答下列问题: (1)这次抽样调查的样本容量是________?并补全频数分布直方图; (2)C组学生的频率为________?,在扇形统计图中D组的圆心角是________?度; (3)请你估计该校初三年级体重超过60kg的学生大约有________?名?
14. ( 5分 ) 航模兴趣小组的老师想知道全组学生的年龄情况,于是让大家把自己的年龄写在纸上,下表是全组40名学生的年龄(单位:岁).
14
13
13
15
16
12
14
16
17
13
14
15
12
12
13
14
15
16
15
14
13
12
15
14
17
16
16
13
12
14
14
15
13
16
15
16
17
14
14
13
(1)在这个统计表中,13岁的频数是________?,频率是________?; (2)________?岁的频率最大,这个最大频率是________?; (3)假如老师随机地问一名学生的年龄,你认为老师最可能听到的回答是________?岁 。
15. ( 1分 ) 把64个数据分成8组,从第1组到第4组的频数分别是5,7,11,13,第5组到第7组的频率和是0.125,那么第8组的频数是________。
三、解答题
16. ( 15分 ) 国家规定“中小学生每天在校体育活动时间不低于1小时”,为了解学生参加体育活动的情况。调查了某校八年级甲、乙两班学生每天参加体育锻炼的时间,并将调查结果制成如下的频数分布表和频数分布直方图(数据包括左端点不包括右端点)。 甲班学生每天参加体育活动时间频数分布表
分组(单位:h)
频数
0≤t<0.5
2
0.5≤t<1
10
1≤t<1.5
14
1.5≤t<2
12
2≤t<2.5
2
/ 请你根据图表所提供的信息解答下列问题:
(1)如果每天在校体育活动时间不低于1小时为“达标”,求甲班学生每天在校体育活动时间的达标率。
(2)乙班学生每天参加体育活动时间的中位数落在在哪一组?
(3)请选择一个适当的统计量,对甲、乙两班学生每天参加体育活动的时间进行评价。
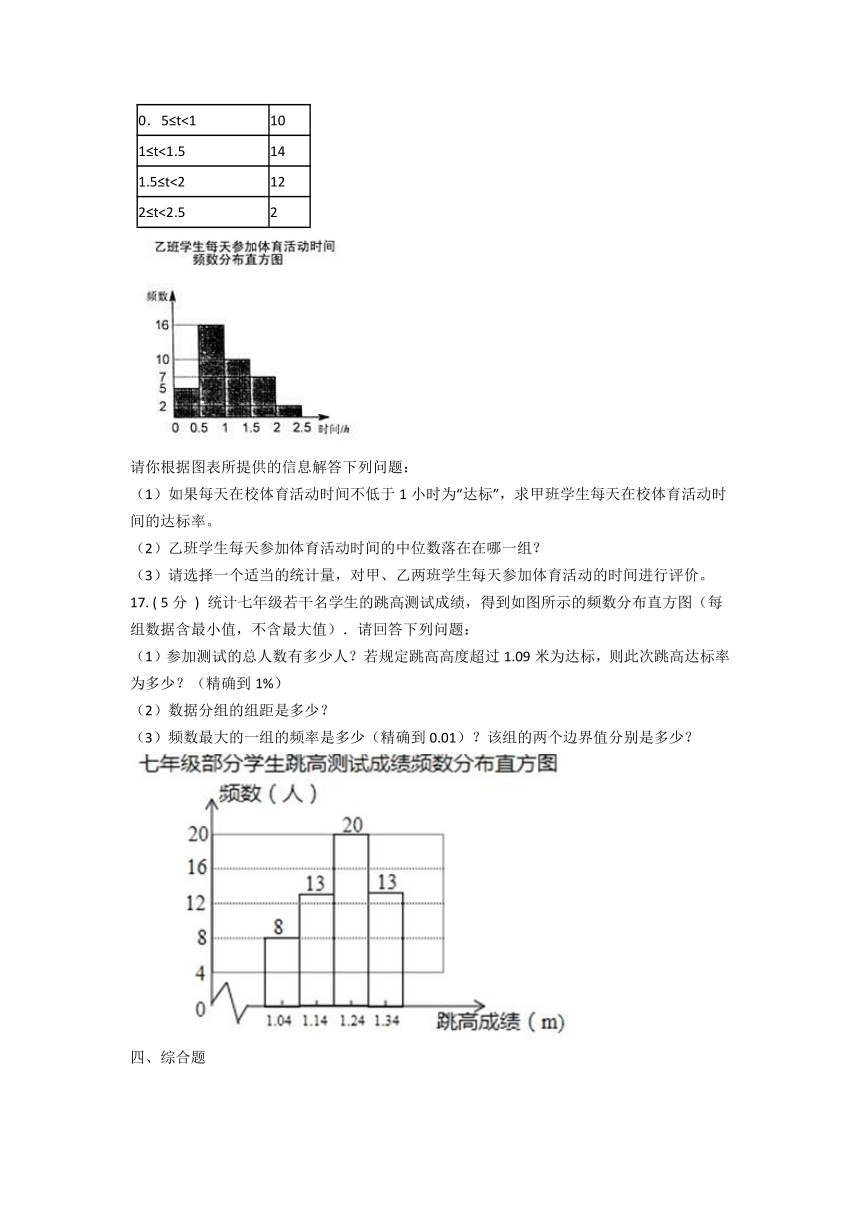
17. ( 5分 ) 统计七年级若干名学生的跳高测试成绩,得到如图所示的频数分布直方图(每组数据含最小值,不含最大值).请回答下列问题: (1)参加测试的总人数有多少人?若规定跳高高度超过1.09米为达标,则此次跳高达标率为多少?(精确到1%) (2)数据分组的组距是多少? (3)频数最大的一组的频率是多少(精确到0.01)?该组的两个边界值分别是多少? ?/
四、综合题
18. ( 13分 ) 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
?60≤x<70
20
0.10
?70≤x<80
30
b
?80≤x<90
a
0.30
?90≤x≤100
80
0.40
请根据所给信息,解答下列问题: /
(1)a=________ , b=________?
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在________?分数段
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
19. ( 15分 ) 北京和南京两城市月降水量统计表(单位:0.1 mm)
月? 份 城? 市
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
北? 京
26
59
90
264
287
707
1 756
1 822
487
188
60
南? 京
288
481
688
866
964
1 592
1 875
1 237
951
599
556
根据上表,回答下列问题:
(1)哪一个城市一年的降水量大?哪一个城市一年的降水量变化幅度大?
(2)两个城市在哪个月的降水量相差最大?差多少?
(3)哪几个月两城市的降水量相差在30 mm以内.
答案部分
一、单选题
1.【答案】 C
【解析】【解答】解:鞋店进货时尺寸码为23cm,23.5cm,24cm的鞋双数合理的比6:12:9=2:4:3,故选C.
【分析】由表中数据可得:23cm,23.5cm,24cm的销售量分别为6、12、9,所以鞋店进货时尺寸码为23cm,23.5cm,24cm的鞋双数合理的比6:12:9=2:4:3.
2.【答案】 A
【解析】【解答】A. 新学期开始,我校调查每一位学生的体重适合普查,故A符合题意;
B. 调查某品牌电视机的使用寿命,调查具有破坏性,适合抽样调查,故B不符合题意;
C. 调查我市中学生的近视率适合抽样调查,故C不符合题意;
D. 调查长江中现有鱼的种类适合抽样调查,故D不符合题意;
故答案为:A.
【分析】普查适用于范围较小,事件较短的一些事件,或者是精确度要求非常高的事件,根据此知识点逐一判断即可。
3.【答案】 C
【解析】【解答】解;∵72~84分数段有35人,所占的百分比是20%,
∴被抽取的学生人数是;35÷20%=175(人);
故选;C.
【分析】先根据统计表得出72~84分数段的人数,再根据所占的百分比是20%,列出算式计算即可.
4.【答案】C
【解析】【解答】解:根据图形所给出的数据可得:
15-20元的有20人,人数最多,
则捐款人数最多的一组是15-20元;
故答案为:C.
【分析】根据图形所给出的数据可得15-20元的有20人,人数最多,得到捐款人数最多的一组是15-20元.
5.【答案】 D
【解析】【解答】解:由统计表可得:
A、相声划记应为5人,则百分数应为/×100%=10%,故错误;
B、小品划记应为16人,则百分数应为/×100%=32%,故错误;
C、歌曲划记为应10人,则百分数则百分数应为/×100%=20%,故错误;
D、舞蹈的划记为6人是正确的,百分数为/×100%=12%,百分数也正确,故正确.
故选D.
【分析】此题只需根据划记的人数除以总人数,正确计算百分比,即可进行分析判断.
6.【答案】 B
【解析】【解答】解:由题可得,“和”字出现的频率是1﹣0.7=0.3,
∴“和”字出现的频数是50×0.3=15;
故答案为:B.
【分析】先求出“和”字出现的频率,再乘以50,就可求出“和”字出现的频数。
7.【答案】 A
【解析】【解答】解:由题意,该组的人数为:2400×0.25=600(人).
故选A.
【分析】根据频数=频率×数据总和进行解答即可.
8.【答案】A
【解析】【解答】解:在8≤x<32这个范围的频数是:2+8+6=16, 则在8≤x<32这个范围的频率是: /=0.8. 故答案为:A . 【分析】根据题意得到在8≤x<32这个范围的频数是2+8+6,求出在这个范围的频率是16÷20.
9.【答案】 D
【解析】【解答】解:频率不能超过1,故不能取到大于1的数,故答案为:D。
【分析】频率不能超过1,故不能取到大于1的数.
10.【答案】 B
【解析】【分析】由图像可知在69.5~89.5分范围人数为10+14=24(人) 【解答】全部人数为2+9+5+24=40(人) 故则数学成绩在69.5~89.5分范围学生占全体学生的/;
选B。 【点评】本题难度较低,主要考查学生对频数分布直方图知识点的掌握,读懂直方图中横纵轴读数与对应含义为解题关键。
二、填空题
11.【答案】0.75
【解析】【解答】解:∵小明同学获得总计40张选票中的30张, ∴频数为30,数据总数为40, ∴频率= 频数/数据总和=/=0.75. 故答案为:0.75. 【分析】根据频数与频率的关系:频率=频数/数据总和,解答即可.
12.【答案】10
【解析】【解答】解:143﹣50=93, 93÷10=9.3, 所以应该分成10组. 故答案为:10. 【分析】求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
13.【答案】50;0.32;72;360
【解析】【解答】解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12, 补全频数分布直方图,如图: / (2)C组学生的频率是0.32;D组的圆心角=/; (3)样本中体重超过60kg的学生是10+8=18人, 该校初三年级体重超过60kg的学生=/人, 故答案为:(1)50;(2)0.32;72. 【分析】(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可; (2)由图表得出C组学生的频率,并计算出D组的圆心角即可; (3)根据样本估计总体即可.
14.【答案】8;0.2;14;0.25;14
【解析】【解答】解:(1)13岁出现的次数为:8次, 即频数为8,频率为:/=0.2, 故答案为:8,0.2; (2)由图可得,12岁出现的频数为:5,14岁出现的频数为:10,15岁出现的频数为:7,16岁出现的频数为:7,17岁出现的频数为:3, 14岁出现的频数最大,即14岁的频率最大,频率为:/=0.25, 故答案为:14,0.25; (3)因为14岁的频率最大, 所以老师最可能听到的回答为:14岁. 【分析】(1)根据频数和频率的定义求解; (2)找出出现次数最多的年龄,求出其频率; (3)做可能听到的回答就是出现频率最大的年龄.
15.【答案】4
【解析】【解答】第5组到第7组的频率是0.125,且容量是64,那么第5组到第7组的频数是64×0.125=8,那么第8组的频数是64-(5+7+11+13+8×3)=4
三、解答题
16.【答案】(1)解: /,答:达标率为70%。 (2)解:5+16+10+7+2=40(人),则中位数是第20和21个数的平均数,而5+16=21,故中位数落在0.5≤x<1。 (3)解:选中位数(或众数),甲班的中位数在1≤t<1.5上,乙班的中位数落在0.5≤x<1,即甲班的中位数比乙班的中位数大,∴甲班学生每天参加体育活动的时间比乙班的多。
【解析】【分析】(1)求出甲班总人数,以及不低于1小时的人数,用不低于1小时的人数除以总人数×100%就是达标率;(2)从频数分布直方图得乙班每组的人数,则可得乙班总人数为40,则中位数为第20和21个的中平均数;(3)此题适合选取中位数、众数进行作比较,哪个数更大,说明哪个班好于另外一个班。
17.【答案】解:(1)总人数是:8+13+20+13=54(人), 此次跳高达标率是: /%≈85.2%; (2)组距是1.04﹣1.04=0.1(m). (3)最大一组的频率是/≈0.37. 该组的两个边界值是:1.19m和1.29m.
【解析】【分析】(1)求得各组的频数的和即可求解; ???????????? (2)利用横轴上相邻两个数值的差就是组距; ???????????? (3)根据(2)的计算结果即可直接求得.
四、综合题
18.【答案】(1)60;0.15 (2)补全频数分布直方图,如下: / (3)80≤x<90 (4)3000×0.40=1200(人). 即该校参加这次比赛的3000名学生中成绩“优”等的大约有1200人.
【解析】【解答】解:(1)样本容量是:10÷0.05=200, a=200×0.30=60,b=30÷200=0.15; (2)补全频数分布直方图,如下: / (3)一共有200个数据,按照从小到大的顺序排列后,第100个与第101个数据都落在第四个分数段, 所以这次比赛成绩的中位数会落在80≤x<90分数段; (4)3000×0.40=1200(人). 即该校参加这次比赛的3000名学生中成绩“优”等的大约有1200人. 故答案为60,0.15;80≤x<90;1200. 【分析】(1)根据第一组的频数是10,频率是0.05,求得数据总数,再用数据总数乘以第四组频率可得a的值,用第三组频数除以数据总数可得b的值; (2)根据(1)的计算结果即可补全频数分布直方图; (3)根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数; (4)利用总数3000乘以“优”等学生的所占的频率即可.
19.【答案】(1)解:北京一年的降水量为579.9 mm,南京一年的降水量为1 041. 9 mm,所以南京一年的降水量大.北京降水量的波动范围从2.6 mm到182.2 mm.南京降水量的波动范围从28.8 mm到187.5 mm,因此北京一年的降水量变化幅度大. (2)解:比较每个月两个城市降水量差,可得6月份两个城市的降水量相差最大, 为159.2—70.7=88.5(mm) (3)解:其中1月、7月两城市的降水量相差在30 mm以内
【解析】【分析】(1)观察表中的数据分析比较即可。 (2)把两个城市每个月的降水量求差比较,即可得出结果。 (3)分半把每个月的降水量求差比较,即可得出对应的月份。
一、单选题
1. ( 2分 ) 一家鞋店在一段时间内销售了某种女式鞋子38双,其中各种尺码的鞋的销售量如下表:
鞋的尺码(单位:cm)
22.5
23
23.5
24
24.5
销售量(单位:双)
3
6
12
9
8
根据统计的数据,鞋店进货时尺寸码为23cm,23.5cm,24cm的鞋双数合理的比是( )
A.?1:2:4????????????????????????????/B.?2:4:5????????????????????????????/C.?2:4:3????????????????????????????/D.?2:3:4
2. ( 2分 ) 下列调查中,适合用普查的是(??? )
A.?新学期开始,我校调查每一位学生的体重???????????/B.?调查某品牌电视机的使用寿命 C.?调查我市中学生的近视率????????????????????????????????????/D.?调查长江中现有鱼的种类
3. ( 2分 ) 某市从参加数学质量检测的4355名学生中,随机抽取了部分学生的成绩为研究对象,结果如表所示:
/
则被抽取的学生人数是( )
A.?70人??????????????????????????????????/B.?105人??????????????????????????????????/C.?175人??????????????????????????????????/D.?200人
4. ( 2分 ) 如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是(??? )
/
A.?5~10元?????????????????????????????/B.?10~15?????????????????????????????/C.?15~20元?????????????????????????????/D.?20~25元
5. ( 2分 ) 一名同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
/
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.?相声?????????????????????????????????????B.?小品?????????????????????????????????????C.?歌曲?????????????????????????????????????D.?舞蹈
6. ( 2分 ) 在一篇文章中,“的”、“地”、“和”三个字共出现50次,已知“的”和“地”出现的频率之和是0.7,那么“和”字出现的频数是(??? )
A.?14?????????????????????????????????????????B.?15?????????????????????????????????????????C.?16?????????????????????????????????????????D.?17
7. ( 2分 ) 某市体育协会对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68﹣1.70这一小组的频率为0.25,则该组的人数为( )
A.?600人???????????????????????????????????B.?250人???????????????????????????????????C.?60人???????????????????????????????????D.?25人
8. ( 5分 ) 某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在8≤x<32这个范围的频率为(??? )
棉花纤维长度x
频数
0≤x<8
1
8≤x<16
2
16≤x<24
8
24≤x<32
6
32≤x<40
3
A . 0.8?? B . ?? 0.7?? C . ?? 0.4?? D . ?? 0.2
9. ( 2分 ) 频率不可能取到的数为(???? ).
A.?0?????????????????????????????????????????/B.?0.5?????????????????????????????????????????/C.?1?????????????????????????????????????????/D.?1.5
10. ( 2分 ) 下图为某班一次数学成绩的频数分布直方图,则数学成绩在69.5~89.5分范围学生占全体学生的(????) /
A.?47.55%?????????????????????????????????/B.?60%?????????????????????????????????/C.?72.5%?????????????????????????????????/D.?82.5%
二、填空题
11. ( 1分 ) 八年级2班通过投票确定班长,小明同学获得总计40张选票中的30张,得票率超过50%,成为班长,小明得票的频率是________?.
12. ( 1分 ) 一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成________?组.
13. ( 4分 ) 某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图. / 解答下列问题: (1)这次抽样调查的样本容量是________?并补全频数分布直方图; (2)C组学生的频率为________?,在扇形统计图中D组的圆心角是________?度; (3)请你估计该校初三年级体重超过60kg的学生大约有________?名?
14. ( 5分 ) 航模兴趣小组的老师想知道全组学生的年龄情况,于是让大家把自己的年龄写在纸上,下表是全组40名学生的年龄(单位:岁).
14
13
13
15
16
12
14
16
17
13
14
15
12
12
13
14
15
16
15
14
13
12
15
14
17
16
16
13
12
14
14
15
13
16
15
16
17
14
14
13
(1)在这个统计表中,13岁的频数是________?,频率是________?; (2)________?岁的频率最大,这个最大频率是________?; (3)假如老师随机地问一名学生的年龄,你认为老师最可能听到的回答是________?岁 。
15. ( 1分 ) 把64个数据分成8组,从第1组到第4组的频数分别是5,7,11,13,第5组到第7组的频率和是0.125,那么第8组的频数是________。
三、解答题
16. ( 15分 ) 国家规定“中小学生每天在校体育活动时间不低于1小时”,为了解学生参加体育活动的情况。调查了某校八年级甲、乙两班学生每天参加体育锻炼的时间,并将调查结果制成如下的频数分布表和频数分布直方图(数据包括左端点不包括右端点)。 甲班学生每天参加体育活动时间频数分布表
分组(单位:h)
频数
0≤t<0.5
2
0.5≤t<1
10
1≤t<1.5
14
1.5≤t<2
12
2≤t<2.5
2
/ 请你根据图表所提供的信息解答下列问题:
(1)如果每天在校体育活动时间不低于1小时为“达标”,求甲班学生每天在校体育活动时间的达标率。
(2)乙班学生每天参加体育活动时间的中位数落在在哪一组?
(3)请选择一个适当的统计量,对甲、乙两班学生每天参加体育活动的时间进行评价。
17. ( 5分 ) 统计七年级若干名学生的跳高测试成绩,得到如图所示的频数分布直方图(每组数据含最小值,不含最大值).请回答下列问题: (1)参加测试的总人数有多少人?若规定跳高高度超过1.09米为达标,则此次跳高达标率为多少?(精确到1%) (2)数据分组的组距是多少? (3)频数最大的一组的频率是多少(精确到0.01)?该组的两个边界值分别是多少? ?/
四、综合题
18. ( 13分 ) 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
?60≤x<70
20
0.10
?70≤x<80
30
b
?80≤x<90
a
0.30
?90≤x≤100
80
0.40
请根据所给信息,解答下列问题: /
(1)a=________ , b=________?
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在________?分数段
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
19. ( 15分 ) 北京和南京两城市月降水量统计表(单位:0.1 mm)
月? 份 城? 市
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
北? 京
26
59
90
264
287
707
1 756
1 822
487
188
60
南? 京
288
481
688
866
964
1 592
1 875
1 237
951
599
556
根据上表,回答下列问题:
(1)哪一个城市一年的降水量大?哪一个城市一年的降水量变化幅度大?
(2)两个城市在哪个月的降水量相差最大?差多少?
(3)哪几个月两城市的降水量相差在30 mm以内.
答案部分
一、单选题
1.【答案】 C
【解析】【解答】解:鞋店进货时尺寸码为23cm,23.5cm,24cm的鞋双数合理的比6:12:9=2:4:3,故选C.
【分析】由表中数据可得:23cm,23.5cm,24cm的销售量分别为6、12、9,所以鞋店进货时尺寸码为23cm,23.5cm,24cm的鞋双数合理的比6:12:9=2:4:3.
2.【答案】 A
【解析】【解答】A. 新学期开始,我校调查每一位学生的体重适合普查,故A符合题意;
B. 调查某品牌电视机的使用寿命,调查具有破坏性,适合抽样调查,故B不符合题意;
C. 调查我市中学生的近视率适合抽样调查,故C不符合题意;
D. 调查长江中现有鱼的种类适合抽样调查,故D不符合题意;
故答案为:A.
【分析】普查适用于范围较小,事件较短的一些事件,或者是精确度要求非常高的事件,根据此知识点逐一判断即可。
3.【答案】 C
【解析】【解答】解;∵72~84分数段有35人,所占的百分比是20%,
∴被抽取的学生人数是;35÷20%=175(人);
故选;C.
【分析】先根据统计表得出72~84分数段的人数,再根据所占的百分比是20%,列出算式计算即可.
4.【答案】C
【解析】【解答】解:根据图形所给出的数据可得:
15-20元的有20人,人数最多,
则捐款人数最多的一组是15-20元;
故答案为:C.
【分析】根据图形所给出的数据可得15-20元的有20人,人数最多,得到捐款人数最多的一组是15-20元.
5.【答案】 D
【解析】【解答】解:由统计表可得:
A、相声划记应为5人,则百分数应为/×100%=10%,故错误;
B、小品划记应为16人,则百分数应为/×100%=32%,故错误;
C、歌曲划记为应10人,则百分数则百分数应为/×100%=20%,故错误;
D、舞蹈的划记为6人是正确的,百分数为/×100%=12%,百分数也正确,故正确.
故选D.
【分析】此题只需根据划记的人数除以总人数,正确计算百分比,即可进行分析判断.
6.【答案】 B
【解析】【解答】解:由题可得,“和”字出现的频率是1﹣0.7=0.3,
∴“和”字出现的频数是50×0.3=15;
故答案为:B.
【分析】先求出“和”字出现的频率,再乘以50,就可求出“和”字出现的频数。
7.【答案】 A
【解析】【解答】解:由题意,该组的人数为:2400×0.25=600(人).
故选A.
【分析】根据频数=频率×数据总和进行解答即可.
8.【答案】A
【解析】【解答】解:在8≤x<32这个范围的频数是:2+8+6=16, 则在8≤x<32这个范围的频率是: /=0.8. 故答案为:A . 【分析】根据题意得到在8≤x<32这个范围的频数是2+8+6,求出在这个范围的频率是16÷20.
9.【答案】 D
【解析】【解答】解:频率不能超过1,故不能取到大于1的数,故答案为:D。
【分析】频率不能超过1,故不能取到大于1的数.
10.【答案】 B
【解析】【分析】由图像可知在69.5~89.5分范围人数为10+14=24(人) 【解答】全部人数为2+9+5+24=40(人) 故则数学成绩在69.5~89.5分范围学生占全体学生的/;
选B。 【点评】本题难度较低,主要考查学生对频数分布直方图知识点的掌握,读懂直方图中横纵轴读数与对应含义为解题关键。
二、填空题
11.【答案】0.75
【解析】【解答】解:∵小明同学获得总计40张选票中的30张, ∴频数为30,数据总数为40, ∴频率= 频数/数据总和=/=0.75. 故答案为:0.75. 【分析】根据频数与频率的关系:频率=频数/数据总和,解答即可.
12.【答案】10
【解析】【解答】解:143﹣50=93, 93÷10=9.3, 所以应该分成10组. 故答案为:10. 【分析】求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
13.【答案】50;0.32;72;360
【解析】【解答】解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12, 补全频数分布直方图,如图: / (2)C组学生的频率是0.32;D组的圆心角=/; (3)样本中体重超过60kg的学生是10+8=18人, 该校初三年级体重超过60kg的学生=/人, 故答案为:(1)50;(2)0.32;72. 【分析】(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可; (2)由图表得出C组学生的频率,并计算出D组的圆心角即可; (3)根据样本估计总体即可.
14.【答案】8;0.2;14;0.25;14
【解析】【解答】解:(1)13岁出现的次数为:8次, 即频数为8,频率为:/=0.2, 故答案为:8,0.2; (2)由图可得,12岁出现的频数为:5,14岁出现的频数为:10,15岁出现的频数为:7,16岁出现的频数为:7,17岁出现的频数为:3, 14岁出现的频数最大,即14岁的频率最大,频率为:/=0.25, 故答案为:14,0.25; (3)因为14岁的频率最大, 所以老师最可能听到的回答为:14岁. 【分析】(1)根据频数和频率的定义求解; (2)找出出现次数最多的年龄,求出其频率; (3)做可能听到的回答就是出现频率最大的年龄.
15.【答案】4
【解析】【解答】第5组到第7组的频率是0.125,且容量是64,那么第5组到第7组的频数是64×0.125=8,那么第8组的频数是64-(5+7+11+13+8×3)=4
三、解答题
16.【答案】(1)解: /,答:达标率为70%。 (2)解:5+16+10+7+2=40(人),则中位数是第20和21个数的平均数,而5+16=21,故中位数落在0.5≤x<1。 (3)解:选中位数(或众数),甲班的中位数在1≤t<1.5上,乙班的中位数落在0.5≤x<1,即甲班的中位数比乙班的中位数大,∴甲班学生每天参加体育活动的时间比乙班的多。
【解析】【分析】(1)求出甲班总人数,以及不低于1小时的人数,用不低于1小时的人数除以总人数×100%就是达标率;(2)从频数分布直方图得乙班每组的人数,则可得乙班总人数为40,则中位数为第20和21个的中平均数;(3)此题适合选取中位数、众数进行作比较,哪个数更大,说明哪个班好于另外一个班。
17.【答案】解:(1)总人数是:8+13+20+13=54(人), 此次跳高达标率是: /%≈85.2%; (2)组距是1.04﹣1.04=0.1(m). (3)最大一组的频率是/≈0.37. 该组的两个边界值是:1.19m和1.29m.
【解析】【分析】(1)求得各组的频数的和即可求解; ???????????? (2)利用横轴上相邻两个数值的差就是组距; ???????????? (3)根据(2)的计算结果即可直接求得.
四、综合题
18.【答案】(1)60;0.15 (2)补全频数分布直方图,如下: / (3)80≤x<90 (4)3000×0.40=1200(人). 即该校参加这次比赛的3000名学生中成绩“优”等的大约有1200人.
【解析】【解答】解:(1)样本容量是:10÷0.05=200, a=200×0.30=60,b=30÷200=0.15; (2)补全频数分布直方图,如下: / (3)一共有200个数据,按照从小到大的顺序排列后,第100个与第101个数据都落在第四个分数段, 所以这次比赛成绩的中位数会落在80≤x<90分数段; (4)3000×0.40=1200(人). 即该校参加这次比赛的3000名学生中成绩“优”等的大约有1200人. 故答案为60,0.15;80≤x<90;1200. 【分析】(1)根据第一组的频数是10,频率是0.05,求得数据总数,再用数据总数乘以第四组频率可得a的值,用第三组频数除以数据总数可得b的值; (2)根据(1)的计算结果即可补全频数分布直方图; (3)根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数; (4)利用总数3000乘以“优”等学生的所占的频率即可.
19.【答案】(1)解:北京一年的降水量为579.9 mm,南京一年的降水量为1 041. 9 mm,所以南京一年的降水量大.北京降水量的波动范围从2.6 mm到182.2 mm.南京降水量的波动范围从28.8 mm到187.5 mm,因此北京一年的降水量变化幅度大. (2)解:比较每个月两个城市降水量差,可得6月份两个城市的降水量相差最大, 为159.2—70.7=88.5(mm) (3)解:其中1月、7月两城市的降水量相差在30 mm以内
【解析】【分析】(1)观察表中的数据分析比较即可。 (2)把两个城市每个月的降水量求差比较,即可得出结果。 (3)分半把每个月的降水量求差比较,即可得出对应的月份。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
