1.1 正玄定理和余弦定理 课件(61张PPT)
文档属性
| 名称 | 1.1 正玄定理和余弦定理 课件(61张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-12 16:01:59 | ||
图片预览










文档简介
正弦定理、余弦定理
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
1.正弦定理、余弦定理
知识梳理
定理 正弦定理 余弦定理
内容 = = =2R a2= ;
b2= ;
c2=_______________
b2+c2-2bccos A
c2+a2-2cacos B
a2+b2-2abcos C
变形 (1)a=2Rsin A,b= ,c= ;
(2)sin A= ,sin B= ,sin C= ;
(3)a∶b∶c= ;
(4)asin B=bsin A,
bsin C=csin B,
asin C=csin A cos A= ;
cos B= ;
cos C=____________
2Rsin B
2Rsin C
sin A∶sin B∶sin C
3.三角形常用面积公式
(1)S= a·ha(ha表示边a上的高);
(2)S= absin C= = ;
(3)S= r(a+b+c)(r为三角形内切圆半径).
acsin B
bcsin A
1.三角形内角和定理
在△ABC中,A+B+C=π;
知识拓展
2.三角形中的三角函数关系
(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)三角形中三边之比等于相应的三个内角之比.( )
(2)在△ABC中,若sin A>sin B,则A>B.( )
(3)在△ABC的六个元素中,已知任意三个元素可求其他元素.( )
(4)当b2+c2-a2>0时,三角形ABC为锐角三角形.( )
(5)在△ABC中, .( )
(6)在三角形中,已知两边和一角就能求三角形的面积.( )
思考辨析
×
√
×
×
√
√
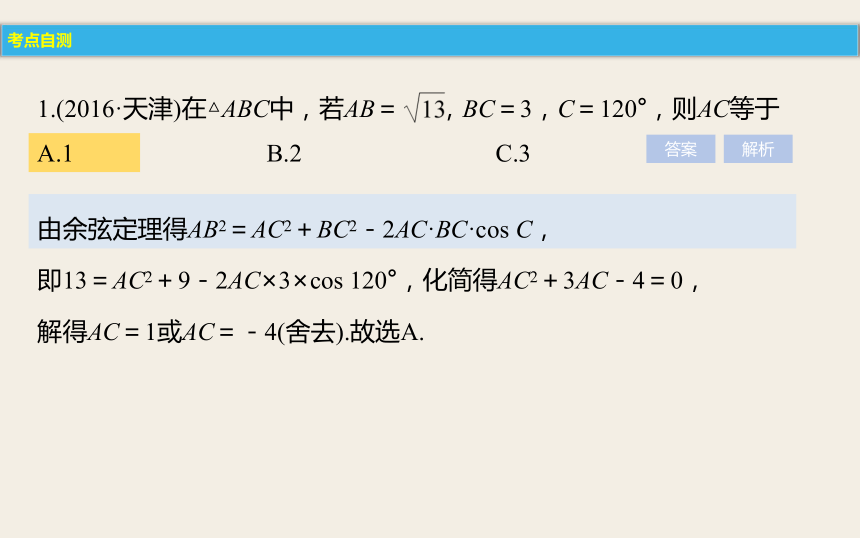
1.(2016·天津)在△ABC中,若AB= ,BC=3,C=120°,则AC等于
A.1 B.2 C.3 D.4
考点自测
答案
解析
由余弦定理得AB2=AC2+BC2-2AC·BC·cos C,
即13=AC2+9-2AC×3×cos 120°,化简得AC2+3AC-4=0,
解得AC=1或AC=-4(舍去).故选A.
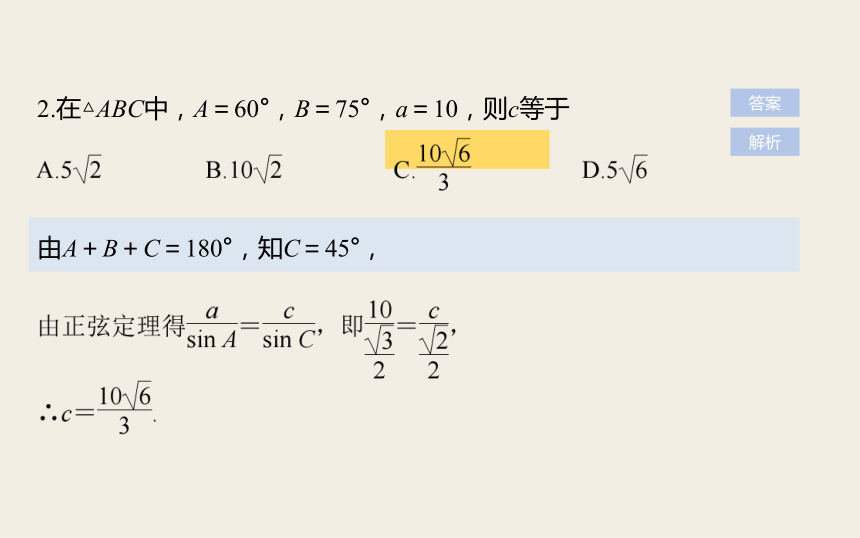
2.在△ABC中,A=60°,B=75°,a=10,则c等于
答案
解析
由A+B+C=180°,知C=45°,
3.在△ABC中,角A,B,C所对的边分别为a,b,c,若
C.锐角三角形 D.等边三角形
答案
解析
因为B∈(0,π),所以sin B>0,所以sin C
4.(2016·辽宁五校联考)设△ABC的内角A,B,C所对边长分别为a,b,c,若b+c=2a,3sin A=5sin B,则角C= .
答案
解析
因为3sin A=5sin B,所以由正弦定理可得3a=5b.
令a=5,b=3,c=7,
则由余弦定理c2=a2+b2-2abcos C,
得49=25+9-2×3×5cos C,
答案
解析
题型分类 深度剖析
题型一 利用正弦定理、余弦定理解三角形
答案
解析
1
①证明:sin Asin B=sin C;
证明
则a=ksin A,b=ksin B,c=ksin C,
sin Asin B=sin Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π-C)=sin C.
所以sin Asin B=sin C.
解答
由(1)知,sin Asin B=sin Acos B+cos Asin B,
思维升华
应用正弦、余弦定理的解题技巧
(3)已知两边和夹角或已知三边可利用余弦定理求解.
(4)灵活利用式子的特点转化:如出现a2+b2-c2=λab形式用余弦定理,等式两边是关于边或角的正弦的齐次式用正弦定理.
答案
解析
(边化角)
(2)在△ABC中,内角A,B,C的对边长分别为a,b,c,已知a2-c2=b,且sin(A-C)=2cos Asin C,则b等于
A.6 B.4 C.2 D.1
答案
解析
(角化边)
由题意,得sin Acos C-cos Asin C=2cos Asin C,
即sin Acos C=3cos Asin C,
由正弦、余弦定理,得
整理得2(a2-c2)=b2, ①
又a2-c2=b, ②
联立①②得b=2,故选C.
题型二 和三角形面积有关的问题
例2 (2016·浙江)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2acos B.
(1)证明:A=2B;
证明
由正弦定理得sin B+sin C=2sin Acos B,
故2sin Acos B=sin B+sin(A+B)=sin B+sin Acos B+cos Asin B,
于是sin B=sin(A-B).
又A,B∈(0,π),故0<A-B<π,
所以B=π-(A-B)或B=A-B,
因此A=π(舍去)或A=2B,所以A=2B.
解答
由sin B≠0,得sin C=cos B.
思维升华
(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化.
跟踪训练2 在△ABC中,内角A,B,C所对的边分别是a,b,c.若c2=(a-b)2+6,C= ,则△ABC的面积是
答案
解析
∵c2=(a-b)2+6,
∴c2=a2+b2-2ab+6. ①
由①②得-ab+6=0,即ab=6.
题型三 正弦定理、余弦定理的简单应用
命题点1 判断三角形的形状
例3 (1)在△ABC中,角A,B,C所对的边分别为a,b,c,若
C.锐角三角形 D.等边三角形
答案
解析
即sin(A+B)
即B为钝角,所以△ABC为钝角三角形.
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+
ccos B=asin A,则△ABC的形状为
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
答案
解析
由正弦定理得sin Bcos C+sin Ccos B=sin2A,
∴sin(B+C)=sin2A,
即sin(π-A)=sin2A,sin A=sin2A.
∵A∈(0,π),∴sin A>0,∴sin A=1,
即A= ,∴△ABC为直角三角形.
引申探究
1.例3(2)中,若将条件变为2sin Acos B=sin C,判断△ABC的形状.
解答
∵2sin Acos B=sin C=sin(A+B),
∴2sin Acos B=sin Acos B+cos Bsin A,
∴sin(A-B)=0,
又A,B为△ABC的内角.
∴A=B,∴△ABC为等腰三角形.
2.例3(2)中,若将条件变为a2+b2-c2=ab,且2cos Asin B=sin C,判断△ABC的形状.
解答
又由2cos Asin B=sin C得sin(B-A)=0,∴A=B,
故△ABC为等边三角形.
命题点2 求解几何计算问题
解答
例4 (2015·课标全国Ⅱ)如图,在△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍.
因为S△ABD=2S△ADC,∠BAD=∠CAD,
所以AB=2AC.
(2)若AD=1,DC= ,求BD和AC的长.
解答
在△ABD和△ADC中,由余弦定理,知
AB2=AD2+BD2-2AD·BDcos∠ADB,
AC2=AD2+DC2-2AD·DCcos∠ADC.
故AB2+2AC2=3AD2+BD2+2DC2=6,
又由(1)知AB=2AC,所以解得AC=1.
思维升华
(1)判断三角形形状的方法
①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
②化角:通过三角恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用A+B+C=π这个结论.
(2)求解几何计算问题要注意
①根据已知的边角画出图形并在图中标示;
②选择在某个三角形中运用正弦定理或余弦定理.
跟踪训练3 (1)在△ABC中,内角A,B,C所对的边长分别是a,b,c,若c-acos B=(2a-b)cos A,则△ABC的形状为
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
答案
解析
∵c-acos B=(2a-b)cos A,C=π-(A+B),
∴由正弦定理得sin C-sin Acos B=2sin Acos A-sin Bcos A,
∴sin Acos B+cos Asin B-sin Acos B=2sin Acos A-sin Bcos A,
∴cos A(sin B-sin A)=0,∴cos A=0或sin B=sin A,
∴A= 或B=A或B=π-A(舍去),
∴△ABC为等腰或直角三角形.
(2)(2015·课标全国Ⅰ)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
答案
解析
如图所示,延长BA与CD相交于点E,
过点C作CF∥AD交AB于点F,则BF
在等腰三角形ECB中,∠CEB=30°,∠ECB=75°,
二审结论会转换
审题路线图系列
(1)求cos A的值;
规范解答
审题路线图
返回
返回
课堂练习
A.135° B.105° C.45° D.75°
答案
解析
√
又由题知,BC
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
√
答案
解析
3.设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,且sin2B=sin2C,则△ABC的形状为
A.等腰三角形 B.锐角三角形
C.直角三角形 D.等腰直角三角形
√
答案
解析
由bcos C+ccos B=asin A,得sin Bcos C+sin Ccos B=sin2A,
∴sin(B+C)=sin2A,
即sin A=sin2A,在三角形中sin A≠0,∴sin A=1,∴A=90°,
由sin2B=sin2C,知b=c,
综上可知△ABC为等腰直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
√
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
由余弦定理,得BD2=CB2+CD2-2CD·CBcos ∠DCB=4,解得BD=2.
∴∠BDC=135°,∠ADC=45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
答案
解析
√
即a2+c2-b2=ac,
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
答案
解析
解得sin B=1,所以B=90°,
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
8.在△ABC中,角A,B,C的对边分别为a,b,c.若(a2+c2-b2)tan B=
ac,则角B的值为 .
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
答案
解析
8
又b-c=2,∴b2-2bc+c2=4,b2+c2=52,
∴a=8.
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
*10.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足asin B=
bcos A.若a=4,则△ABC周长的最大值为 .
答案
解析
12
由余弦定理得a2=16=b2+c2-2bccos A
则(b+c)2≤64,即b+c≤8(当且仅当b=c=4时等号成立),
∴△ABC周长=a+b+c=4+b+c≤12,即最大值为12.
1
2
3
4
5
6
7
8
9
10
11
12
13
11.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足
csin A=acos C.
(1)求角C的大小.
解答
由正弦定理,得sin Csin A=sin Acos C,
因为0
从而sin C=cos C,
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)求 sin A-cos(B+ )的最大值,并求取得最大值时角A,B的大小.
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
12.(2015·陕西)△ABC的内角A,B,C 所对的边分别为a,b,c.向量m=(a, )与n=(cos A,sin B)平行.
(1)求A;
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
解答
方法一 由余弦定理,得a2=b2+c2-2bccos A,
得7=4+c2-2c,即c2-2c-3=0,
因为c>0,所以c=3,
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)求角A和角B的大小;
解答
即sin B=1+cos C,则cos C<0,即C为钝角,
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)求△ABC的面积.
解答
由(1)知,a=b,
解得b=2,
