1.2 解三角形的应用举例距离问题 课件(74张PPT)
文档属性
| 名称 | 1.2 解三角形的应用举例距离问题 课件(74张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-13 07:48:27 | ||
图片预览









文档简介
(共74张PPT)
马新作室
点击
返回目录
1.2应用举例
第1课时解三角形的实际应用举例—距离问题
目
标能够运用正、余弦定理的知识和方法求解距离
问题
定
2.从实际问题中抽象出数学模型(即画出三角形)
位
1.本课的重点是能够运用正、余弦定理的知识和方
重法求解距离问题
点|2.本课的难点是从实际间题中抽象出数学模型(即
难点
画出三角形).
基础梳理
1.基线
在测量上,我们根据测量需要适当确定的线段叫做基线
2.选择基线的原则
在测量过程中,要根据实际需要选取合适的基线长度,使
测量具有较高的精确度.一般来说,基线越长,测量的精
确度越高
思考运用
1.如果知道一个三角形的三个角,是否可以解出这个三角形
提示:不可以.要解一个三角形,至少知道这个三角形的
一条边长
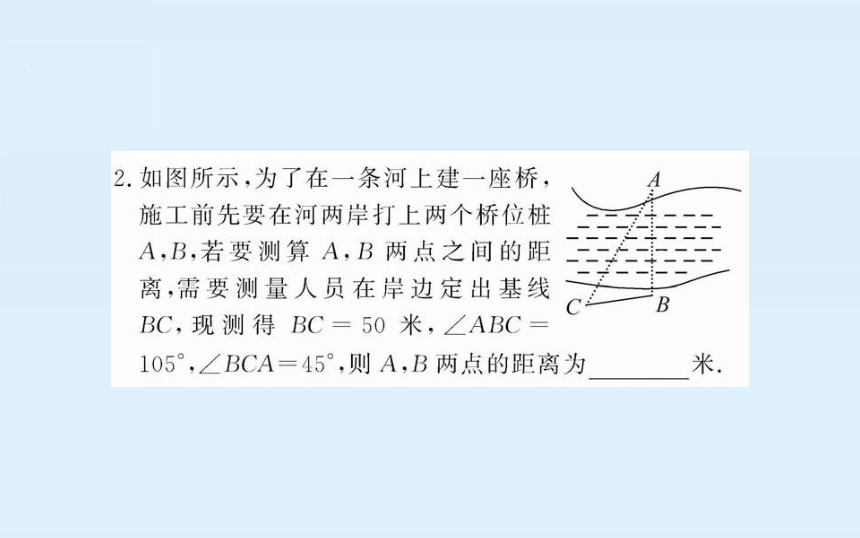
2.如图所示,为了在一条河上建一座桥,
施工前先要在河两岸打上两个桥位桩
二:二二
A,B,若要测算A,B两点之间的距
离,需要测量人员在岸边定出基线
BC,现测得BC=50米,∠ABC
105°,∠BCA=45°,则A,B两点的距离为
米
【解析】在△ABC中,BC=50米,∠ABC=105°,∠BCA
=45°,所以∠BAC=180—∠ABC-∠BCA=180
105°-45°=30°
由正弦定理得AB
BO
sin∠
BCA
Sin∠BAC
所以ABBC×sin∠BCA_50×sim45°
sin∠BAC
sin30°
50×y2
50√2(米)
2
答案:50√2
3.A,B两点间有一小山,先选定能直接到达点A,B的点
C,并测得AC=60m,BC=160m,∠ACB=60°,则A,B
两点间的距离为
解析】在△ABC中,由余弦定理得
AB=√602+1602-2×60×160c0s60°=140(m).
答案:140m
知识点拨
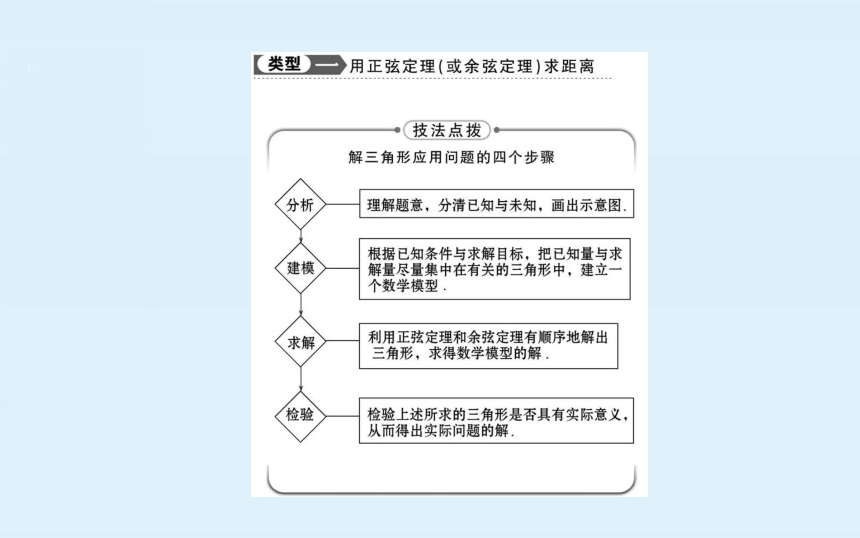
1.测量距离问题包括两种情况
(1)测量一个可到达的点到一个不可到达的点之间的
距离;
(2)测量两个不可到达点之间的距离
第一种情况实际上就是已知三角形两个角和一边的解三
角形问题,用正弦定理即可解决(如图1);对于第二种情
况,首先把求不可到达的两点A,B之间的距离转化为应
用正弦定理求三角形的边长问题,然后把BC,AC转化
为测量可到达的点与不可到达的点之间的距离问题(如
图2).
B
图1
C
图2
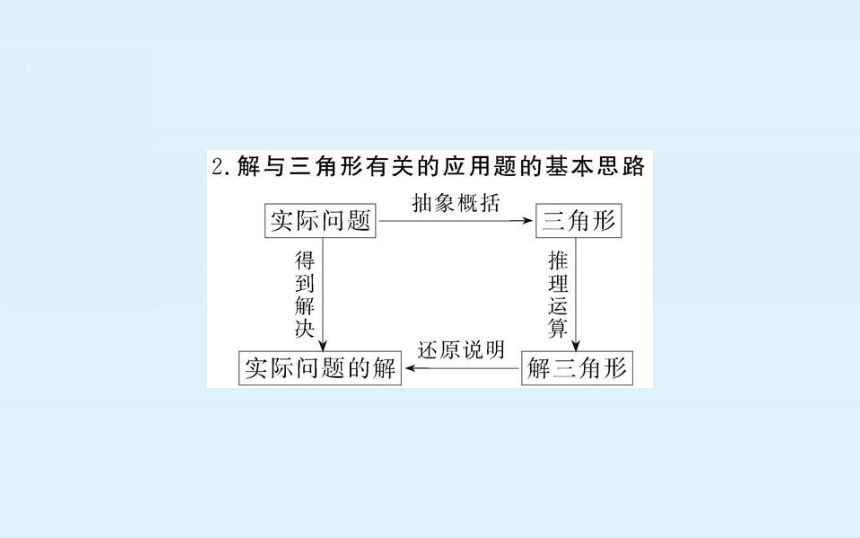
2.解与三角形有关的应用题的基本思路
实际问题抽象概括
角形
得到解决
推理运算
还原说明
实际问题的解
解三角形
马新作室
点击
返回目录
1.2应用举例
第1课时解三角形的实际应用举例—距离问题
目
标能够运用正、余弦定理的知识和方法求解距离
问题
定
2.从实际问题中抽象出数学模型(即画出三角形)
位
1.本课的重点是能够运用正、余弦定理的知识和方
重法求解距离问题
点|2.本课的难点是从实际间题中抽象出数学模型(即
难点
画出三角形).
基础梳理
1.基线
在测量上,我们根据测量需要适当确定的线段叫做基线
2.选择基线的原则
在测量过程中,要根据实际需要选取合适的基线长度,使
测量具有较高的精确度.一般来说,基线越长,测量的精
确度越高
思考运用
1.如果知道一个三角形的三个角,是否可以解出这个三角形
提示:不可以.要解一个三角形,至少知道这个三角形的
一条边长
2.如图所示,为了在一条河上建一座桥,
施工前先要在河两岸打上两个桥位桩
二:二二
A,B,若要测算A,B两点之间的距
离,需要测量人员在岸边定出基线
BC,现测得BC=50米,∠ABC
105°,∠BCA=45°,则A,B两点的距离为
米
【解析】在△ABC中,BC=50米,∠ABC=105°,∠BCA
=45°,所以∠BAC=180—∠ABC-∠BCA=180
105°-45°=30°
由正弦定理得AB
BO
sin∠
BCA
Sin∠BAC
所以ABBC×sin∠BCA_50×sim45°
sin∠BAC
sin30°
50×y2
50√2(米)
2
答案:50√2
3.A,B两点间有一小山,先选定能直接到达点A,B的点
C,并测得AC=60m,BC=160m,∠ACB=60°,则A,B
两点间的距离为
解析】在△ABC中,由余弦定理得
AB=√602+1602-2×60×160c0s60°=140(m).
答案:140m
知识点拨
1.测量距离问题包括两种情况
(1)测量一个可到达的点到一个不可到达的点之间的
距离;
(2)测量两个不可到达点之间的距离
第一种情况实际上就是已知三角形两个角和一边的解三
角形问题,用正弦定理即可解决(如图1);对于第二种情
况,首先把求不可到达的两点A,B之间的距离转化为应
用正弦定理求三角形的边长问题,然后把BC,AC转化
为测量可到达的点与不可到达的点之间的距离问题(如
图2).
B
图1
C
图2
2.解与三角形有关的应用题的基本思路
实际问题抽象概括
角形
得到解决
推理运算
还原说明
实际问题的解
解三角形
