1.2 解三角形的应用举例高度、角度问题 课件(61张PPT)
文档属性
| 名称 | 1.2 解三角形的应用举例高度、角度问题 课件(61张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-13 07:49:38 | ||
图片预览








文档简介
(共61张PPT)
马新作室
点击
返回目录
举例—高度、角度问题
目
标巩固掌握正、余弦定理
定厘用正、余弦定理等知识和方法求解高度和角度
问题
位
题
重1.本课的重点是应用正、余弦定理等知识和方法求
点解高度和角度问题
难2.本课的难点是从实际问题中抽象出数学模型
点
基础梳理
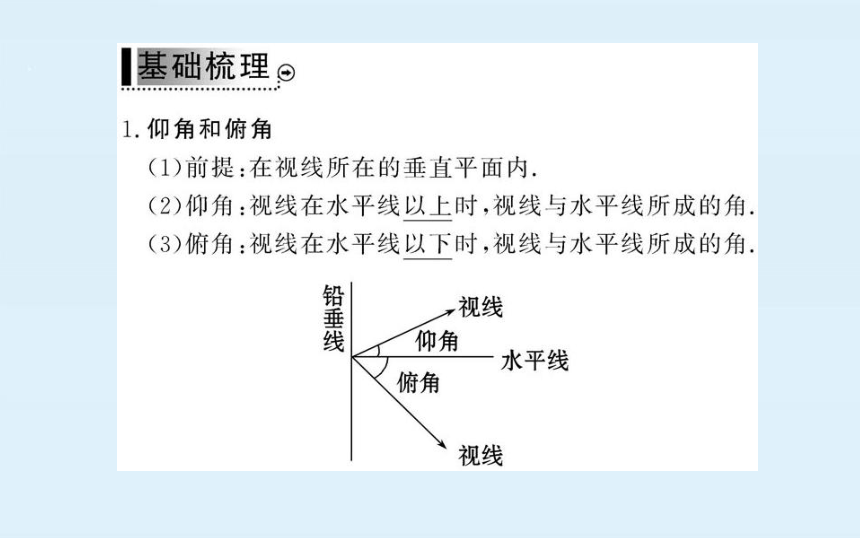
1角和俯角
(1)前提:在视线所在的垂直平面内.
(2)仰角:视线在水平线以上时,视线与水平线所成的角
(3)俯角:视线在水平线以下时,视线与水平线所成的角
铅垂线
→视线
仰角
水平线
俯角
视线
2.高度问题
测量顶部或底部不可到达的建筑物的高度问题,由于顶
部或底部不可到达,这类问题不能直接用解直角三角形
的方法解决,但可用正、余弦定理计算出建筑物顶部或底
部到一个可到达的点之间的距离,然后转化为解直角三
角形的问题
3.角度问题
测量角度就是在三角形内,利用正弦定理和余弦定理求
角的三角函数值,然后求角,再根据需要求所求的角
思考运用
为了测量某建筑物的高度所构造的三角形,其所在平面
与地面之间有什么关系
提示:为了测量某建筑物的高度所构造的三角形,其所在
平面与地面垂直
2.如图所示,甲,乙两楼相距20m,从
乙楼底望甲楼顶的仰角为60°,从甲
楼顶望乙楼顶的俯角为30°,则甲,
乙两楼的高分别是
A
30°
甲
乙
60°
B
解析】依题意有甲楼的高度
AB=20·tan60°=20√3(m)
又CM=DB=20m,∠CAM=60°,
所以AM=CM(m)
tango
故乙楼的高度CD=20√3
20340√3
答案:203m,403
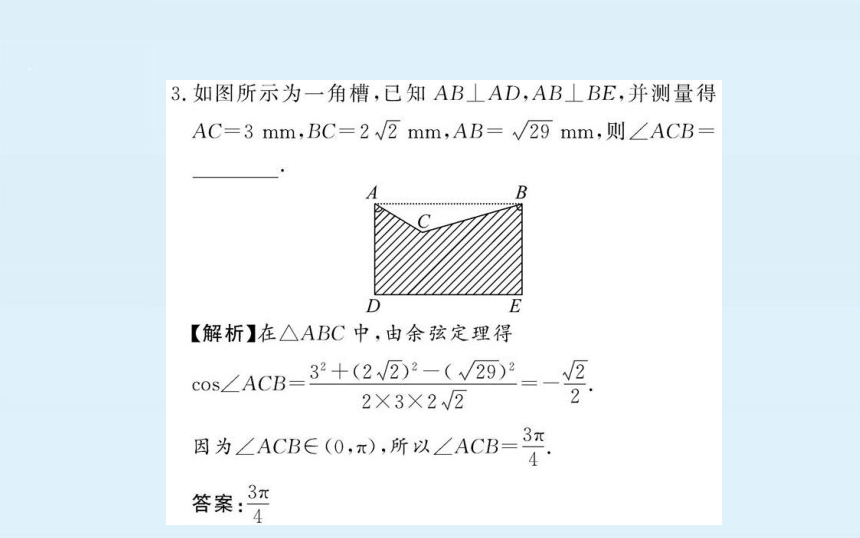
如图所示为一角槽,已知AB⊥AD,AB⊥BE,并测量得
AC=3mm,BC=2√2mm,AB=√29mm,则∠ACB
E
解析】在△ABC中,由余弦定理得
∠ACB
(2√2)
2×3×2√2
2
因为∠ACB∈(0,π),所以∠ACB
答案
知识点拨⊙
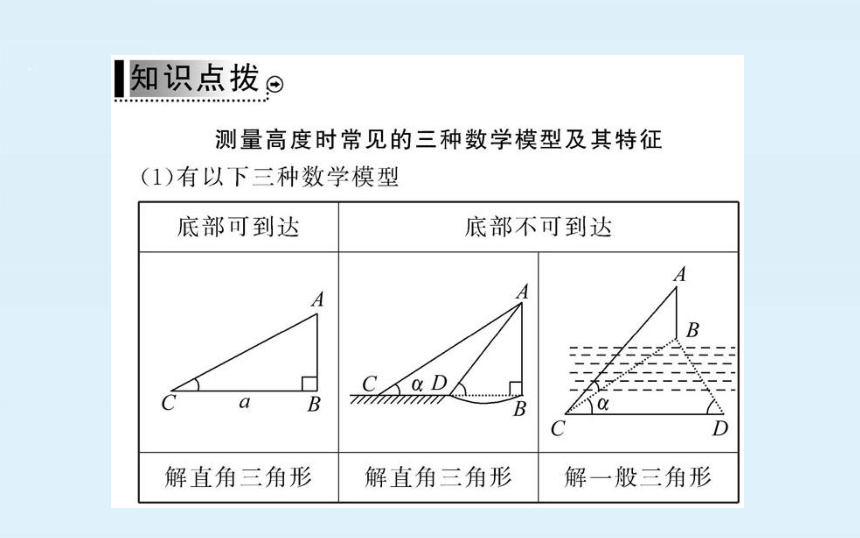
测量高度时常见的三种数学模型及其特征
(1)有以下三种数学模型
底部可到达
底部不可到达
A1B
△
解直角三角形解直角三角形解一般三角形
(2)特征
①底部可到达,此类问题可直接构造直角三角形
②底部不可到达,但仍在同一与地面垂直的平面内,此类
问题中两次观测点和所测垂线段的垂足在同一条直线
上,观测者一直向“目标物”前进
③底部不可到达,且不涉及与地面垂直的平面.此类问题
中观测者两次观测点所在直线不经过“目标物”
马新作室
点击
返回目录
举例—高度、角度问题
目
标巩固掌握正、余弦定理
定厘用正、余弦定理等知识和方法求解高度和角度
问题
位
题
重1.本课的重点是应用正、余弦定理等知识和方法求
点解高度和角度问题
难2.本课的难点是从实际问题中抽象出数学模型
点
基础梳理
1角和俯角
(1)前提:在视线所在的垂直平面内.
(2)仰角:视线在水平线以上时,视线与水平线所成的角
(3)俯角:视线在水平线以下时,视线与水平线所成的角
铅垂线
→视线
仰角
水平线
俯角
视线
2.高度问题
测量顶部或底部不可到达的建筑物的高度问题,由于顶
部或底部不可到达,这类问题不能直接用解直角三角形
的方法解决,但可用正、余弦定理计算出建筑物顶部或底
部到一个可到达的点之间的距离,然后转化为解直角三
角形的问题
3.角度问题
测量角度就是在三角形内,利用正弦定理和余弦定理求
角的三角函数值,然后求角,再根据需要求所求的角
思考运用
为了测量某建筑物的高度所构造的三角形,其所在平面
与地面之间有什么关系
提示:为了测量某建筑物的高度所构造的三角形,其所在
平面与地面垂直
2.如图所示,甲,乙两楼相距20m,从
乙楼底望甲楼顶的仰角为60°,从甲
楼顶望乙楼顶的俯角为30°,则甲,
乙两楼的高分别是
A
30°
甲
乙
60°
B
解析】依题意有甲楼的高度
AB=20·tan60°=20√3(m)
又CM=DB=20m,∠CAM=60°,
所以AM=CM(m)
tango
故乙楼的高度CD=20√3
20340√3
答案:203m,403
如图所示为一角槽,已知AB⊥AD,AB⊥BE,并测量得
AC=3mm,BC=2√2mm,AB=√29mm,则∠ACB
E
解析】在△ABC中,由余弦定理得
∠ACB
(2√2)
2×3×2√2
2
因为∠ACB∈(0,π),所以∠ACB
答案
知识点拨⊙
测量高度时常见的三种数学模型及其特征
(1)有以下三种数学模型
底部可到达
底部不可到达
A1B
△
解直角三角形解直角三角形解一般三角形
(2)特征
①底部可到达,此类问题可直接构造直角三角形
②底部不可到达,但仍在同一与地面垂直的平面内,此类
问题中两次观测点和所测垂线段的垂足在同一条直线
上,观测者一直向“目标物”前进
③底部不可到达,且不涉及与地面垂直的平面.此类问题
中观测者两次观测点所在直线不经过“目标物”
