北师大版数学四上交换律学习卡片学案(无答案)
文档属性
| 名称 | 北师大版数学四上交换律学习卡片学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-13 20:18:13 | ||
图片预览

文档简介
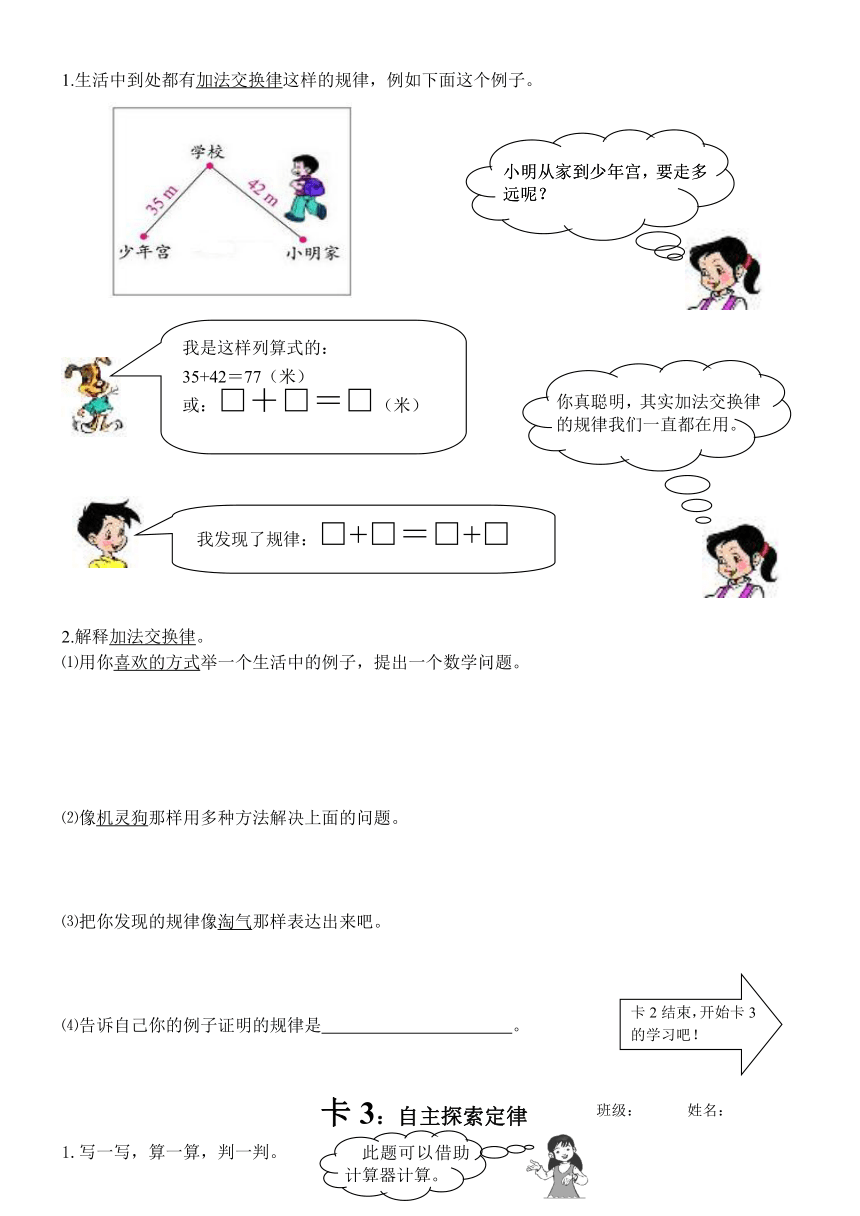
卡1:自主探索定律
1.快速计算下面各题。
20+80= 70+5=
7+12= 80+20=
60+15= 13+15=
56+21= 12+7=
25+3= 21+56=
2.仔细观察上面10个算式和结果,根据你的发现,将这些算式写成等式。
3.将这五组等式按照一定的标准分成两类,写在下面。
第一类: 第二类:
4.⑴请你按照淘气所写的样子再写出2组来,并仔细算一算和是不是一样。
□+□=□+□ □+□=□+□
⑵符合这种规律的算式能写完吗?请你尝试用图形、符号等表示出这些等式的规律。
5.上面这些等式反映出一个规律,你能用比较简练的语言把它概括出来吗?试着写一写!
6.
⑵这就是我们今天学习的加法交换律,请你再默读两遍!
卡2:举例说明规律
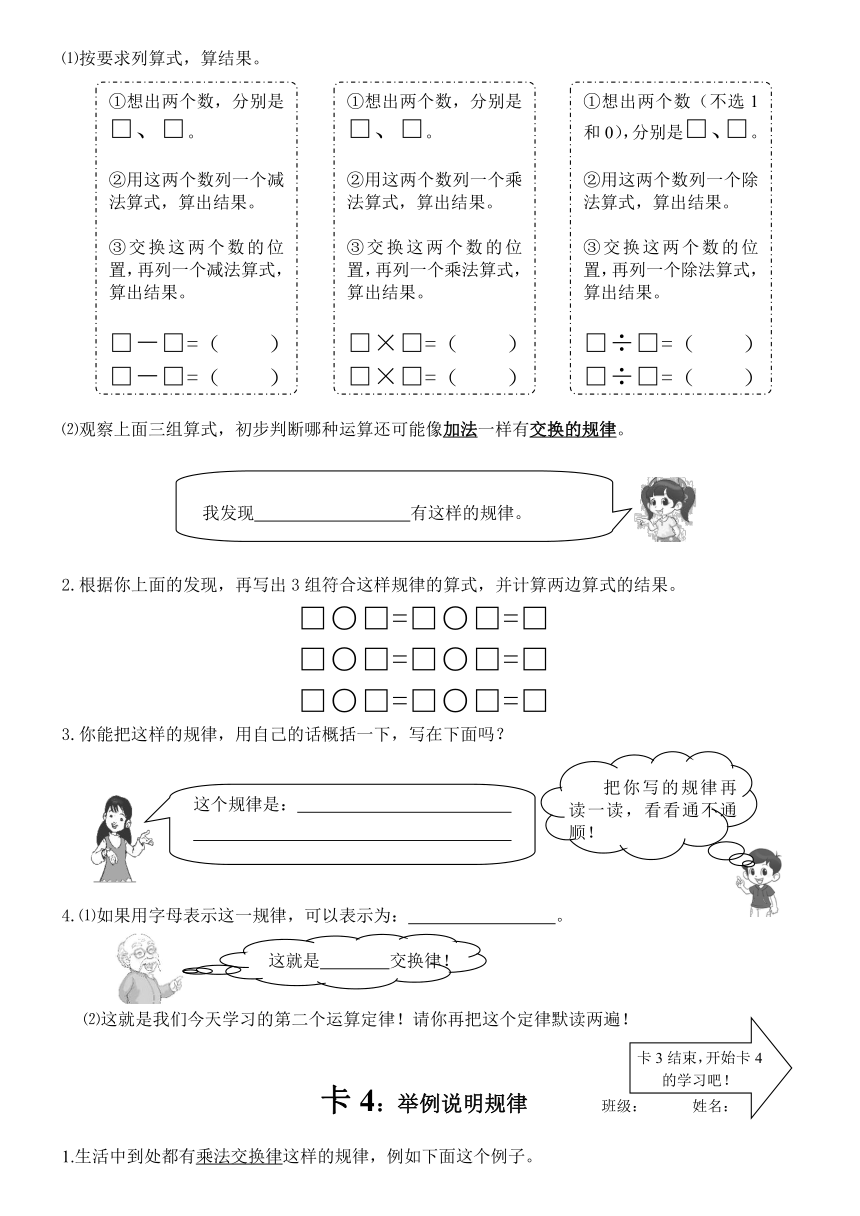
1.生活中到处都有加法交换律这样的规律,例如下面这个例子。
2.解释加法交换律。
⑴用你喜欢的方式举一个生活中的例子,提出一个数学问题。
⑵像机灵狗那样用多种方法解决上面的问题。
⑶把你发现的规律像淘气那样表达出来吧。
⑷告诉自己你的例子证明的规律是 。
卡3:自主探索定律
1.写一写,算一算,判一判。
⑴按要求列算式,算结果。
⑵观察上面三组算式,初步判断哪种运算还可能像加法一样有交换的规律。
2.根据你上面的发现,再写出3组符合这样规律的算式,并计算两边算式的结果。
□○□=□○□=□
□○□=□○□=□
□○□=□○□=□
3.你能把这样的规律,用自己的话概括一下,写在下面吗?
4.⑴如果用字母表示这一规律,可以表示为: 。
⑵这就是我们今天学习的第二个运算定律!请你再把这个定律默读两遍!
卡4:举例说明规律
1.生活中到处都有乘法交换律这样的规律,例如下面这个例子。
2.解释乘法交换律。
⑴用你喜欢的方式举一个生活中的例子,提出一个数学问题。
⑵像机灵狗那样用多种方法解决上面的问题。
⑶把你发现的规律像淘气那样表达出来吧。
⑷告诉自己你的例子证明的规律是 。
卡5:检测
1.运用加法交换律和乘法交换律填一填。
45+76 = □+ 45 45×102=102×□
28+13 = □+□ 296×200=□×□
□+□=□+□ □×□=□×□
6○42=42○6 23×( )=4×( )
2.下面的等式中哪些运用了交换律?请在后面的括号里画“√”。
35+25=25+35 ……………( )
240+120=430+110 ………( )
120×5=5×120 …………( )
6×4=3×8 ………………( )
卡6:应用运算定律
1.为了使计算更准确,我们有很多方法,现在你能说说这些方法的道理吗?
请你用竖式计算下列各题,并用运用加法交换律或乘法交换律进行验算。
918+395= 35×27=
2.⑴请你计算下面各题。
(3+7)× 23 23×(3+7)
⑵这两个算式可以写成等式吗?符合交换律的规律吗?
卡7:有趣的故事
加法交换律的故事——“朝三暮四”
乘法交换律的故事——“横七竖八”
卡8:提出你的问题
我发现 有这样的规律。
小明从家到少年宫,要走多远呢?
班级: 姓名:
淘气写的这个等式应该是哪一类呢?请你写在这类的下面。
我来写一个:12+9=9+12
这个规律是:
a +b=
这个规律是:
你真聪明,其实加法交换律的规律我们一直都在用。
结果一样的算式,中间可以用等号“=”连接起来,这样的式子叫作等式。
如:20+80=80+20
①想出两个数,分别是□、□。
②用这两个数列一个减法算式,算出结果。
③交换这两个数的位置,再列一个减法算式,算出结果。
□-□=( )
□-□=( )
①想出两个数,分别是□、□。
②用这两个数列一个乘法算式,算出结果。
③交换这两个数的位置,再列一个乘法算式,算出结果。
□×□=( )
□×□=( )
①想出两个数(不选1和0),分别是□、□。
②用这两个数列一个除法算式,算出结果。
③交换这两个数的位置,再列一个除法算式,算出结果。
□÷□=( )
□÷□=( )
这就是 交换律!
16×25=400
358+276=634
验
算:
验
算:
我不同意!
看到上面这两个故事,你是怎么想的?找个同学交流一下!你能不能再编几个符合加法交换律和乘法交换律的小故事?说给你的同学听一听!
我的问题是:
早上给你3个橡子,晚上再给你4个橡子。
其实都一样啊!横着看,每排有7人,有8排,这是8个7;竖着看,每列有8人,有7列,这是7个8.
7×8=8×7
哈哈,其实都一样啊!4+3=3+4
关于交换律的学习,你还有哪些问题?把它们记录下来,存到问题银行里吧!
那么,早上给你4个橡子,晚上再给你3个橡子!
横8竖7!
横7竖8!
参加体操表演的一共有多少人呢?
班级: 姓名:
□+□=□+□
□+□=□+□
□+□=□+□
□+□=□+□
□+□=□+□
这就是加法交换律。
把你写的规律再读一读,看看通不通顺!
班级: 姓名:
班级: 姓名:
把你写的规律再读一读,看看通不通顺!
班级: 姓名:
班级: 姓名:
验
算:
验
算:
班级: 姓名:
此题可以借助计算器计算。
我发现了规律:□×□=□×□
⑴用字母a,b表示两个数,刚才发现的规律就可以表示为:
我发现了规律:□+□=□+□
卡1结束,开始卡2的学习吧!
我是这样列算式的:
35+42=77(米)
或:□+□=□(米)
小明从家到少年宫,要走多远呢?
卡3结束,开始卡4的学习吧!
卡4结束了,开始完成检测卡吧!
我们一起学习了加法交换律和乘法交换律,你弄明白了吗?
再默默说一说什么是加法交换律,什么是乘法交换律!
检测合格后,进入到发展补充学习阶段吧!
恭喜你进入到发展阶段,这里有一些更难的问题,你敢接受挑战吗?
我同意!
卡2结束,开始卡3的学习吧!
班级: 姓名:
一共有多少块巧克力呢?
一排一排看是6个7,一列一列看是7个6,因此用乘法计算。
我是这样列算式的:
6×7=42(块)
或:□×□=□(块)
你真聪明,其实乘法交换律的规律我们一直都在用。
1.快速计算下面各题。
20+80= 70+5=
7+12= 80+20=
60+15= 13+15=
56+21= 12+7=
25+3= 21+56=
2.仔细观察上面10个算式和结果,根据你的发现,将这些算式写成等式。
3.将这五组等式按照一定的标准分成两类,写在下面。
第一类: 第二类:
4.⑴请你按照淘气所写的样子再写出2组来,并仔细算一算和是不是一样。
□+□=□+□ □+□=□+□
⑵符合这种规律的算式能写完吗?请你尝试用图形、符号等表示出这些等式的规律。
5.上面这些等式反映出一个规律,你能用比较简练的语言把它概括出来吗?试着写一写!
6.
⑵这就是我们今天学习的加法交换律,请你再默读两遍!
卡2:举例说明规律
1.生活中到处都有加法交换律这样的规律,例如下面这个例子。
2.解释加法交换律。
⑴用你喜欢的方式举一个生活中的例子,提出一个数学问题。
⑵像机灵狗那样用多种方法解决上面的问题。
⑶把你发现的规律像淘气那样表达出来吧。
⑷告诉自己你的例子证明的规律是 。
卡3:自主探索定律
1.写一写,算一算,判一判。
⑴按要求列算式,算结果。
⑵观察上面三组算式,初步判断哪种运算还可能像加法一样有交换的规律。
2.根据你上面的发现,再写出3组符合这样规律的算式,并计算两边算式的结果。
□○□=□○□=□
□○□=□○□=□
□○□=□○□=□
3.你能把这样的规律,用自己的话概括一下,写在下面吗?
4.⑴如果用字母表示这一规律,可以表示为: 。
⑵这就是我们今天学习的第二个运算定律!请你再把这个定律默读两遍!
卡4:举例说明规律
1.生活中到处都有乘法交换律这样的规律,例如下面这个例子。
2.解释乘法交换律。
⑴用你喜欢的方式举一个生活中的例子,提出一个数学问题。
⑵像机灵狗那样用多种方法解决上面的问题。
⑶把你发现的规律像淘气那样表达出来吧。
⑷告诉自己你的例子证明的规律是 。
卡5:检测
1.运用加法交换律和乘法交换律填一填。
45+76 = □+ 45 45×102=102×□
28+13 = □+□ 296×200=□×□
□+□=□+□ □×□=□×□
6○42=42○6 23×( )=4×( )
2.下面的等式中哪些运用了交换律?请在后面的括号里画“√”。
35+25=25+35 ……………( )
240+120=430+110 ………( )
120×5=5×120 …………( )
6×4=3×8 ………………( )
卡6:应用运算定律
1.为了使计算更准确,我们有很多方法,现在你能说说这些方法的道理吗?
请你用竖式计算下列各题,并用运用加法交换律或乘法交换律进行验算。
918+395= 35×27=
2.⑴请你计算下面各题。
(3+7)× 23 23×(3+7)
⑵这两个算式可以写成等式吗?符合交换律的规律吗?
卡7:有趣的故事
加法交换律的故事——“朝三暮四”
乘法交换律的故事——“横七竖八”
卡8:提出你的问题
我发现 有这样的规律。
小明从家到少年宫,要走多远呢?
班级: 姓名:
淘气写的这个等式应该是哪一类呢?请你写在这类的下面。
我来写一个:12+9=9+12
这个规律是:
a +b=
这个规律是:
你真聪明,其实加法交换律的规律我们一直都在用。
结果一样的算式,中间可以用等号“=”连接起来,这样的式子叫作等式。
如:20+80=80+20
①想出两个数,分别是□、□。
②用这两个数列一个减法算式,算出结果。
③交换这两个数的位置,再列一个减法算式,算出结果。
□-□=( )
□-□=( )
①想出两个数,分别是□、□。
②用这两个数列一个乘法算式,算出结果。
③交换这两个数的位置,再列一个乘法算式,算出结果。
□×□=( )
□×□=( )
①想出两个数(不选1和0),分别是□、□。
②用这两个数列一个除法算式,算出结果。
③交换这两个数的位置,再列一个除法算式,算出结果。
□÷□=( )
□÷□=( )
这就是 交换律!
16×25=400
358+276=634
验
算:
验
算:
我不同意!
看到上面这两个故事,你是怎么想的?找个同学交流一下!你能不能再编几个符合加法交换律和乘法交换律的小故事?说给你的同学听一听!
我的问题是:
早上给你3个橡子,晚上再给你4个橡子。
其实都一样啊!横着看,每排有7人,有8排,这是8个7;竖着看,每列有8人,有7列,这是7个8.
7×8=8×7
哈哈,其实都一样啊!4+3=3+4
关于交换律的学习,你还有哪些问题?把它们记录下来,存到问题银行里吧!
那么,早上给你4个橡子,晚上再给你3个橡子!
横8竖7!
横7竖8!
参加体操表演的一共有多少人呢?
班级: 姓名:
□+□=□+□
□+□=□+□
□+□=□+□
□+□=□+□
□+□=□+□
这就是加法交换律。
把你写的规律再读一读,看看通不通顺!
班级: 姓名:
班级: 姓名:
把你写的规律再读一读,看看通不通顺!
班级: 姓名:
班级: 姓名:
验
算:
验
算:
班级: 姓名:
此题可以借助计算器计算。
我发现了规律:□×□=□×□
⑴用字母a,b表示两个数,刚才发现的规律就可以表示为:
我发现了规律:□+□=□+□
卡1结束,开始卡2的学习吧!
我是这样列算式的:
35+42=77(米)
或:□+□=□(米)
小明从家到少年宫,要走多远呢?
卡3结束,开始卡4的学习吧!
卡4结束了,开始完成检测卡吧!
我们一起学习了加法交换律和乘法交换律,你弄明白了吗?
再默默说一说什么是加法交换律,什么是乘法交换律!
检测合格后,进入到发展补充学习阶段吧!
恭喜你进入到发展阶段,这里有一些更难的问题,你敢接受挑战吗?
我同意!
卡2结束,开始卡3的学习吧!
班级: 姓名:
一共有多少块巧克力呢?
一排一排看是6个7,一列一列看是7个6,因此用乘法计算。
我是这样列算式的:
6×7=42(块)
或:□×□=□(块)
你真聪明,其实乘法交换律的规律我们一直都在用。
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
