17.4 概率波与不确定关系 18张PPT
文档属性
| 名称 | 17.4 概率波与不确定关系 18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 895.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-13 14:55:41 | ||
图片预览






文档简介
17.4 概率波
17.5 不确定关系
第十七章 波粒二象性
光具有波动性,又有粒子性,即波粒二象性。
光在传播过程中表现出波动性,如干涉、衍射、偏振现象。
光在与物质发生作用时表现出粒子性,如光电效应,康普顿效应。
光子能量和动量为
二、经典的粒子和经典的波
1:经典的粒子的基本特征
⑴粒子有一定的空间大小、一定的质量和电荷量
⑵ 粒子的运动遵从牛顿第二定律
⑶粒子有确定的位置、速度以及时空中确定的轨道。
2:经典的波的基本特征
⑴在空间具有弥散性(可叠加分散)
⑵ 具有一定的频率、波长具有时空的周期性
光(波)具有粒子性
1.德布罗意假设
? 那么实物粒子也应具有波动性。
实物粒子具有波动性吗?
L.V. de Broglie (法,1892?1986)
从自然界的对称性出发,认为:
既然光(波)具有粒子性
1924.11.29德布洛意把题为“量子理论的研究”
的博士论文提交巴黎大学。
三、实物粒子的波动性
与粒子相联系的波称为物质波
或德布罗意波,
一个能量为E、动量为 p 的实物粒子同时
具有波动性,
他在论文中指出:
关系与光子一样:
它的波长?、频率? 和 E、p的
爱因斯坦 ─
德布罗意关系式
朗之万把德布洛意的文章寄给爱因斯坦,
爱因斯坦称赞说:
“揭开了自然界巨大帷幕的一角”
“瞧瞧吧,看来疯狂,可真是站得住脚呢”
论文获得了评委会的高度评价。
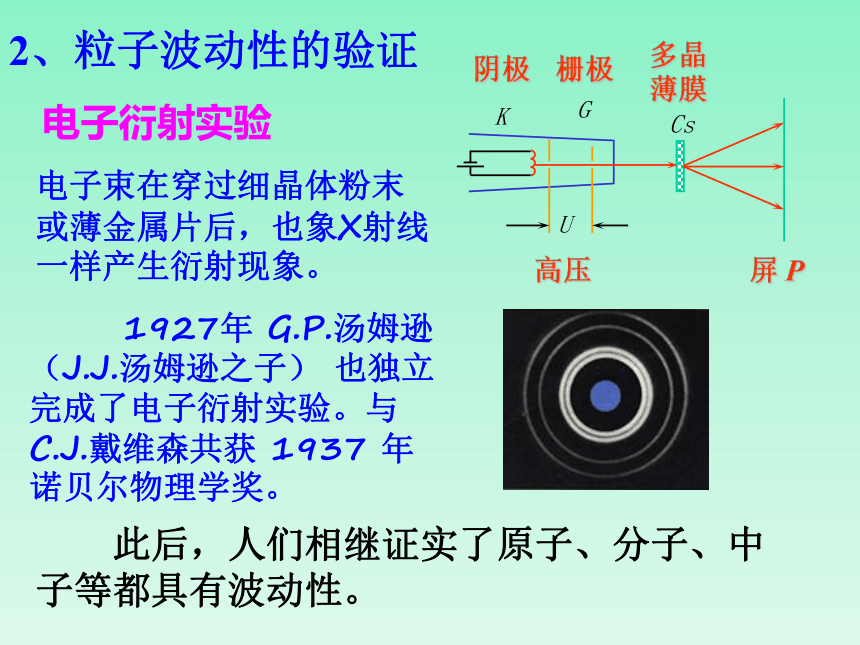
1927年 G.P.汤姆逊(J.J.汤姆逊之子) 也独立完成了电子衍射实验。与 C.J.戴维森共获 1937 年诺贝尔物理学奖。
电子衍射实验
电子束在穿过细晶体粉末或薄金属片后,也象X射线一样产生衍射现象。
此后,人们相继证实了原子、分子、中子等都具有波动性。
2、粒子波动性的验证
3、德布罗意波的统计解释
1926年德国物理学家波恩提出了概率波,认为个别微观粒子在何处出现有一定的偶然性,但大量粒子在空间何处出现的空间分布却服从一定的统计规律。
光的强弱对应于光子的数目,明纹处达到的光子数多,明纹表示光子达到的概率大。暗纹反之。
甲
丙
乙
一个一个电子依次入射双缝的衍射实验:
体现了粒子性
体现了波动性
通过上述实验可知:
虽然不能肯定某个光子落在哪一点,但在屏上各处明暗不同可以推知,光子落在各点的概率是不一样的,即光子落在明纹处的概率大,落在暗处的概率小。则光子在空间出现的概率可以通过衍射、干涉的明暗条纹这样的波动规律确定。
----------光是一种概率波。
物质波也具有波粒二象性,同样物质波也是概率波。
现象:1.单个粒子的位置是不确定的,但在某点附近出现的概率的大小可以由波动规律确定。
2.大量粒子,概率的分布导致确定的宏观结果。粒子数越多,规则的条纹越来越明显。
四、概率波
波动性是光子间相互作用的结果吗?
波动性不是光子间相互作用引起的,而是光子自身固有的性质
光是一种概率波
⑴不能确定某时刻某个光子落在哪个位置
⑵光子落在某一位置附近的概率可以确定,且光子在空间出现的概率可通过波动的规律确定。
光子在某位置出现的概率大,对大量光子来说达到该位置的光子数多,该位置出现明条纹。
反之出现暗条纹。
对实物粒子的波粒二象性的理解
1.与实物粒子相联系的物质波也是概率波,即单个粒子的位置是不确定的,但粒子在某点附近的概率的大小可以由波动的规律确定。
2.对大量粒子来说,概率大的位置达到的粒子数多,概率小的位置达到的粒子数少。
五、不确定性关系
经典力学:运动物体有完全确定的位置、动量、能量等。
微观粒子:位置、动量等具有不确定量(概率)。
电子衍射中的不确定性
一束电子以速度 v 沿 oy 轴射向狭缝。
电子在中央主极大区域出现的几率最大。
y
光强
△x表示粒子位置的不确定量,△p表示沿x轴的动量不确定量。
△x越小,明纹宽度越大,θ角越大,p的不确定量越大。衍射越明显。反之,p的不确定量越小。
不确定性关系
1.能否同时精确测出微粒的位置和动量?
微观粒子的位置和动量不能同时确定,若位置的不确定量减小了,动量的不确定量就会增大;若粒子有确定的动量,其位置就完全不确定。
2.不确定性关系
若用△x表示位置的不确定量,用△p表示粒子在x方向上的动量的不确定量,则:
不确定关系式表明:
1.微观粒子的坐标测得愈准确(? x?0) ,动量就愈不准确(?p ??) ;
微观粒子的动量测得愈准确(?p ?0) ,坐标就愈不准确(? x??) 。
但这里要注意,不确定关系
不是说微观粒子的坐标测不准;
也不是说微观粒子的动量测不准;
更不是说微观粒子的坐标和动量都测不准;
而是说微观粒子的坐标和动量不能同时测准。
这是因为微观粒子的坐标和动量本来就不同时具有确定量。
这本质上是微观粒子具有波粒二象性的必然反映。
由上讨论可知,不确定关系是自然界的一条客观规律,不是测量技术和主观能力的问题。
3.不确定关系提供了一个判据:
当不确定关系施加的限制可以忽略时,则可以用经典理论来研究粒子的运动。
当不确定关系施加的限制不可以忽略时,那只能用量子力学理论来处理问题。
2.为什么微观粒子的坐标和动量不能同时测准?
小结:
2.概率波
1.实物粒子的波动性
3.不确定性关系
17.5 不确定关系
第十七章 波粒二象性
光具有波动性,又有粒子性,即波粒二象性。
光在传播过程中表现出波动性,如干涉、衍射、偏振现象。
光在与物质发生作用时表现出粒子性,如光电效应,康普顿效应。
光子能量和动量为
二、经典的粒子和经典的波
1:经典的粒子的基本特征
⑴粒子有一定的空间大小、一定的质量和电荷量
⑵ 粒子的运动遵从牛顿第二定律
⑶粒子有确定的位置、速度以及时空中确定的轨道。
2:经典的波的基本特征
⑴在空间具有弥散性(可叠加分散)
⑵ 具有一定的频率、波长具有时空的周期性
光(波)具有粒子性
1.德布罗意假设
? 那么实物粒子也应具有波动性。
实物粒子具有波动性吗?
L.V. de Broglie (法,1892?1986)
从自然界的对称性出发,认为:
既然光(波)具有粒子性
1924.11.29德布洛意把题为“量子理论的研究”
的博士论文提交巴黎大学。
三、实物粒子的波动性
与粒子相联系的波称为物质波
或德布罗意波,
一个能量为E、动量为 p 的实物粒子同时
具有波动性,
他在论文中指出:
关系与光子一样:
它的波长?、频率? 和 E、p的
爱因斯坦 ─
德布罗意关系式
朗之万把德布洛意的文章寄给爱因斯坦,
爱因斯坦称赞说:
“揭开了自然界巨大帷幕的一角”
“瞧瞧吧,看来疯狂,可真是站得住脚呢”
论文获得了评委会的高度评价。
1927年 G.P.汤姆逊(J.J.汤姆逊之子) 也独立完成了电子衍射实验。与 C.J.戴维森共获 1937 年诺贝尔物理学奖。
电子衍射实验
电子束在穿过细晶体粉末或薄金属片后,也象X射线一样产生衍射现象。
此后,人们相继证实了原子、分子、中子等都具有波动性。
2、粒子波动性的验证
3、德布罗意波的统计解释
1926年德国物理学家波恩提出了概率波,认为个别微观粒子在何处出现有一定的偶然性,但大量粒子在空间何处出现的空间分布却服从一定的统计规律。
光的强弱对应于光子的数目,明纹处达到的光子数多,明纹表示光子达到的概率大。暗纹反之。
甲
丙
乙
一个一个电子依次入射双缝的衍射实验:
体现了粒子性
体现了波动性
通过上述实验可知:
虽然不能肯定某个光子落在哪一点,但在屏上各处明暗不同可以推知,光子落在各点的概率是不一样的,即光子落在明纹处的概率大,落在暗处的概率小。则光子在空间出现的概率可以通过衍射、干涉的明暗条纹这样的波动规律确定。
----------光是一种概率波。
物质波也具有波粒二象性,同样物质波也是概率波。
现象:1.单个粒子的位置是不确定的,但在某点附近出现的概率的大小可以由波动规律确定。
2.大量粒子,概率的分布导致确定的宏观结果。粒子数越多,规则的条纹越来越明显。
四、概率波
波动性是光子间相互作用的结果吗?
波动性不是光子间相互作用引起的,而是光子自身固有的性质
光是一种概率波
⑴不能确定某时刻某个光子落在哪个位置
⑵光子落在某一位置附近的概率可以确定,且光子在空间出现的概率可通过波动的规律确定。
光子在某位置出现的概率大,对大量光子来说达到该位置的光子数多,该位置出现明条纹。
反之出现暗条纹。
对实物粒子的波粒二象性的理解
1.与实物粒子相联系的物质波也是概率波,即单个粒子的位置是不确定的,但粒子在某点附近的概率的大小可以由波动的规律确定。
2.对大量粒子来说,概率大的位置达到的粒子数多,概率小的位置达到的粒子数少。
五、不确定性关系
经典力学:运动物体有完全确定的位置、动量、能量等。
微观粒子:位置、动量等具有不确定量(概率)。
电子衍射中的不确定性
一束电子以速度 v 沿 oy 轴射向狭缝。
电子在中央主极大区域出现的几率最大。
y
光强
△x表示粒子位置的不确定量,△p表示沿x轴的动量不确定量。
△x越小,明纹宽度越大,θ角越大,p的不确定量越大。衍射越明显。反之,p的不确定量越小。
不确定性关系
1.能否同时精确测出微粒的位置和动量?
微观粒子的位置和动量不能同时确定,若位置的不确定量减小了,动量的不确定量就会增大;若粒子有确定的动量,其位置就完全不确定。
2.不确定性关系
若用△x表示位置的不确定量,用△p表示粒子在x方向上的动量的不确定量,则:
不确定关系式表明:
1.微观粒子的坐标测得愈准确(? x?0) ,动量就愈不准确(?p ??) ;
微观粒子的动量测得愈准确(?p ?0) ,坐标就愈不准确(? x??) 。
但这里要注意,不确定关系
不是说微观粒子的坐标测不准;
也不是说微观粒子的动量测不准;
更不是说微观粒子的坐标和动量都测不准;
而是说微观粒子的坐标和动量不能同时测准。
这是因为微观粒子的坐标和动量本来就不同时具有确定量。
这本质上是微观粒子具有波粒二象性的必然反映。
由上讨论可知,不确定关系是自然界的一条客观规律,不是测量技术和主观能力的问题。
3.不确定关系提供了一个判据:
当不确定关系施加的限制可以忽略时,则可以用经典理论来研究粒子的运动。
当不确定关系施加的限制不可以忽略时,那只能用量子力学理论来处理问题。
2.为什么微观粒子的坐标和动量不能同时测准?
小结:
2.概率波
1.实物粒子的波动性
3.不确定性关系
