7.8 机械能守恒定律 21张PPT
文档属性
| 名称 | 7.8 机械能守恒定律 21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 635.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-13 00:00:00 | ||
图片预览





文档简介
7-8 机械能守恒定律
动能
重力势能
Ep=mgh
弹性势能
物体由于被举高度而具有的能量:
物体由于运动而具有的能量:
发生弹性形变的各物体各部之间由于有弹
力的相互作用而具有的能量。
知识回顾
动能定理
合力所做的总功等于物体动能的变化:
重力做的功等于物体重力势能的减少量:
弹力做的功等于弹性势能的减少量:
WG = EP1 - EP2
WF弹 = EP1 - EP2
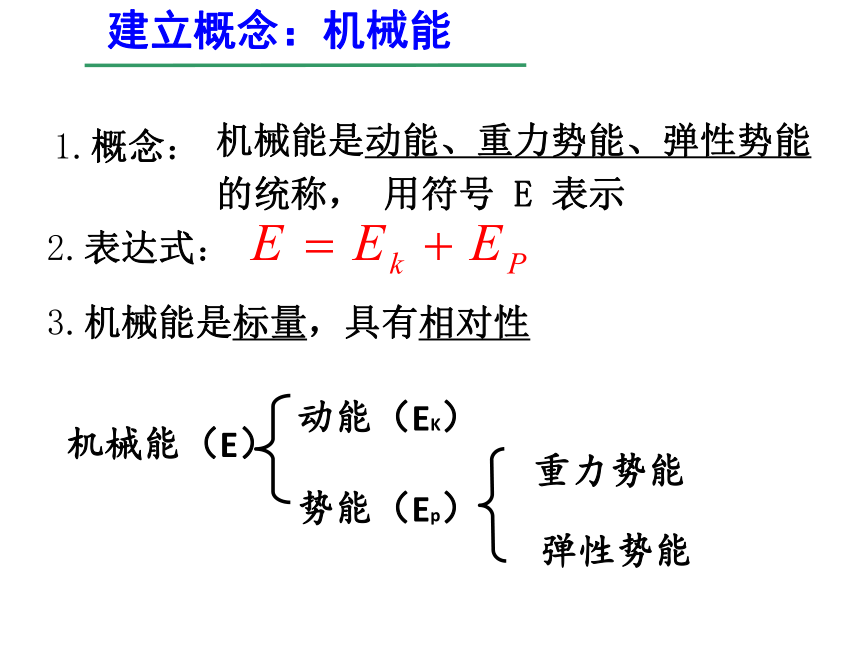
机械能是动能、重力势能、弹性势能的统称, 用符号 E 表示
3.机械能是标量,具有相对性
1.概念:
2.表达式:
建立概念:机械能
情景1:质量为m的物体自由下落时,经过高度h1处速度为v1,下落至高度为h2处速度为v2,不计空气阻力,分析此过程中机械能的变化.
问题情景与探究
A点
B点
由以上两式得
移项得
结论
地面为参考面
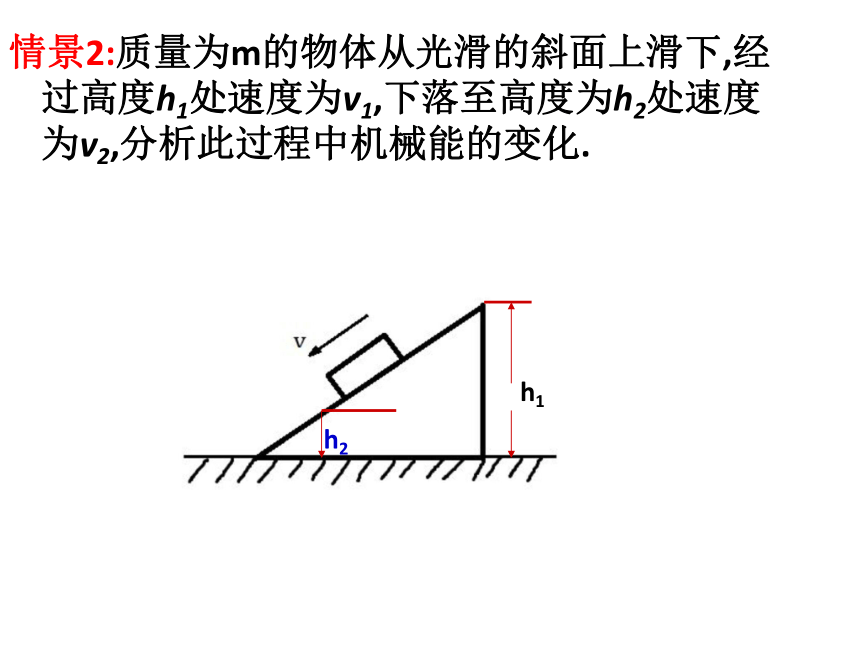
情景2:质量为m的物体从光滑的斜面上滑下,经过高度h1处速度为v1,下落至高度为h2处速度为v2,分析此过程中机械能的变化.
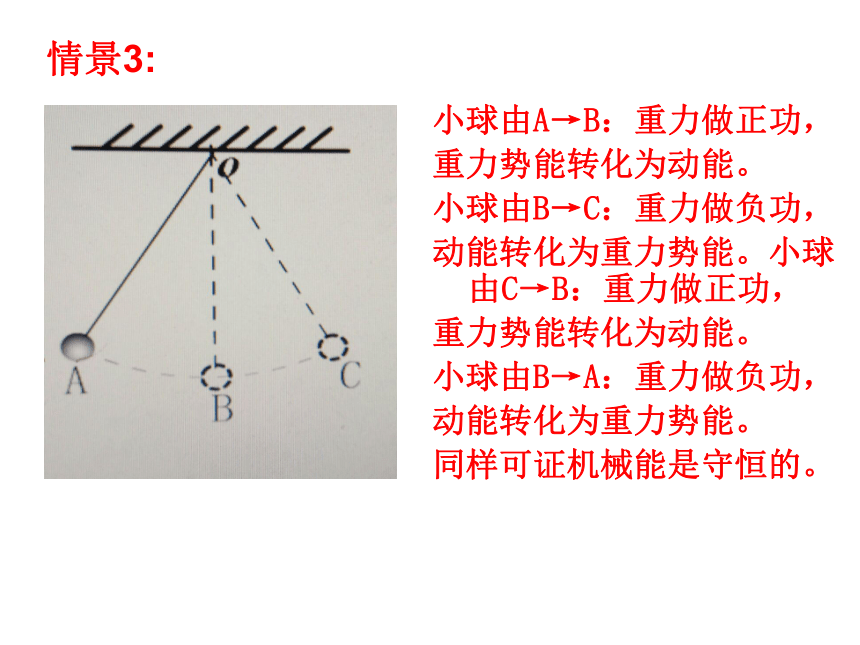
小球由A→B:重力做正功,
重力势能转化为动能。
小球由B→C:重力做负功,
动能转化为重力势能。小球由C→B:重力做正功,
重力势能转化为动能。
小球由B→A:重力做负功,
动能转化为重力势能。
同样可证机械能是守恒的。
情景3:
在只有重力做功的系统内,物体的动能和重力势能发生相互转化,机械能的总量保持不变。
即认为机械能守恒。
归纳情景1、2和3得出结论:
规律的发现
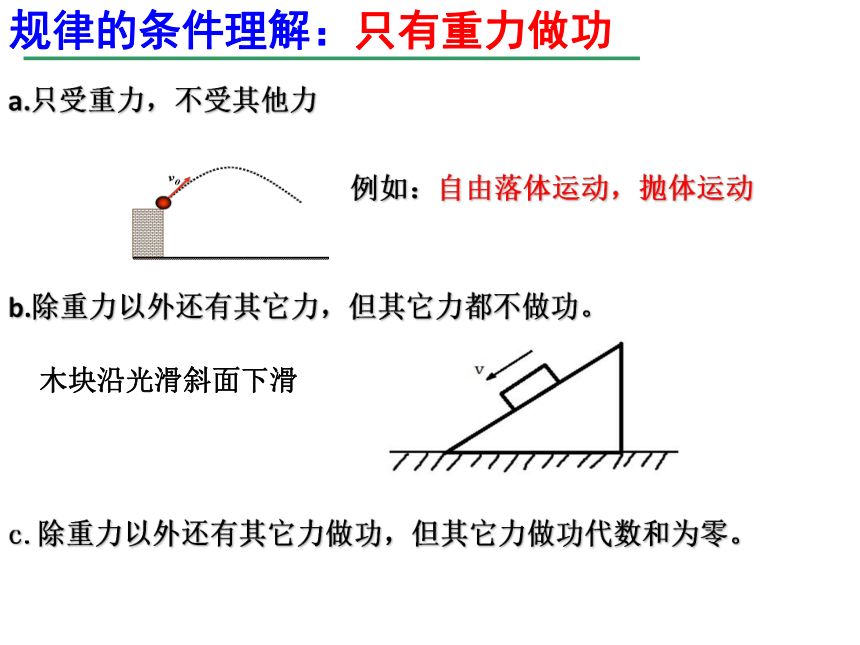
a.只受重力,不受其他力
b.除重力以外还有其它力,但其它力都不做功。
木块沿光滑斜面下滑
c.除重力以外还有其它力做功,但其它力做功代数和为零。
例如:自由落体运动,抛体运动
规律的条件理解:只有重力做功
A. 甲图中,物体A将弹簧压缩的过程中,A的机械能不守恒
B. 乙图中,物体B沿固定光滑的斜面上下滑时,物体B的机械能守恒
C.丙图中,小球沿水平面做匀速圆锥摆动时,小球的机械能守恒。
甲 乙 丙
(若斜面不固定呢?)
(2)对某一系统,只有重力和弹力做功,其它力不做功或做功的和为0
甲图中,物体A将弹簧压缩的过程中,A的机械能不守恒,但A和弹簧组成的系统机械能守恒。
乙图中,地面光滑,物体沿不固定光滑斜面下滑时,物体B的机械能不守恒,但B与斜面组成的系统机械能守恒。
1.A的机械能守恒吗?B的机械能守恒吗?
如果不守恒,是增加还是减少?
2.A、B组成的系统机械能守不守恒?
A物体机械能的增加量等于B物体机械能的减少量:△EA= -△EB
应用练习
A和地球为系统: T1是系统的外力,对系统做正功,系统机械能增加。
A、B系统的机械能守恒: T1和T2做功的代数和为零。
B和地球为系统: T2是系统的外力,对系统做负功,系统机械能增加。
练习:除1外都不计空气阻力,哪些情况机械能是守恒的?
巩固练习
5.抛出的铅球在空中运动
不守恒
守恒
不守恒
守恒
守恒
F1
弹簧振子实验
实验分析
小球由A→O:弹力做正功,
弹性势能转化为动能。
小球由O→B:弹力做负功,
动能转化为弹性势能。
实验结论:只有弹力做功的情况下,动能与弹性势能可以发生相互转化,动能和弹性势能的总和不变。
问题情景与继续探究
在只有重力或弹力做功的系统内,物体的动能和势能发生相互转化,机械能的总量保持不变。
:机械能守恒定律
注意:机械能守恒是指在一个过程中的每一个时刻机械能都相等,仅根据两个位置的机械能相等并不能直接得到这个过程的机械能守恒.
规律的发现
只有重力或系统内弹簧弹力做功,其它力不做功。其它力做功改变系统机械能!
A.从做功角度分析
B.从能量转化角度分析
只有系统内动能和势能相互转化,无其它形式能量之间(如内能)转化
机能守恒条件的归纳
①明确研究对象(物体或者系统)
②明确研究对象的运动过程,分析研究对象的受力情况以及各力做功的情况,判断机械能是否守恒
③选取参考平面(零势能面),并确定研究对象在过程中的始末机械能
④根据机械能守恒定律列出方程进行求解,有时不够时再辅之以其它方程
用机械能守恒定律解题步骤
2.一个轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面肯弹簧保持原长的A点无初速度释放,让它自由下摆,不计空气阻力,在重物由A摆到最低点的过程中,
A、重物的重力势能减少。
B、重物的重力势能增加。
C、重物的机械能不变。
D、重物的机械能减少。
AD
球和弹簧组成的系统机械能守恒
1.下列关于机械能是否守恒的叙述正确的是
A、做匀速直线运动的物体机械能一定守恒。
B、做匀变速直线运动的物体的机械能可能守恒。
C、合外力对物体做功为零时机机械能守恒。
D、只有重力对物体做功,物体的机械能一定守恒。
BD
物体的机械能是否守恒与物体的运动无关
应用练习
3.如图所示,桌面高为h,质量为m的
小球从离桌面高H处自由落下,不计空
气阻力,假设地面处的重力势能为零,
则小球落到地面前瞬间的机械能为
A.mgh B.mgH
C.mg(H+h) D.mg(H-h)
C
机械能(E=EK+EP)守恒定律:
(1)内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
(3)条件:只有重力、弹力做功
(2)表达式:EK2+EP2=EK1+EP1
mgh2+mv22/2=mgh1+mv12/2
本节总结
机械能守恒的三种表达式
2、系统改变的总势能等于系统改变的总动能,
即 -ΔEP=ΔEK
3、若系统只有A、B两物体,则A改变的机械能等于B改变的机械能,即 - ΔEA= ΔEB
动能
重力势能
Ep=mgh
弹性势能
物体由于被举高度而具有的能量:
物体由于运动而具有的能量:
发生弹性形变的各物体各部之间由于有弹
力的相互作用而具有的能量。
知识回顾
动能定理
合力所做的总功等于物体动能的变化:
重力做的功等于物体重力势能的减少量:
弹力做的功等于弹性势能的减少量:
WG = EP1 - EP2
WF弹 = EP1 - EP2
机械能是动能、重力势能、弹性势能的统称, 用符号 E 表示
3.机械能是标量,具有相对性
1.概念:
2.表达式:
建立概念:机械能
情景1:质量为m的物体自由下落时,经过高度h1处速度为v1,下落至高度为h2处速度为v2,不计空气阻力,分析此过程中机械能的变化.
问题情景与探究
A点
B点
由以上两式得
移项得
结论
地面为参考面
情景2:质量为m的物体从光滑的斜面上滑下,经过高度h1处速度为v1,下落至高度为h2处速度为v2,分析此过程中机械能的变化.
小球由A→B:重力做正功,
重力势能转化为动能。
小球由B→C:重力做负功,
动能转化为重力势能。小球由C→B:重力做正功,
重力势能转化为动能。
小球由B→A:重力做负功,
动能转化为重力势能。
同样可证机械能是守恒的。
情景3:
在只有重力做功的系统内,物体的动能和重力势能发生相互转化,机械能的总量保持不变。
即认为机械能守恒。
归纳情景1、2和3得出结论:
规律的发现
a.只受重力,不受其他力
b.除重力以外还有其它力,但其它力都不做功。
木块沿光滑斜面下滑
c.除重力以外还有其它力做功,但其它力做功代数和为零。
例如:自由落体运动,抛体运动
规律的条件理解:只有重力做功
A. 甲图中,物体A将弹簧压缩的过程中,A的机械能不守恒
B. 乙图中,物体B沿固定光滑的斜面上下滑时,物体B的机械能守恒
C.丙图中,小球沿水平面做匀速圆锥摆动时,小球的机械能守恒。
甲 乙 丙
(若斜面不固定呢?)
(2)对某一系统,只有重力和弹力做功,其它力不做功或做功的和为0
甲图中,物体A将弹簧压缩的过程中,A的机械能不守恒,但A和弹簧组成的系统机械能守恒。
乙图中,地面光滑,物体沿不固定光滑斜面下滑时,物体B的机械能不守恒,但B与斜面组成的系统机械能守恒。
1.A的机械能守恒吗?B的机械能守恒吗?
如果不守恒,是增加还是减少?
2.A、B组成的系统机械能守不守恒?
A物体机械能的增加量等于B物体机械能的减少量:△EA= -△EB
应用练习
A和地球为系统: T1是系统的外力,对系统做正功,系统机械能增加。
A、B系统的机械能守恒: T1和T2做功的代数和为零。
B和地球为系统: T2是系统的外力,对系统做负功,系统机械能增加。
练习:除1外都不计空气阻力,哪些情况机械能是守恒的?
巩固练习
5.抛出的铅球在空中运动
不守恒
守恒
不守恒
守恒
守恒
F1
弹簧振子实验
实验分析
小球由A→O:弹力做正功,
弹性势能转化为动能。
小球由O→B:弹力做负功,
动能转化为弹性势能。
实验结论:只有弹力做功的情况下,动能与弹性势能可以发生相互转化,动能和弹性势能的总和不变。
问题情景与继续探究
在只有重力或弹力做功的系统内,物体的动能和势能发生相互转化,机械能的总量保持不变。
:机械能守恒定律
注意:机械能守恒是指在一个过程中的每一个时刻机械能都相等,仅根据两个位置的机械能相等并不能直接得到这个过程的机械能守恒.
规律的发现
只有重力或系统内弹簧弹力做功,其它力不做功。其它力做功改变系统机械能!
A.从做功角度分析
B.从能量转化角度分析
只有系统内动能和势能相互转化,无其它形式能量之间(如内能)转化
机能守恒条件的归纳
①明确研究对象(物体或者系统)
②明确研究对象的运动过程,分析研究对象的受力情况以及各力做功的情况,判断机械能是否守恒
③选取参考平面(零势能面),并确定研究对象在过程中的始末机械能
④根据机械能守恒定律列出方程进行求解,有时不够时再辅之以其它方程
用机械能守恒定律解题步骤
2.一个轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面肯弹簧保持原长的A点无初速度释放,让它自由下摆,不计空气阻力,在重物由A摆到最低点的过程中,
A、重物的重力势能减少。
B、重物的重力势能增加。
C、重物的机械能不变。
D、重物的机械能减少。
AD
球和弹簧组成的系统机械能守恒
1.下列关于机械能是否守恒的叙述正确的是
A、做匀速直线运动的物体机械能一定守恒。
B、做匀变速直线运动的物体的机械能可能守恒。
C、合外力对物体做功为零时机机械能守恒。
D、只有重力对物体做功,物体的机械能一定守恒。
BD
物体的机械能是否守恒与物体的运动无关
应用练习
3.如图所示,桌面高为h,质量为m的
小球从离桌面高H处自由落下,不计空
气阻力,假设地面处的重力势能为零,
则小球落到地面前瞬间的机械能为
A.mgh B.mgH
C.mg(H+h) D.mg(H-h)
C
机械能(E=EK+EP)守恒定律:
(1)内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
(3)条件:只有重力、弹力做功
(2)表达式:EK2+EP2=EK1+EP1
mgh2+mv22/2=mgh1+mv12/2
本节总结
机械能守恒的三种表达式
2、系统改变的总势能等于系统改变的总动能,
即 -ΔEP=ΔEK
3、若系统只有A、B两物体,则A改变的机械能等于B改变的机械能,即 - ΔEA= ΔEB
