江苏省高邮市阳光双语初中2019年八年级数学第9章《中心对称图形-平行四边形》单元测试(含答案)
文档属性
| 名称 | 江苏省高邮市阳光双语初中2019年八年级数学第9章《中心对称图形-平行四边形》单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 144.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-12 21:37:23 | ||
图片预览

文档简介
八年级数学第9章《中心对称图形-平行四边形》同步测试
选择题:
1、下列说法中,正确个数有( )
①对顶角相等;
②两直线平行,同旁内角相等;
③对角线互相垂直的四边形为菱形;
④对角线互相垂直平分且相等的四边形为正方形.
A.1个 B.2个 C.3个 D.4个
2、已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
3、在平行四边形ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
4、如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A.50° B.40° C.30° D.20°
5、如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDF
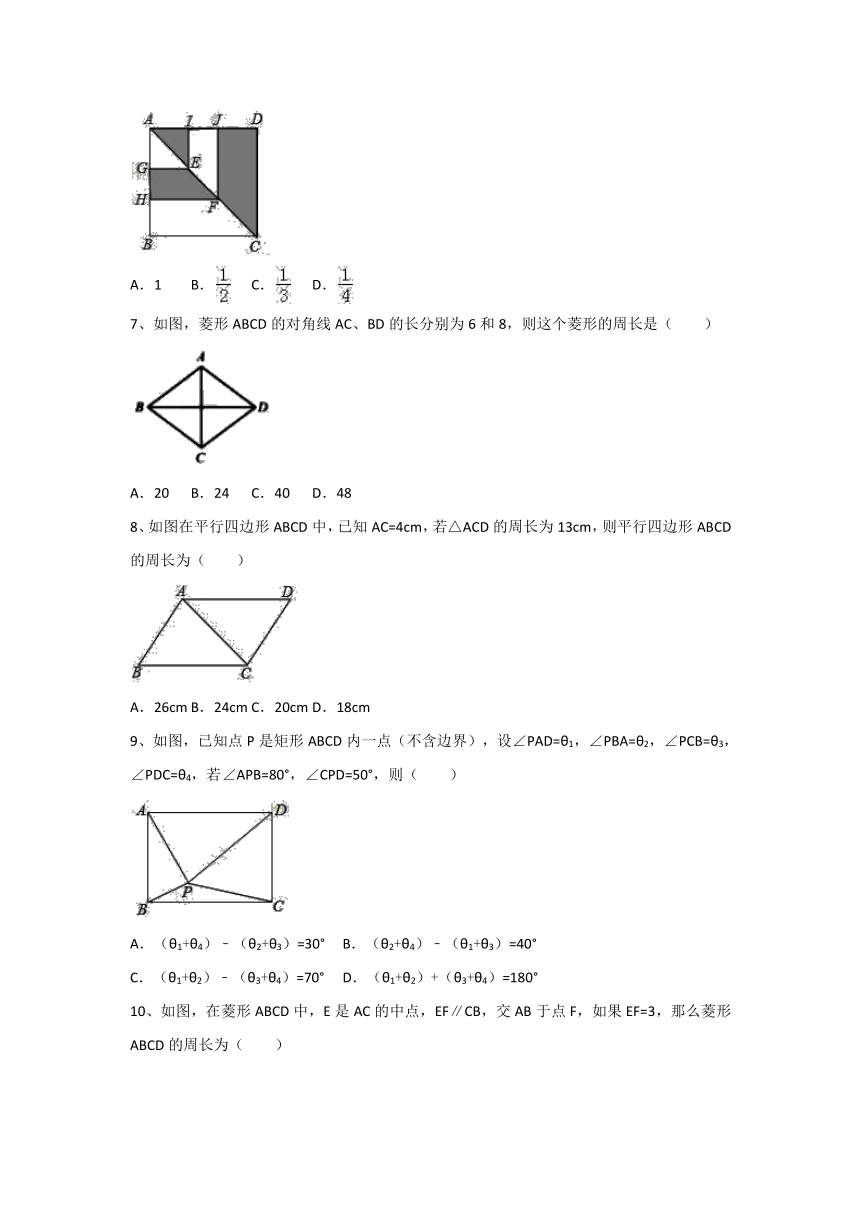
6、如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
A.1 B. C. D.
7、如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
8、如图在平行四边形ABCD中,已知AC=4cm,若△ACD的周长为13cm,则平行四边形ABCD的周长为( )
A.26cm B.24cm C.20cm D.18cm
9、如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=θ1,∠PBA=θ2,∠PCB=θ3,∠PDC=θ4,若∠APB=80°,∠CPD=50°,则( )
A.(θ1+θ4)﹣(θ2+θ3)=30° B.(θ2+θ4)﹣(θ1+θ3)=40°
C.(θ1+θ2)﹣(θ3+θ4)=70° D.(θ1+θ2)+(θ3+θ4)=180°
10、如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A.24 B.18 C.12 D.9
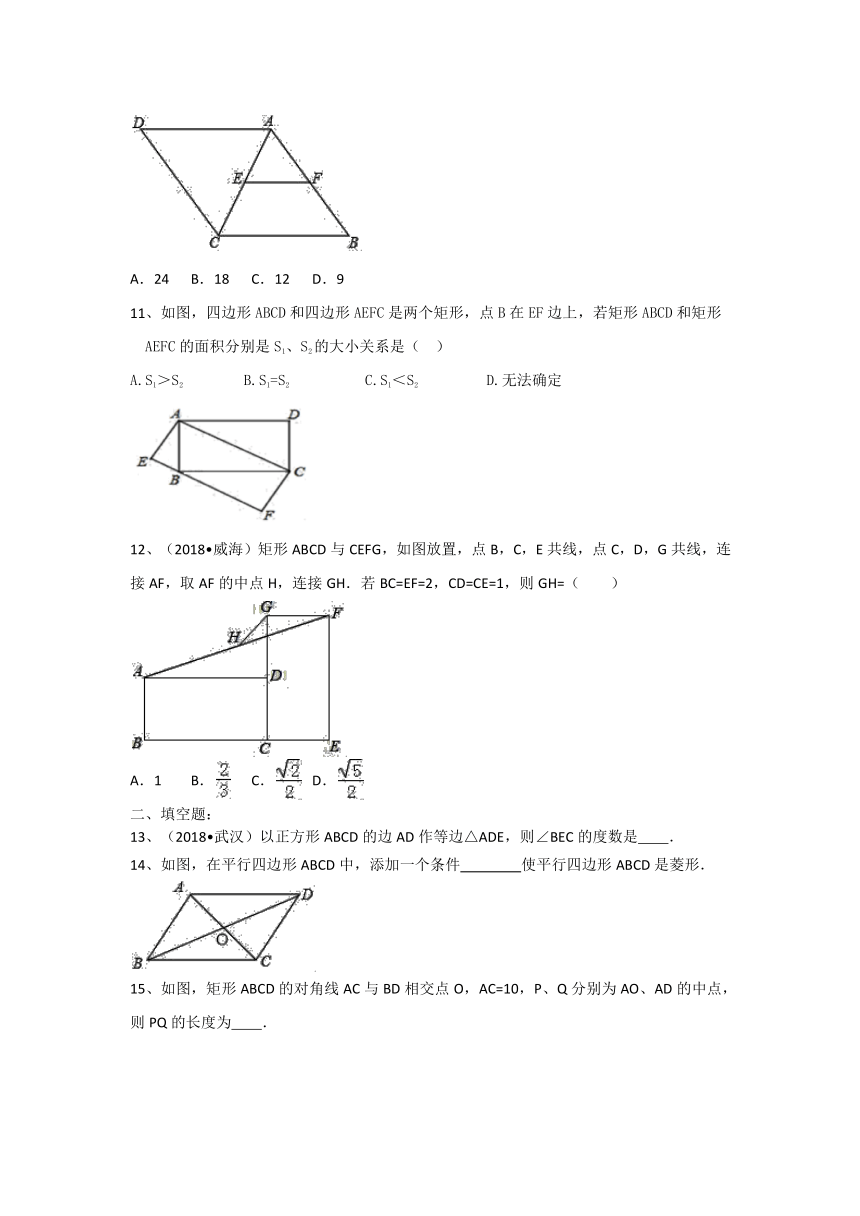
11、如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
12、(2018?威海)矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1 B. C. D.
二、填空题:
13、(2018?武汉)以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .
14、如图,在平行四边形ABCD中,添加一个条件 使平行四边形ABCD是菱形.
15、如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的长度为 .
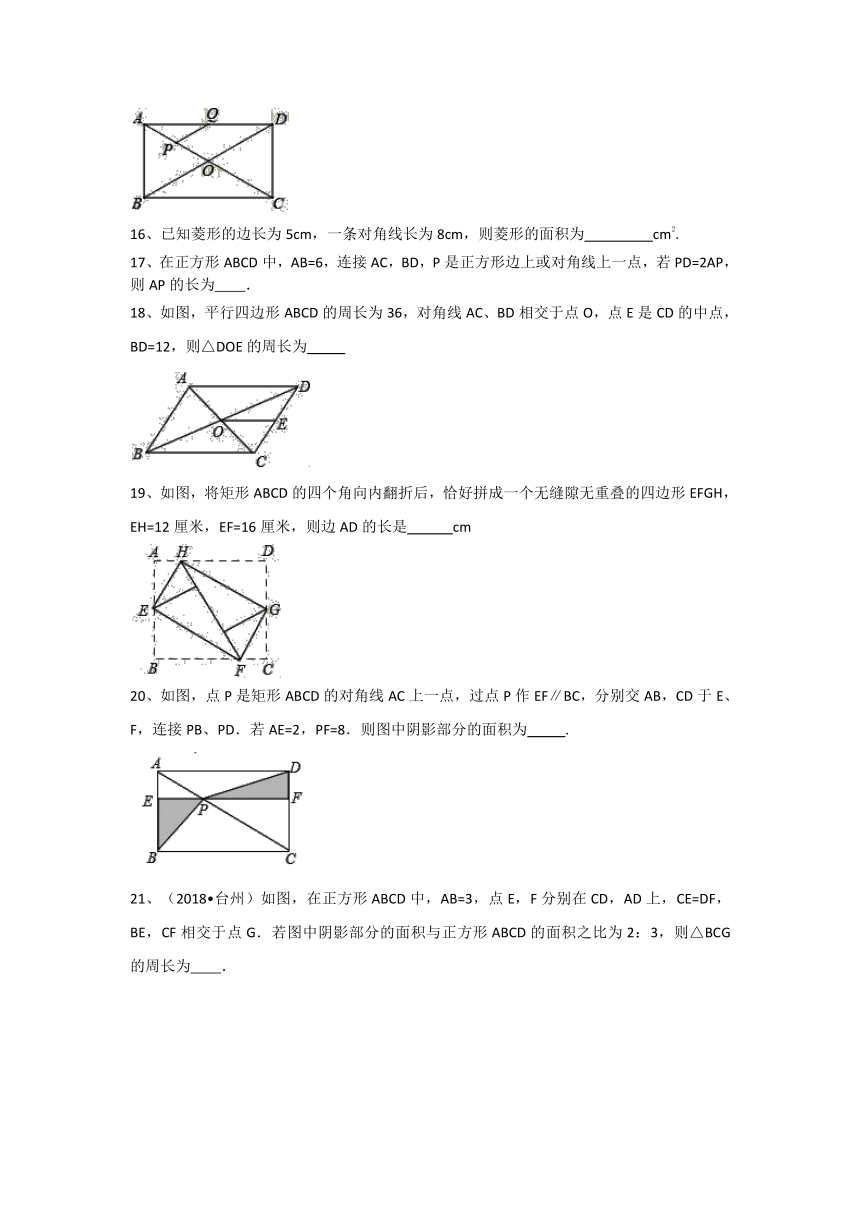
16、已知菱形的边长为5cm,一条对角线长为8cm,则菱形的面积为 cm2.
17、在正方形ABCD中,AB=6,连接AC,BD,P是正方形边上或对角线上一点,若PD=2AP,则AP的长为 .
18、如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为
19、如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是 cm
20、如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为 .
21、(2018?台州)如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为 .
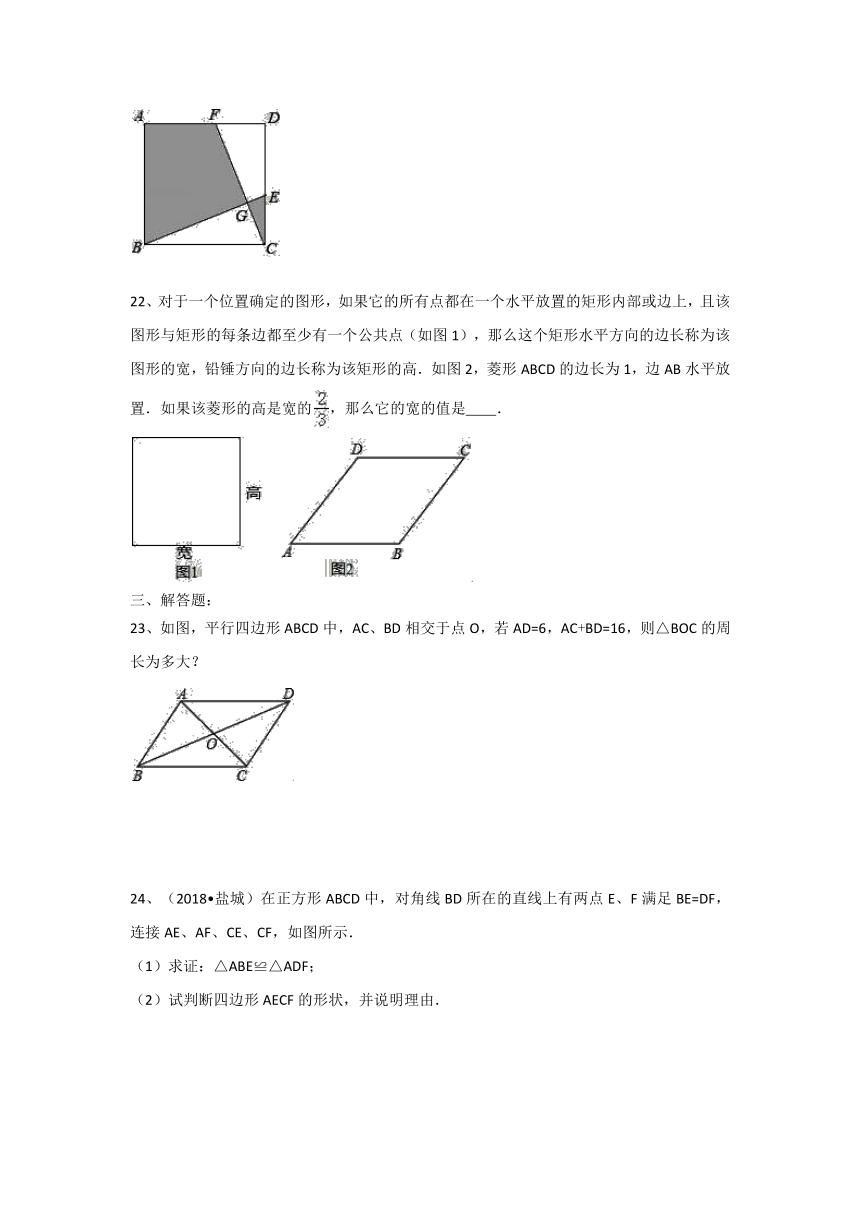
22、对于一个位置确定的图形,如果它的所有点都在一个水平放置的矩形内部或边上,且该图形与矩形的每条边都至少有一个公共点(如图1),那么这个矩形水平方向的边长称为该图形的宽,铅锤方向的边长称为该矩形的高.如图2,菱形ABCD的边长为1,边AB水平放置.如果该菱形的高是宽的,那么它的宽的值是 .
三、解答题:
23、如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为多大?
24、(2018?盐城)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
25、在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证.DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
26、已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
27、如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:
(1)∠BOD=∠C;
(2)四边形OBCD是菱形.
选择题:
1、B
2、B
3、B
4、B
5、D
6、B
7、A
8、D
9、A
10、A
11、B
12、C
二、填空题:
13、30°或150°
14、AB=BC或AC⊥BD
15、2.5
16、40
17、2或2√3或√14﹣√2
18、15
19、20
20、16
21、√15+3
22、18/13
三、解答题:
23、∵四边形ABCD是平行四边形,
∴AD=BC=6,OA=OC,OB=OD,
∵AC+BD=16,
∴OB+OC=8,
∴△BOC的周长=BC+OB+OC=6+8=14,
24、(1)∵正方形ABCD,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF,
在△ABE与△ADF中
,
∴△ABE≌△ADF(SAS);
(2)连接AC,四边形AECF是菱形.
理由:∵正方形ABCD,
∴OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
25、(1)在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
又∵AD=EA,
∴△ADF≌△EAB,
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.
26、(1)∵AE=CF,
∴AE+EF=CF+FE,即AF=CE.
又ABCD是平行四边形,
∴AD=CB,AD∥BC.
∴∠DAF=∠BCE.
在△ADF与△CBE中
,
∴△ADF≌△CBE(SAS).
(2)∵△ADF≌△CBE,
∴∠DFA=∠BEC.
∴DF∥EB.
27、(1)延长OA到E,
∵OA=OB,
∴∠ABO=∠BAO,
又∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO)
即∠BOD=2∠BAD,
又∠C=2∠BAD,
∴∠BOD=∠C;
(2)连接OC,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,∠BCO=∠DCO,
∵∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,
∴∠BOC=∠BOD,∠BCO=∠BCD,
又∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴BO=BC,
又OB=OD,BC=CD,
∴OB=BC=CD=DO,
∴四边形OBCD是菱形.
选择题:
1、下列说法中,正确个数有( )
①对顶角相等;
②两直线平行,同旁内角相等;
③对角线互相垂直的四边形为菱形;
④对角线互相垂直平分且相等的四边形为正方形.
A.1个 B.2个 C.3个 D.4个
2、已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
3、在平行四边形ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
4、如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A.50° B.40° C.30° D.20°
5、如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDF
6、如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
A.1 B. C. D.
7、如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
8、如图在平行四边形ABCD中,已知AC=4cm,若△ACD的周长为13cm,则平行四边形ABCD的周长为( )
A.26cm B.24cm C.20cm D.18cm
9、如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=θ1,∠PBA=θ2,∠PCB=θ3,∠PDC=θ4,若∠APB=80°,∠CPD=50°,则( )
A.(θ1+θ4)﹣(θ2+θ3)=30° B.(θ2+θ4)﹣(θ1+θ3)=40°
C.(θ1+θ2)﹣(θ3+θ4)=70° D.(θ1+θ2)+(θ3+θ4)=180°
10、如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A.24 B.18 C.12 D.9
11、如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
12、(2018?威海)矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1 B. C. D.
二、填空题:
13、(2018?武汉)以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .
14、如图,在平行四边形ABCD中,添加一个条件 使平行四边形ABCD是菱形.
15、如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的长度为 .
16、已知菱形的边长为5cm,一条对角线长为8cm,则菱形的面积为 cm2.
17、在正方形ABCD中,AB=6,连接AC,BD,P是正方形边上或对角线上一点,若PD=2AP,则AP的长为 .
18、如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为
19、如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是 cm
20、如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为 .
21、(2018?台州)如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为 .
22、对于一个位置确定的图形,如果它的所有点都在一个水平放置的矩形内部或边上,且该图形与矩形的每条边都至少有一个公共点(如图1),那么这个矩形水平方向的边长称为该图形的宽,铅锤方向的边长称为该矩形的高.如图2,菱形ABCD的边长为1,边AB水平放置.如果该菱形的高是宽的,那么它的宽的值是 .
三、解答题:
23、如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为多大?
24、(2018?盐城)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
25、在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证.DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
26、已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
27、如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:
(1)∠BOD=∠C;
(2)四边形OBCD是菱形.
选择题:
1、B
2、B
3、B
4、B
5、D
6、B
7、A
8、D
9、A
10、A
11、B
12、C
二、填空题:
13、30°或150°
14、AB=BC或AC⊥BD
15、2.5
16、40
17、2或2√3或√14﹣√2
18、15
19、20
20、16
21、√15+3
22、18/13
三、解答题:
23、∵四边形ABCD是平行四边形,
∴AD=BC=6,OA=OC,OB=OD,
∵AC+BD=16,
∴OB+OC=8,
∴△BOC的周长=BC+OB+OC=6+8=14,
24、(1)∵正方形ABCD,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF,
在△ABE与△ADF中
,
∴△ABE≌△ADF(SAS);
(2)连接AC,四边形AECF是菱形.
理由:∵正方形ABCD,
∴OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
25、(1)在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
又∵AD=EA,
∴△ADF≌△EAB,
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.
26、(1)∵AE=CF,
∴AE+EF=CF+FE,即AF=CE.
又ABCD是平行四边形,
∴AD=CB,AD∥BC.
∴∠DAF=∠BCE.
在△ADF与△CBE中
,
∴△ADF≌△CBE(SAS).
(2)∵△ADF≌△CBE,
∴∠DFA=∠BEC.
∴DF∥EB.
27、(1)延长OA到E,
∵OA=OB,
∴∠ABO=∠BAO,
又∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO)
即∠BOD=2∠BAD,
又∠C=2∠BAD,
∴∠BOD=∠C;
(2)连接OC,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,∠BCO=∠DCO,
∵∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,
∴∠BOC=∠BOD,∠BCO=∠BCD,
又∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴BO=BC,
又OB=OD,BC=CD,
∴OB=BC=CD=DO,
∴四边形OBCD是菱形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
