人教高中数学选修4-4 1.2.1《极坐标系的概念》课件(27ppt)
文档属性
| 名称 | 人教高中数学选修4-4 1.2.1《极坐标系的概念》课件(27ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-13 08:13:28 | ||
图片预览







文档简介
1956年,斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。
? 那时,落魄、一文不名的笛卡尔过着乞讨的生活,全部的财产只有身上穿的破破烂烂的衣服和随身所带的几本数学书籍。生性清高的笛卡尔从来不开口请求路人施舍,他只是默默地低头在纸上写写画画,潜心于他的数学世界。一个宁静的午后,笛卡尔照例坐在街头,沐浴在阳光中研究数学问题。他如此沉溺于数学世界,身边过往的人群,喧闹的车马队伍。都无法对他造成干扰。突然,有人来到他旁边,拍了拍他的肩膀,“你在干什么呢?”扭过头,笛卡尔看到一张年轻秀丽的脸庞,一双清澈的眼睛如湛蓝的湖水,楚楚动人,长长的睫毛一眨一眨的,期待着他的回应。她就是瑞典的小公主,国王最宠爱的女儿克里斯汀。
她蹲下身,拿过笛卡尔的数学书和草稿纸,和他交谈起来。言谈中,他发现,这个小女孩思维敏捷,对数学有着浓厚的兴趣。和女孩道别后,笛卡尔渐渐忘却了这件事,依旧每天坐在街头写写画画。几天后,他意外地接到通知,国王聘请他做小公主的数学老师。满心疑惑的笛卡尔跟随前来通知的侍卫一起来到皇宫,在会客厅等候的时候,他听到了从远处传来的银铃般的笑声。转过身,他看到了前儿天在街头偶遇的女孩子。慌忙中,他赶紧低头行礼。从此,他当上了公主的数学老师。
公主的数学在笛卡尔的悉心指导下突飞猛进,他们之间也开始变得亲密起来。笛卡尔向她介绍了他研究的新领域——直角坐标系。通过它,代数与几何可以结合起来,也就是日后笛卡尔创立的解析几何学的雏形。在笛卡尔的带领下,克里斯汀走进了奇妙的坐标世界,她对曲线着了迷。每天的形影不离也使他们彼此产生了爱慕之心。在瑞典这个浪漫的国度里,一段纯粹、美好的爱情悄然萌发。然而,没过多久,他们的恋情传到了国王的耳朵里。国王大怒,下令马上将笛卡尔处死。在克里斯汀的苦苦哀求下,国王将他放逐回国,公主被软禁在宫中。当时,欧洲大陆正在流行黑死病。身体孱弱的笛卡尔回到法国后不久,便染上重病。
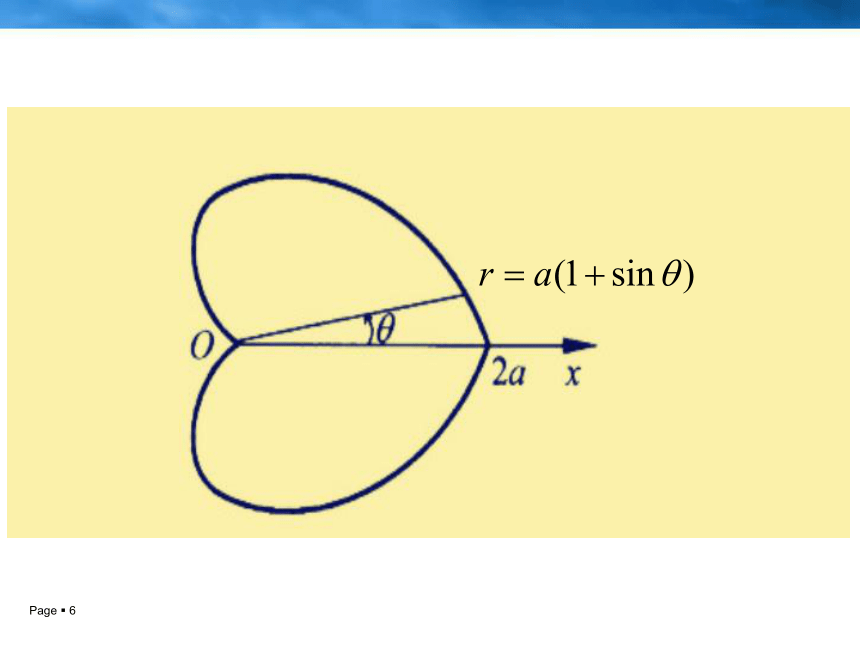
在生命进入倒计时的那段日子,他日夜思念的还是街头偶遇的那张温暖的笑脸。他每天坚持给她写信,盼望着她的回音。然而,这些信都被国王拦截下来,公主一直没有收到他的任何消息。在笛卡尔给克里斯汀寄出第十三封信后,他永远地离开了这个世界。此时,被软禁在宫中的小公主依然徘徊在皇宫的走廊里,思念着远方的情人。这最后一封信上没有写一句话,只有一个方程:r=a(1-sinθ)。国王看不懂,以为这个方程里隐藏着两个人不可告人的秘密,便把全城的数学家召集到皇宫,但是没有人能解开这个函数式。他不忍看着心爱的女儿每天闷闷不乐,便把这封信给了她。
拿到信的克里斯汀欣喜若狂,她立即明白了恋人的意图,找来纸和笔,着手把方程图形画了出来,一颗心形图案出现在眼前,克里斯汀不禁流下感动的泪水,这条曲线就是著名的“心形线”。国王去世后,克里斯汀继承王位,登基后,她便立刻派人去法国寻找心上人的下落,收到的却是笛卡尔去世的消息,留下了一个永远的遗憾……这封享誉世界的另类情书,至今,还保存在欧洲笛卡尔的纪念馆里。
事实上,笛卡尔和克里斯蒂娜的确有过交情。不过,笛卡尔是 1649 年 10 月 4 日应克里斯蒂娜邀请才来到的瑞典,并且当时克里斯蒂娜已经成为了瑞典女王。并且,笛卡尔与克里斯蒂娜谈论的主要是哲学问题。有资料记载,由于克里斯蒂娜女王时间安排很紧,笛卡尔只能在早晨五点与她探讨哲学。天气寒冷加上过度操劳让笛卡尔不幸患上肺炎,这才是笛卡尔真正的死因。
心形线的故事究竟几分是真几分是假,还是留给大家自己判断吧。
极坐标系的概念
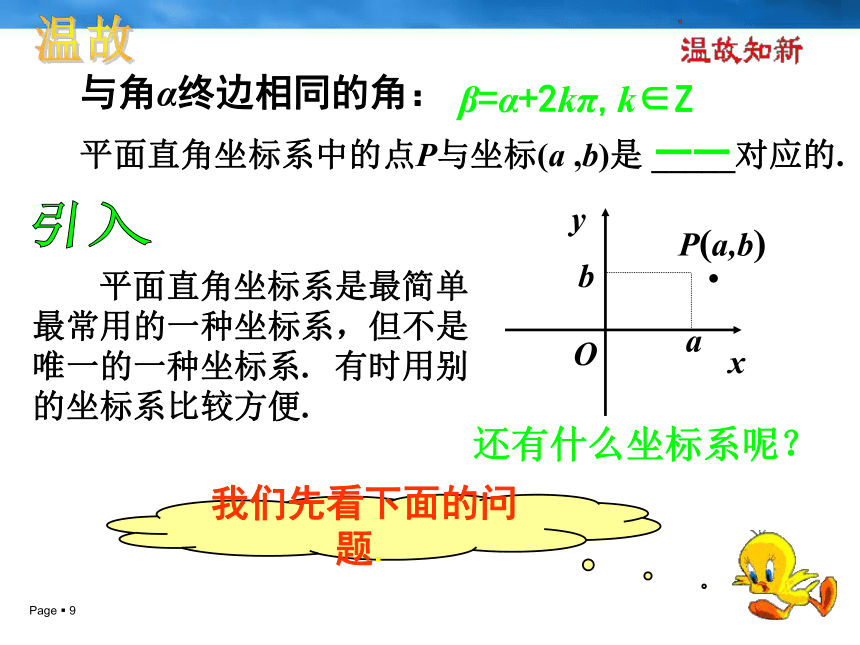
平面直角坐标系中的点P与坐标(a ,b)是 _____对应的.
平面直角坐标系是最简单最常用的一种坐标系,但不是唯一的一种坐标系. 有时用别的坐标系比较方便.
我们先看下面的问题.
还有什么坐标系呢?
与角α终边相同的角:
β=α+2kπ,k∈Z
一一
5 海里
(1)距离:5 海里
(2)方向:东偏北20?.
O
x
拯救船
20?
发现走私!!!
如何确定以下两船的位置关系呢?
距离40 km
以天河路为X轴
以广州大道为Y轴...
请问:
去广州塔怎么走?
以天河路为X轴
以广州大道为Y轴...
从这向东
2000米。
请问:
去广州塔怎么走?
从这向东
走2000米.
请问:去广州塔怎么走?
思考:“从这向南走2000米”这句话包含哪些要素?
它为何能使问路人明确屠宰场的位置?
请分析这句话,他告诉了问路人什么?
从这向东走2000米!
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。
1、极坐标系的建立:
在平面内取一个定点O,叫做极点;
自极点O引一条射线OX,叫做极轴;
再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).
这样就建立了一个极坐标系.
O
建构数学
2、极坐标系内一点的极坐标的规定
对于平面上任意一点M,用?表示线段OM的长度,用?表示以射线OX为始边,射线OM为终边所成的角,?叫做点M的极径, ?叫做点M的极角,有序数对(?,?)就叫做M的极坐标。
极点的极坐标为____________________
(0, ?), ?可为任意值.
思考: 对比直角坐标系,比较异同。
要素:____________________
____________________;
(2) 平面内点的极坐标用_____表示.
极点、极轴、长度单位、
计算角度的正方向
(?, ?)
例1、 如图,写出各点的极坐标:
x
?
1
数学运用
[变式训练 ] 在图1-11上描下列点:
[小结]由极坐标描点的步骤:
(1) 先按极角找到点所在射线;
(2) 在此射线上按极径描点.
思考:
①平面上一点的极坐标是否唯一?
若不唯一,那有多少种表示方法?
②不同的极坐标是否可以写出统一表达式?
3、点的极坐标的表达式的研究
请说出点M的极坐标的表达式?
思考:这些极坐标之间有何异同?
思考:这些极角有何关系?
这些极角的始边相同,终边也相同。也就是说它们是终边相同的角。
极径相同,不同的是极角.
4、极坐标系下点与它的极坐标的对应情况
[1]给定(?,?),就可以在极坐标平面内确定唯一的一点M
[2]给定平面上一点M,但却有无数个极坐标与之对应。
原因在于:极角有无数个。
如果限定ρ>0,0≤θ<2π
那么除极点外,平面内的点和极坐标就可以一一对应了.
数学运用
? 在一般情况下,极径都是取正值。但在某些必要的
情况下,也允许取负值(?<0):
当?<0时如何规定(?, ?)对应的点的位置?
当?<0时,点M(?, ?)的位置规定:
?
M
(?, ?)
点M:在角?终边的反向延长线上,且|OM|=|?|
5、关于负极径
小结: 从比较来看, 负极径比正极径多了一个操作, 将射线OP“反向延长”.
x
?
[小结]
(?, ?)
(?, 2k?+?)
(-?, ?+?)
(-?, ?+(2k+1)?)
都是同一点的
极坐标.
1
[3]一点的极坐标有否统一的表达式?
[1]建立一个极坐标系需要哪些要素?
极点;极轴;长度单位;计算角度的正方向.
[2]极坐标系内一点的极坐标有多少种表达式?
无数,极角有无数个.
有。(ρ,2kπ+θ)
课堂小结
课后作业
? 那时,落魄、一文不名的笛卡尔过着乞讨的生活,全部的财产只有身上穿的破破烂烂的衣服和随身所带的几本数学书籍。生性清高的笛卡尔从来不开口请求路人施舍,他只是默默地低头在纸上写写画画,潜心于他的数学世界。一个宁静的午后,笛卡尔照例坐在街头,沐浴在阳光中研究数学问题。他如此沉溺于数学世界,身边过往的人群,喧闹的车马队伍。都无法对他造成干扰。突然,有人来到他旁边,拍了拍他的肩膀,“你在干什么呢?”扭过头,笛卡尔看到一张年轻秀丽的脸庞,一双清澈的眼睛如湛蓝的湖水,楚楚动人,长长的睫毛一眨一眨的,期待着他的回应。她就是瑞典的小公主,国王最宠爱的女儿克里斯汀。
她蹲下身,拿过笛卡尔的数学书和草稿纸,和他交谈起来。言谈中,他发现,这个小女孩思维敏捷,对数学有着浓厚的兴趣。和女孩道别后,笛卡尔渐渐忘却了这件事,依旧每天坐在街头写写画画。几天后,他意外地接到通知,国王聘请他做小公主的数学老师。满心疑惑的笛卡尔跟随前来通知的侍卫一起来到皇宫,在会客厅等候的时候,他听到了从远处传来的银铃般的笑声。转过身,他看到了前儿天在街头偶遇的女孩子。慌忙中,他赶紧低头行礼。从此,他当上了公主的数学老师。
公主的数学在笛卡尔的悉心指导下突飞猛进,他们之间也开始变得亲密起来。笛卡尔向她介绍了他研究的新领域——直角坐标系。通过它,代数与几何可以结合起来,也就是日后笛卡尔创立的解析几何学的雏形。在笛卡尔的带领下,克里斯汀走进了奇妙的坐标世界,她对曲线着了迷。每天的形影不离也使他们彼此产生了爱慕之心。在瑞典这个浪漫的国度里,一段纯粹、美好的爱情悄然萌发。然而,没过多久,他们的恋情传到了国王的耳朵里。国王大怒,下令马上将笛卡尔处死。在克里斯汀的苦苦哀求下,国王将他放逐回国,公主被软禁在宫中。当时,欧洲大陆正在流行黑死病。身体孱弱的笛卡尔回到法国后不久,便染上重病。
在生命进入倒计时的那段日子,他日夜思念的还是街头偶遇的那张温暖的笑脸。他每天坚持给她写信,盼望着她的回音。然而,这些信都被国王拦截下来,公主一直没有收到他的任何消息。在笛卡尔给克里斯汀寄出第十三封信后,他永远地离开了这个世界。此时,被软禁在宫中的小公主依然徘徊在皇宫的走廊里,思念着远方的情人。这最后一封信上没有写一句话,只有一个方程:r=a(1-sinθ)。国王看不懂,以为这个方程里隐藏着两个人不可告人的秘密,便把全城的数学家召集到皇宫,但是没有人能解开这个函数式。他不忍看着心爱的女儿每天闷闷不乐,便把这封信给了她。
拿到信的克里斯汀欣喜若狂,她立即明白了恋人的意图,找来纸和笔,着手把方程图形画了出来,一颗心形图案出现在眼前,克里斯汀不禁流下感动的泪水,这条曲线就是著名的“心形线”。国王去世后,克里斯汀继承王位,登基后,她便立刻派人去法国寻找心上人的下落,收到的却是笛卡尔去世的消息,留下了一个永远的遗憾……这封享誉世界的另类情书,至今,还保存在欧洲笛卡尔的纪念馆里。
事实上,笛卡尔和克里斯蒂娜的确有过交情。不过,笛卡尔是 1649 年 10 月 4 日应克里斯蒂娜邀请才来到的瑞典,并且当时克里斯蒂娜已经成为了瑞典女王。并且,笛卡尔与克里斯蒂娜谈论的主要是哲学问题。有资料记载,由于克里斯蒂娜女王时间安排很紧,笛卡尔只能在早晨五点与她探讨哲学。天气寒冷加上过度操劳让笛卡尔不幸患上肺炎,这才是笛卡尔真正的死因。
心形线的故事究竟几分是真几分是假,还是留给大家自己判断吧。
极坐标系的概念
平面直角坐标系中的点P与坐标(a ,b)是 _____对应的.
平面直角坐标系是最简单最常用的一种坐标系,但不是唯一的一种坐标系. 有时用别的坐标系比较方便.
我们先看下面的问题.
还有什么坐标系呢?
与角α终边相同的角:
β=α+2kπ,k∈Z
一一
5 海里
(1)距离:5 海里
(2)方向:东偏北20?.
O
x
拯救船
20?
发现走私!!!
如何确定以下两船的位置关系呢?
距离40 km
以天河路为X轴
以广州大道为Y轴...
请问:
去广州塔怎么走?
以天河路为X轴
以广州大道为Y轴...
从这向东
2000米。
请问:
去广州塔怎么走?
从这向东
走2000米.
请问:去广州塔怎么走?
思考:“从这向南走2000米”这句话包含哪些要素?
它为何能使问路人明确屠宰场的位置?
请分析这句话,他告诉了问路人什么?
从这向东走2000米!
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。
1、极坐标系的建立:
在平面内取一个定点O,叫做极点;
自极点O引一条射线OX,叫做极轴;
再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).
这样就建立了一个极坐标系.
O
建构数学
2、极坐标系内一点的极坐标的规定
对于平面上任意一点M,用?表示线段OM的长度,用?表示以射线OX为始边,射线OM为终边所成的角,?叫做点M的极径, ?叫做点M的极角,有序数对(?,?)就叫做M的极坐标。
极点的极坐标为____________________
(0, ?), ?可为任意值.
思考: 对比直角坐标系,比较异同。
要素:____________________
____________________;
(2) 平面内点的极坐标用_____表示.
极点、极轴、长度单位、
计算角度的正方向
(?, ?)
例1、 如图,写出各点的极坐标:
x
?
1
数学运用
[变式训练 ] 在图1-11上描下列点:
[小结]由极坐标描点的步骤:
(1) 先按极角找到点所在射线;
(2) 在此射线上按极径描点.
思考:
①平面上一点的极坐标是否唯一?
若不唯一,那有多少种表示方法?
②不同的极坐标是否可以写出统一表达式?
3、点的极坐标的表达式的研究
请说出点M的极坐标的表达式?
思考:这些极坐标之间有何异同?
思考:这些极角有何关系?
这些极角的始边相同,终边也相同。也就是说它们是终边相同的角。
极径相同,不同的是极角.
4、极坐标系下点与它的极坐标的对应情况
[1]给定(?,?),就可以在极坐标平面内确定唯一的一点M
[2]给定平面上一点M,但却有无数个极坐标与之对应。
原因在于:极角有无数个。
如果限定ρ>0,0≤θ<2π
那么除极点外,平面内的点和极坐标就可以一一对应了.
数学运用
? 在一般情况下,极径都是取正值。但在某些必要的
情况下,也允许取负值(?<0):
当?<0时如何规定(?, ?)对应的点的位置?
当?<0时,点M(?, ?)的位置规定:
?
M
(?, ?)
点M:在角?终边的反向延长线上,且|OM|=|?|
5、关于负极径
小结: 从比较来看, 负极径比正极径多了一个操作, 将射线OP“反向延长”.
x
?
[小结]
(?, ?)
(?, 2k?+?)
(-?, ?+?)
(-?, ?+(2k+1)?)
都是同一点的
极坐标.
1
[3]一点的极坐标有否统一的表达式?
[1]建立一个极坐标系需要哪些要素?
极点;极轴;长度单位;计算角度的正方向.
[2]极坐标系内一点的极坐标有多少种表达式?
无数,极角有无数个.
有。(ρ,2kπ+θ)
课堂小结
课后作业
