2.1 数列的概念与简单表示 课件(35张PPT)
文档属性
| 名称 | 2.1 数列的概念与简单表示 课件(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-13 16:48:52 | ||
图片预览







文档简介
§2.1数列的概念
与简单表示法
3. ?1的正整数次幂:?1, 1, ?1, 1, …
2. 正整数的倒数
L
5
1
,
4
1
,
3
1
,
2
1
,
1
1. 由小到大的正偶数排成一列
2,4,6,8,?
观察
§2.1数列的概念与简单表示法
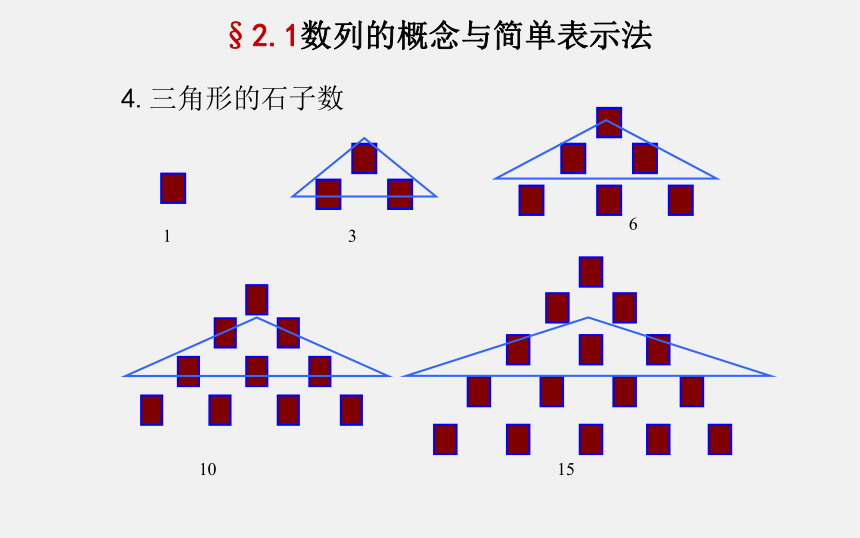
4.三角形的石子数
1
3
6
10
15
§2.1数列的概念与简单表示法
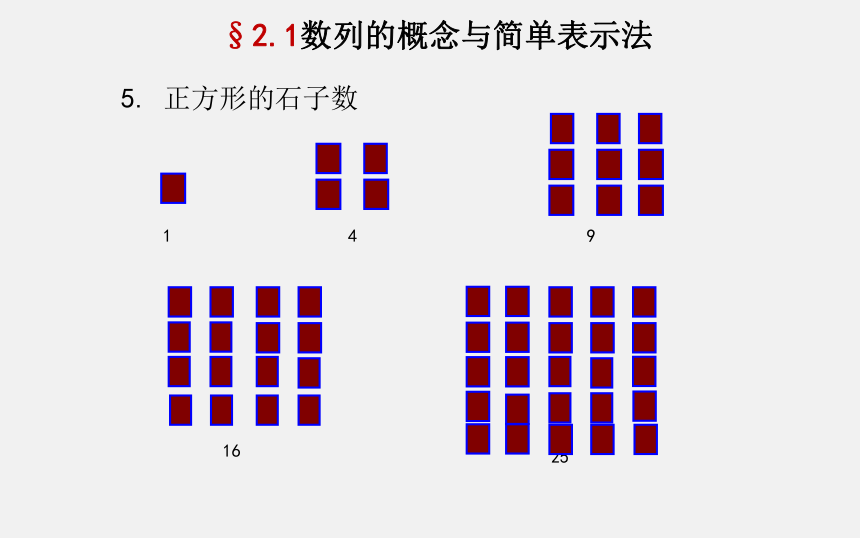
5. 正方形的石子数
1
4
9
16
25
§2.1数列的概念与简单表示法
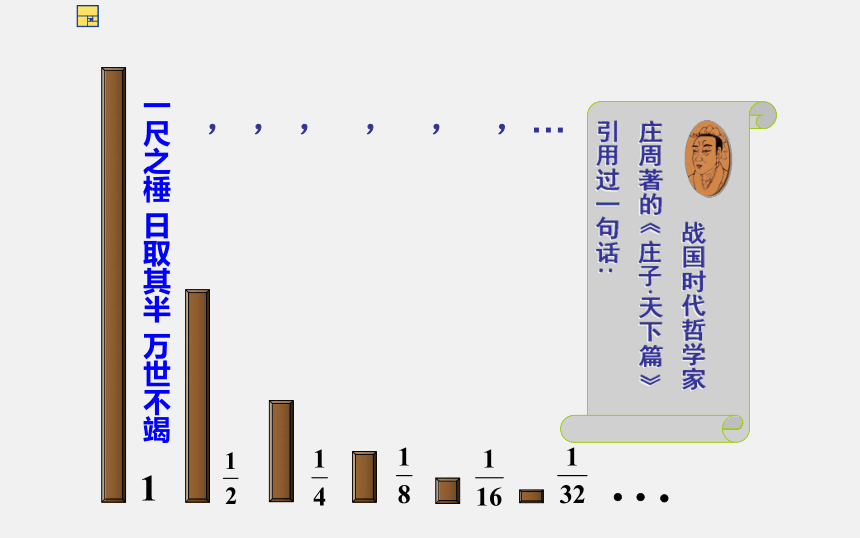
战国时代哲学家庄周著的《庄子·天下篇》引用过一句话:
, , , , , ,…
一尺之棰 日取其半 万世不竭
7.如图表示堆放的钢管,共堆放了6层.自上而下各层的钢管数排列成一列数:
5,6,7,8,9,10
§2.1数列的概念与简单表示法
按照一定顺序排列的一列数称为数列. 数列中的每一个数叫做这个数列的项,各项依次叫做这个数列的第一项(或首项), 第二项, … ,第n项, …..
定义
数列的第n项an叫做数列的通项(或一般项).
数列的一般形式
或:a1,a2,a3,?
数列的定义
问:下面二个列数是否为同一数列?
1,2,3,4,5
2,1,3,4,5
结论:因其排列次序不同,故不是同一数列.
定义的辨析
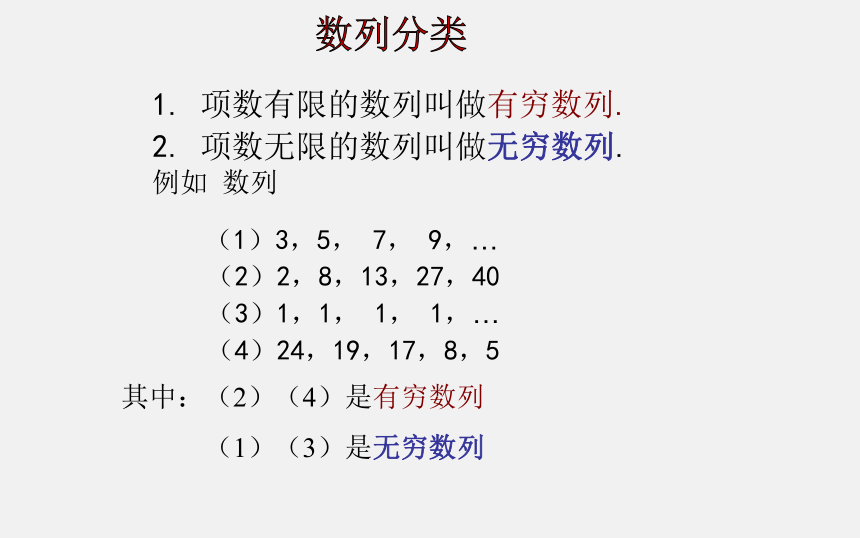
1. 项数有限的数列叫做有穷数列.
2. 项数无限的数列叫做无穷数列.
(1)3,5, 7, 9,…
(2)2,8,13,27,40
(3)1,1, 1, 1,…
(4)24,19,17,8,5
例如 数列
其中:(2)(4)是有穷数列
(1)(3)是无穷数列
数列分类
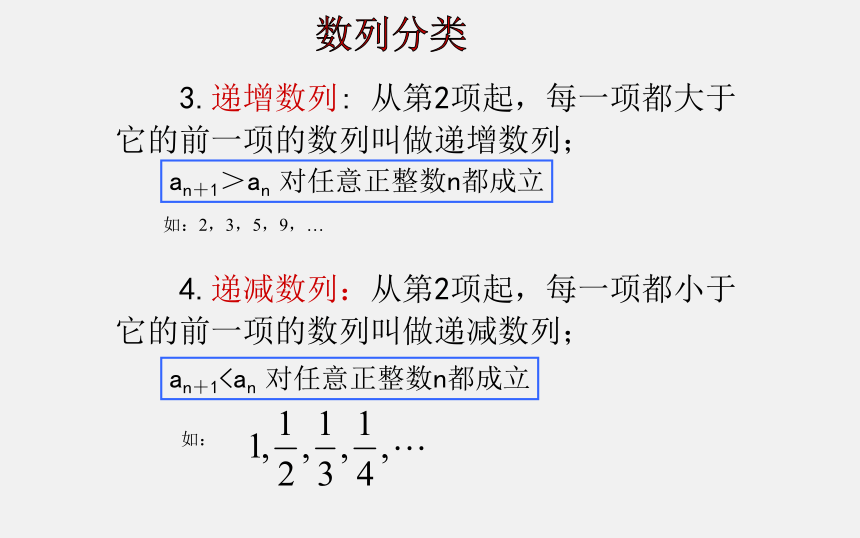
3.递增数列: 从第2项起,每一项都大于它的前一项的数列叫做递增数列;
4.递减数列:从第2项起,每一项都小于它的前一项的数列叫做递减数列;
如:2,3,5,9,?
如:
an+1>an 对任意正整数n都成立
an+1数列分类
5.常数数列:各项都相等的数列;
6.摆动数列:各从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列叫做摆动数列.
如:1,1,1,1,?(各项都是1)
如:
2,3,2,3,?
an+1= an,对任意的正整数n都成立.
数列分类
观察
下面的数列,哪些是递增数列、递减数列、常数数列、摆动数列?
(1)全体自然数构成数列
0,1,2,3,?
(2)1996?2002年某市普通高中人数(单位:万人)构成数列
82,93,105,119,129,130,132
(3)无穷多个4构成数列
4,4,4,4,?
数列分类练习
(4)目前普通的人民币面额按从大到小的顺序构成数列(单位,元)
100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01
(5)-1的1次幂,2次幂,3次幂,4次幂?构成数列
-1,1,-1,1,?
(6) 精确到1,0.1,0.01,0.001,?的不足近似值构成数列
1,1.4,1.41,1.414,?
?
数列分类练习
分析:数列 4,5,6,7,8,…
数列的项:4 5 6 7 8 …
序号: 1 2 3 4 5 …
y=x+3 定义域:N*
x
y
数列可以看成以正整数集N*(或它的有限子集{1,2,?,n})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.
数列与函数
?
对于函数y=f(x),如果f(i)(i=1,2,3,?,n,? )有意义,那么我们可以得到一个数列
f(1),f(2),f(3),?f(n),? .
数列与函数
如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式. 我们可以根据数列的通项公式写出数列.
n=1,2,3,?
思考?
通项公式可以看成数列的函数解析式,利用一个数列的通项公式,你能确定这个数列哪方面的性质?
数列通项公式
例1 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)2,4,6,8,…
(3)1,2,4 ,8 ,…
(6)2,6,12,20,…
(2)1,3,5,7,…
(4)
(5)9,99,999,9999,…
?
?
?
?
?
?
归纳数列通项公式
(1)
(2)
练习1 根据数列{an}的通项公式,写出它的前5项:
解:(1)在通项公式中依次取n=1,2,3,4,5,得到数列 的前5项为
(2)在通项公式中依次取n=1,2,3,4,5,得么数列 的前5项为
-1,2,-3,4, -5.
课堂练习
练习2 写出下面数列的一个通项公式,使它的前4 项分别是下列各数:
(1) 1,0,1,0,…
(2)
?
?
课堂练习
关于通项公式
通项公式的优点:
①简明、全面地概括了项数与项的关系;
②可以通过通项公式求出任意项的值.
1.不是每一个数列都能写出其通项公式(如数列3)
2.数列的通项公式不唯一 如: ?1,1,?1,1,…
特别说明
数列的表示
1. 通项公式 an=f(n)
2. 列表
或写成{n2}
3. 图象
数列的图象是一系列孤立的点(n,an)
n 1 2 3 ?
an a1 a2 a3 ?
优点:不需要计算就可以直接看出与项相对应的关系
列表法:
图象法
优点:能直接形象地表示出随着项数的变化,相应项变化的趋势,直观明了.
数列的表示
例2. 如图三角形称为谢宾斯基(Sierpinski)三角形.在下图四个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象.
谢宾斯基三角形
解: 如图,这四个三角形中着色三角形的个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.所以,这个数列的一个通项公式是
在直角坐标系中的图象见后图.
谢宾斯基三角形
谢宾斯基三角形
小 结
1.数列的定义;
2.数列的通项公式;
3.数列和函数的关系;
4.数列的表示
5.数列的递推公式
作业
练习P31 4
习题P33 A组:4、5、6 B组:1
谢谢观赏
Thanks!
§2.1数列的概念与简单表示法
斐波那契数列简介
“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1250年.籍贯大概是比萨).他被人称作“比萨的列昂纳多”.1202年,他撰写了《算盘全书》(Liber Abacci)一书.他是第一个研究了印度和阿拉伯数学理论的欧洲人.他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学.他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学.
斐波那契数列(又译作“斐波拉契数列”或“斐波那切数列”)是一个非常美丽、和谐的数列,它的形状可以用排成螺旋状的一系列正方形来说明(如上图),起始的正方形(图中用灰色表示)的边长为1,在它左边的那个正方形的边长也是1 ,在这两个正方形的上方再放一个正方形,其边长为2,以后顺次加上边长为3、5、8、13、21……等等的正方形.这些数字每一个都等于前面两个数之和,它们正好构成了斐波那契数列.
斐波那契数列
斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”.
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来.如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
我们不妨拿新出生的一对小兔子分析一下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔后,兔子数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对;
“兔子数列”
依次类推可以列出下表:
经过月数:0 1 2 3 4 5 6 7 8 9 10 11
兔子对数:1 1 2 3 5 8 13 21 34 55 89 144
表中数字1,1,2,3,5,8---构成了一个数列.这个数列有个十分明显的特点,那是:前面相邻两项之和,构成了后一项.
斐波那契(Fibonacci)数列的递推关系式:
f(1)=1
f(2)=1
f(n)=f(n-1)+f(n-2),其中n?2
{f(n)}即为斐波那契数列.
斐波那契数列的特征:从第三项起每一项等于它相邻的前2项的和.
斐波那契数列
斐波那契数列举例
1.多米诺牌(可以看作一个2×1大小的方格)完全覆盖一个n×2的棋盘,覆盖的方案数等于斐波那契数列.
2.从蜜蜂的繁殖来看,雄蜂只有母亲,没有父亲,因为蜂后产的卵,受精的孵化为雌蜂,未受精的孵化为雄峰.人们在追溯雄峰的祖先时,发现一只雄峰的第n代祖先的数目刚好就是斐波那契数列的第n项F(n).
3.钢琴的13个半音阶的排列完全与雄蜂第六代的排列情况类似,说明音调也与斐波那契数列有关.
5.自然界中一些花朵的花瓣数目符合于斐波那契数列,也就是说在大多数情况下,一朵花花瓣的数目都是3,5,8,13,21,34,……(有6枚是两套3枚;有4枚可能是基因突变).
4.如果一根树枝每年长出一根新枝,而长出的新枝两年以后,每年也长出一根新枝,那么历年的树枝数,也构成一个斐波拉契数列 .
斐波那契数列举例
与简单表示法
3. ?1的正整数次幂:?1, 1, ?1, 1, …
2. 正整数的倒数
L
5
1
,
4
1
,
3
1
,
2
1
,
1
1. 由小到大的正偶数排成一列
2,4,6,8,?
观察
§2.1数列的概念与简单表示法
4.三角形的石子数
1
3
6
10
15
§2.1数列的概念与简单表示法
5. 正方形的石子数
1
4
9
16
25
§2.1数列的概念与简单表示法
战国时代哲学家庄周著的《庄子·天下篇》引用过一句话:
, , , , , ,…
一尺之棰 日取其半 万世不竭
7.如图表示堆放的钢管,共堆放了6层.自上而下各层的钢管数排列成一列数:
5,6,7,8,9,10
§2.1数列的概念与简单表示法
按照一定顺序排列的一列数称为数列. 数列中的每一个数叫做这个数列的项,各项依次叫做这个数列的第一项(或首项), 第二项, … ,第n项, …..
定义
数列的第n项an叫做数列的通项(或一般项).
数列的一般形式
或:a1,a2,a3,?
数列的定义
问:下面二个列数是否为同一数列?
1,2,3,4,5
2,1,3,4,5
结论:因其排列次序不同,故不是同一数列.
定义的辨析
1. 项数有限的数列叫做有穷数列.
2. 项数无限的数列叫做无穷数列.
(1)3,5, 7, 9,…
(2)2,8,13,27,40
(3)1,1, 1, 1,…
(4)24,19,17,8,5
例如 数列
其中:(2)(4)是有穷数列
(1)(3)是无穷数列
数列分类
3.递增数列: 从第2项起,每一项都大于它的前一项的数列叫做递增数列;
4.递减数列:从第2项起,每一项都小于它的前一项的数列叫做递减数列;
如:2,3,5,9,?
如:
an+1>an 对任意正整数n都成立
an+1
5.常数数列:各项都相等的数列;
6.摆动数列:各从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列叫做摆动数列.
如:1,1,1,1,?(各项都是1)
如:
2,3,2,3,?
an+1= an,对任意的正整数n都成立.
数列分类
观察
下面的数列,哪些是递增数列、递减数列、常数数列、摆动数列?
(1)全体自然数构成数列
0,1,2,3,?
(2)1996?2002年某市普通高中人数(单位:万人)构成数列
82,93,105,119,129,130,132
(3)无穷多个4构成数列
4,4,4,4,?
数列分类练习
(4)目前普通的人民币面额按从大到小的顺序构成数列(单位,元)
100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01
(5)-1的1次幂,2次幂,3次幂,4次幂?构成数列
-1,1,-1,1,?
(6) 精确到1,0.1,0.01,0.001,?的不足近似值构成数列
1,1.4,1.41,1.414,?
?
数列分类练习
分析:数列 4,5,6,7,8,…
数列的项:4 5 6 7 8 …
序号: 1 2 3 4 5 …
y=x+3 定义域:N*
x
y
数列可以看成以正整数集N*(或它的有限子集{1,2,?,n})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.
数列与函数
?
对于函数y=f(x),如果f(i)(i=1,2,3,?,n,? )有意义,那么我们可以得到一个数列
f(1),f(2),f(3),?f(n),? .
数列与函数
如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式. 我们可以根据数列的通项公式写出数列.
n=1,2,3,?
思考?
通项公式可以看成数列的函数解析式,利用一个数列的通项公式,你能确定这个数列哪方面的性质?
数列通项公式
例1 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)2,4,6,8,…
(3)1,2,4 ,8 ,…
(6)2,6,12,20,…
(2)1,3,5,7,…
(4)
(5)9,99,999,9999,…
?
?
?
?
?
?
归纳数列通项公式
(1)
(2)
练习1 根据数列{an}的通项公式,写出它的前5项:
解:(1)在通项公式中依次取n=1,2,3,4,5,得到数列 的前5项为
(2)在通项公式中依次取n=1,2,3,4,5,得么数列 的前5项为
-1,2,-3,4, -5.
课堂练习
练习2 写出下面数列的一个通项公式,使它的前4 项分别是下列各数:
(1) 1,0,1,0,…
(2)
?
?
课堂练习
关于通项公式
通项公式的优点:
①简明、全面地概括了项数与项的关系;
②可以通过通项公式求出任意项的值.
1.不是每一个数列都能写出其通项公式(如数列3)
2.数列的通项公式不唯一 如: ?1,1,?1,1,…
特别说明
数列的表示
1. 通项公式 an=f(n)
2. 列表
或写成{n2}
3. 图象
数列的图象是一系列孤立的点(n,an)
n 1 2 3 ?
an a1 a2 a3 ?
优点:不需要计算就可以直接看出与项相对应的关系
列表法:
图象法
优点:能直接形象地表示出随着项数的变化,相应项变化的趋势,直观明了.
数列的表示
例2. 如图三角形称为谢宾斯基(Sierpinski)三角形.在下图四个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象.
谢宾斯基三角形
解: 如图,这四个三角形中着色三角形的个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.所以,这个数列的一个通项公式是
在直角坐标系中的图象见后图.
谢宾斯基三角形
谢宾斯基三角形
小 结
1.数列的定义;
2.数列的通项公式;
3.数列和函数的关系;
4.数列的表示
5.数列的递推公式
作业
练习P31 4
习题P33 A组:4、5、6 B组:1
谢谢观赏
Thanks!
§2.1数列的概念与简单表示法
斐波那契数列简介
“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1250年.籍贯大概是比萨).他被人称作“比萨的列昂纳多”.1202年,他撰写了《算盘全书》(Liber Abacci)一书.他是第一个研究了印度和阿拉伯数学理论的欧洲人.他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学.他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学.
斐波那契数列(又译作“斐波拉契数列”或“斐波那切数列”)是一个非常美丽、和谐的数列,它的形状可以用排成螺旋状的一系列正方形来说明(如上图),起始的正方形(图中用灰色表示)的边长为1,在它左边的那个正方形的边长也是1 ,在这两个正方形的上方再放一个正方形,其边长为2,以后顺次加上边长为3、5、8、13、21……等等的正方形.这些数字每一个都等于前面两个数之和,它们正好构成了斐波那契数列.
斐波那契数列
斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”.
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来.如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
我们不妨拿新出生的一对小兔子分析一下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔后,兔子数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对;
“兔子数列”
依次类推可以列出下表:
经过月数:0 1 2 3 4 5 6 7 8 9 10 11
兔子对数:1 1 2 3 5 8 13 21 34 55 89 144
表中数字1,1,2,3,5,8---构成了一个数列.这个数列有个十分明显的特点,那是:前面相邻两项之和,构成了后一项.
斐波那契(Fibonacci)数列的递推关系式:
f(1)=1
f(2)=1
f(n)=f(n-1)+f(n-2),其中n?2
{f(n)}即为斐波那契数列.
斐波那契数列的特征:从第三项起每一项等于它相邻的前2项的和.
斐波那契数列
斐波那契数列举例
1.多米诺牌(可以看作一个2×1大小的方格)完全覆盖一个n×2的棋盘,覆盖的方案数等于斐波那契数列.
2.从蜜蜂的繁殖来看,雄蜂只有母亲,没有父亲,因为蜂后产的卵,受精的孵化为雌蜂,未受精的孵化为雄峰.人们在追溯雄峰的祖先时,发现一只雄峰的第n代祖先的数目刚好就是斐波那契数列的第n项F(n).
3.钢琴的13个半音阶的排列完全与雄蜂第六代的排列情况类似,说明音调也与斐波那契数列有关.
5.自然界中一些花朵的花瓣数目符合于斐波那契数列,也就是说在大多数情况下,一朵花花瓣的数目都是3,5,8,13,21,34,……(有6枚是两套3枚;有4枚可能是基因突变).
4.如果一根树枝每年长出一根新枝,而长出的新枝两年以后,每年也长出一根新枝,那么历年的树枝数,也构成一个斐波拉契数列 .
斐波那契数列举例
