第20章 数据的分析复习题---解答题(含解析)
文档属性
| 名称 | 第20章 数据的分析复习题---解答题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-14 00:00:00 | ||
图片预览




文档简介
人教版八下第20章数据的分析复习题---解答题
一.解答题(共24小题)
1.(2018?柳州)一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
2.(2018?南京)随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2200
1780
7560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
3.(2018春?凉州区期末)某次歌咏比赛,前三名选手的成绩统计如下:(单位:分)
测试项目
测试成绩
王晓丽
李真
林飞扬
唱功
98
95
80
音乐常识
80
90
100
综合知识
80
90
100
将唱功、音乐常识综合知识三项测试成绩按6:3:1的加权平均分排出冠军、亚军季军,则冠军、亚军、季军各是谁?
4.(2018春?孝义市期末)2018年4月23日是第23个世界读书日.为迎接第23个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者
推荐语
读书心得
读书讲座
甲
85
83
93
乙
92
86
86
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
(2)若“推荐语”“读书心得”“读书讲座”的成绩按2:3:5确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
5.(2018春?永康市期末)为了响应“五水共治,建设美丽永康”的号召,某小区业委会随机调查了该小区20户家庭5月份的用水量,结果如下表:
5月份用水量(吨)
5
10
11
13
15
20
户数
3
5
6
3
2
1
(1)计算这20户家庭5月份的平均用水量;
(2)若该小区有800户家庭,估计该小区5月份用水量多少吨?
6.(2018?镇江)某班50名学生的身高如下(单位:cm):
160 163 152 161 167 154 158 171 156 168
178 151 156 158 165 160 148 155 162 175
158 167 157 153 164 172 153 159 174 155
169 163 158 150 177 155 166 161 159 164
171 154 157 165 152 167 157 162 155 160
(1)小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本:161,155,174,163,152,请你计算小丽所抽取的这个样本的平均数;
(2)小丽将这50个数据按身高相差4cm分组,并制作了如下的表格:
身高
频数
频率
147.5~151.5
0.06
151.5~155.5
155.5~159.5
11
m
159.5~163.5
0.18
163.5~167.5
8
0.16
167.5~171.5
4
171.5~175.5
n
0.06
175.5~179.5
2
合计
50
1
①m= ,n= ;
②这50名学生身高的中位数落在哪个身高段内?身高在哪一段的学生数最多?
7.(2018?包头)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
8.(2018?贵阳)在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二:
69
97
96
89
98
100
99
100
95
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
92.8
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
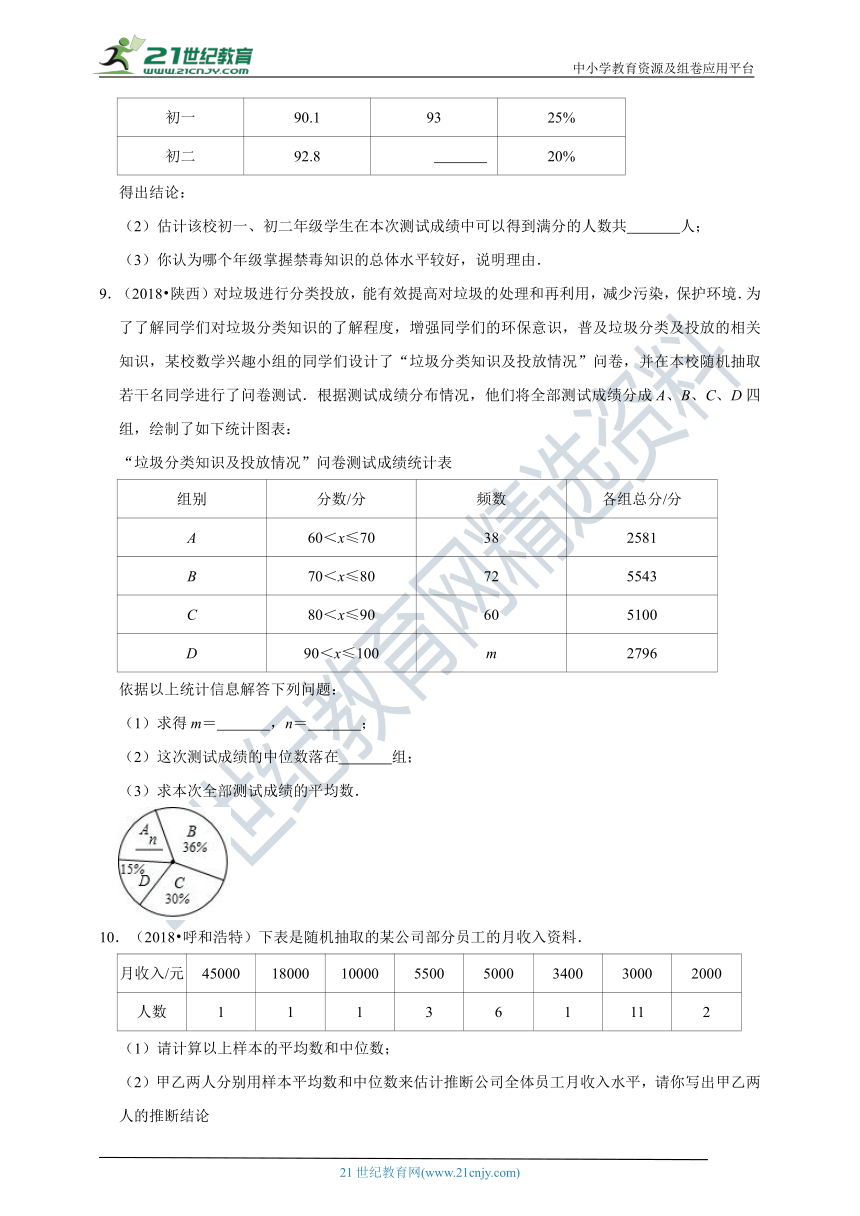
9.(2018?陕西)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
各组总分/分
A
60<x≤70
38
2581
B
70<x≤80
72
5543
C
80<x≤90
60
5100
D
90<x≤100
m
2796
依据以上统计信息解答下列问题:
(1)求得m= ,n= ;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
10.(2018?呼和浩特)下表是随机抽取的某公司部分员工的月收入资料.
月收入/元
45000
18000
10000
5500
5000
3400
3000
2000
人数
1
1
1
3
6
1
11
2
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论
;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
11.(2019?北碚区)某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整:
收集数据:从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
乙
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据:按如下分数段整理、描述这两组样本数据(请补全表格):
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
0
0
(说明:成绩80分及以上为生产技能优秀,70﹣79分为生产技能良好,60﹣69分为生产技能合格,60分以下为生产技能不合格)
分析数据:两组样本数据的平均数、中位数、众数如表所示(请补全表格):
部门
平均数
中位数
众数
甲
78.3
75
乙
78
80.5
得出结论:
(1)估计乙部门生产技能优秀的员工人数为 ;
(2)你认为 部门员工的生产技能水平较高,说明理由(至少从两个不同的角度说明推断的合理性).
12.(2019?九龙坡区)某市为提高环境质量对全市的环境污染进行综合治理,在治理的过程中环保部门随机选取了平安镇和富贵镇进行空气质量监测.
过程如下,请补充完整.
收集数据:
从2017年12月初开始连续一年对两镇的空气质量进行监测,将30天的空气污染指数(简称API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
平安镇:120 115 45 100 95 50 80 70 85 50 50 100
富贵镇:110 90 105 80 90 85 90 50 90 45 70 60
(1)整理、描述数据:
按下表整理、描述这两镇空气污染指数的数据:
空气质量为优
空气质量为良
空气质量为轻微污染
平安镇
4
6
2
富贵镇
(说明空气污染指数<50时,空气质量为优;50≤空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻度污染)
(2)分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇
平均数
中位数
众数
平安镇
80
50
富贵镇
81.3
87.5
请将以上两个表格补充完整;
(3)得出结论:可以推断出 镇这一年中环境状况比较好,理由: .(至少从两个不同的角度说明推断的合理性)
13.(2018?南通)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17
18
16
13
24
15
28
26
18
19
22
17
16
19
32
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别
一
二
三
四
五
六
七
销售额
13≤x<16
16≤x<19
19≤x<22
22≤x<25
25≤x<28
28≤x<31
31≤x<34
频数
7
9
3
a
2
b
2
数据分析表
平均数
众数
中位数
20.3
c
18
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
14.(2018?渝中区)某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
15.(2018?云南)某同学参加了学校举行的“五好小公民?红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
16.(2018?咸宁)近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
17.(2018?广州)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
18.(2019?沙坪坝区)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
组别
频数
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
6
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
b
43.1
乙车间
180
180
180
22.6
应用数据:
(1)请写出表中a= ,b= mm;
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
19.(2019?渝中区)某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分)
整理,分析过程如下:
成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
0
1
4
5
0
0
乙
1
1
4
2
1
1
(1)两组数据的极差、平均数、中位数、众数、方差如下表所示,请补充完整:
学生
极差
平均数
中位数
众数
方差
甲
83.7
86
13.21
乙
24
83.7
82
46.21
(2)若从甲、乙两人中选择一人参加知识竞赛,你会选 (填“甲“或“乙“),理由为 .
20.(2018?荆州)为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
19.2
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
21.(2018?吉林)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况,质检员进行了抽样调查,过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:g)如下:
甲:400,400,408,406,410,409,400,393,394,395
乙:403,404,396,399,402,402,405,397,402,398
整理数据:
表一
质量(g)
频数
种类
393≤x<396
396≤x<399
399≤x<402
402≤x<405
405≤x<408
408≤x<411
甲
3
0
0
1
3
乙
0
1
5
0
分析数据:
表二
种类
平均数
中位数
众数
方差
甲
401.5
400
36.85
乙
400.8
402
8.56
得出结论:
包装机分装情况比较好的是 (填甲或乙),说明你的理由.
22.(2018?舟山)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
b
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
180
22.6
应用数据:
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
23.(2018?江西)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min)
0≤x<40
40≤x<80
80≤x<120
120≤x<160
等级
D
C
B
A
人数
3
8
分析数据:补全下列表格中的统计量:
平均数
中位数
众数
80
得出结论:
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
24.(2018?威海)为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
人教版八下第20章数据的分析复习题---解答题
参考答案与试题解析
一.解答题(共24小题)
1.(2018?柳州)一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
【分析】平均数是指在一组数据中所有数据之和再除以数据的个数.
【解答】解:该同学这五次投实心球的平均成绩为:
=10.4.
故该同学这五次投实心球的平均成绩为10.4m.
2.(2018?南京)随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2200
1780
7560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
【分析】(1)根据平均数的定义计算可得;
(2)从极端值对平均数的影响作出判断,可用该店本周一到周日的日均营业额估计当月营业额.
【解答】解:(1)该店本周的日平均营业额为7560÷7=1080元;
(2)因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额,
所以去掉周六、日的营业额对平均数的影响较大,
故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合理,
方案:用该店本周一到周日的日均营业额估计当月营业额,
当月的营业额为30×1080=32400元.
3.(2018春?凉州区期末)某次歌咏比赛,前三名选手的成绩统计如下:(单位:分)
测试项目
测试成绩
王晓丽
李真
林飞扬
唱功
98
95
80
音乐常识
80
90
100
综合知识
80
90
100
将唱功、音乐常识综合知识三项测试成绩按6:3:1的加权平均分排出冠军、亚军季军,则冠军、亚军、季军各是谁?
【分析】根据加权平均数的计算公式先分别求出三个人的最后得分,再进行比较即可.
【解答】解:王晓丽的成绩是:(98×6+80×3+80)÷10=90.8(分);
李真:(95×6+90×3+90)÷10=93(分);
林飞杨:(80×6+100×3+100)÷10=88(分).
∵93>90.8>88,
∴冠军是李真、亚军是王晓丽、季军是林飞杨.
4.(2018春?孝义市期末)2018年4月23日是第23个世界读书日.为迎接第23个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者
推荐语
读书心得
读书讲座
甲
85
83
93
乙
92
86
86
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
(2)若“推荐语”“读书心得”“读书讲座”的成绩按2:3:5确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
【分析】(1)根据平均数的计算公式列出算式,求出平均数,进行比较,即可得出答案;
(2)根据加权平均数的计算公式列出算式,进行计算即可.
【解答】解:(1)乙最有可能获得大赛一等奖,
∵甲的平均成绩为=87(分)、乙的平均成绩为=88(分),
∴由87<88知乙最有可能获得大赛一等奖;
(2)甲最有可能获得大赛一等奖,
∵甲的加权平均成绩为=88.4(分)、乙的加权平均成绩为=87.2(分),
∴由88.4>87.2知甲最有可能获得大赛一等奖.
5.(2018春?永康市期末)为了响应“五水共治,建设美丽永康”的号召,某小区业委会随机调查了该小区20户家庭5月份的用水量,结果如下表:
5月份用水量(吨)
5
10
11
13
15
20
户数
3
5
6
3
2
1
(1)计算这20户家庭5月份的平均用水量;
(2)若该小区有800户家庭,估计该小区5月份用水量多少吨?
【分析】(1)根据加权平均数的定义求解;
(2)利用样本估计总体,利用20户的平均用水量乘以800可估计出该小区5月份的总用水量.
【解答】解:(1)这20户家庭5月份的平均用水量为=11(吨);
(2)估计该小区5月份用水量为800×11=8800吨.
6.(2018?镇江)某班50名学生的身高如下(单位:cm):
160 163 152 161 167 154 158 171 156 168
178 151 156 158 165 160 148 155 162 175
158 167 157 153 164 172 153 159 174 155
169 163 158 150 177 155 166 161 159 164
171 154 157 165 152 167 157 162 155 160
(1)小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本:161,155,174,163,152,请你计算小丽所抽取的这个样本的平均数;
(2)小丽将这50个数据按身高相差4cm分组,并制作了如下的表格:
身高
频数
频率
147.5~151.5
3
0.06
151.5~155.5
10
0.20
155.5~159.5
11
m
159.5~163.5
9
0.18
163.5~167.5
8
0.16
167.5~171.5
4
0.08
171.5~175.5
n
0.06
175.5~179.5
2
0.04
合计
50
1
①m= 0.22 ,n= 3 ;
②这50名学生身高的中位数落在哪个身高段内?身高在哪一段的学生数最多?
【分析】(1)利用平均数的计算公式计算即可;
(2)①完成表中信息,根据中位数的概念解答;
②根据众数的概念解答.
【解答】解:(1)=(161+155+174+163+152)=161;
(2)①如表可知,m=0,22,n=3,
故答案为:0.22;3;
②这50名学生身高的中位数落在159.5~163.5,
身高在151.5~155.5的学生数最多.
7.(2018?包头)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
【分析】(1)根据中位数的概念计算;
(2)根据题意列出方程,解方程即可;
(3)根据加权平均数的计算公式分别求出余三名候选人的综合成绩,比较即可.
【解答】解:(1)这四名候选人面试成绩的中位数为:=89(分);
(2)由题意得,x×60%+90×40%=87.6
解得,x=86,
答:表中x的值为86;
(3)甲候选人的综合成绩为:90×60%+88×40%=89.2(分),
乙候选人的综合成绩为:84×60%+92×40%=87.2(分),
丁候选人的综合成绩为:88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
8.(2018?贵阳)在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二:
69
97
96
89
98
100
99
100
95
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
92.8
97.5
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 135 人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
【分析】(1)根据中位数的定义求解可得;
(2)用初一、初二的总人数分别乘以其满分率,求和即可得;
(3)根据平均数和中位数的意义解答可得.
【解答】解:(1)由题意知初二年级的分数从小到大排列为69、69、79、79、89、94、95、96、97、97、98、98、99、99、99、99、100、100、100、100,
所以初二年级成绩的中位数为97.5分,
补全表格如下:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
92.8
97.5
20%
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共300×25%+300×20%=135人,
故答案为:135;
(3)初二年级掌握禁毒知识的总体水平较好,
∵初二年级的平均成绩比初一高,说明初二年级平均水平高,且初二年级成绩的中位数比初一大,说明初二年级的得高分人数多于初一,
∴初二年级掌握禁毒知识的总体水平较好.
9.(2018?陕西)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
各组总分/分
A
60<x≤70
38
2581
B
70<x≤80
72
5543
C
80<x≤90
60
5100
D
90<x≤100
m
2796
依据以上统计信息解答下列问题:
(1)求得m= 30 ,n= 19% ;
(2)这次测试成绩的中位数落在 B 组;
(3)求本次全部测试成绩的平均数.
【分析】(1)用B组人数除以其所占百分比求得总人数,再用总人数减去A、B、C组的人数可得m的值,用A组人数除以总人数可得n的值;
(2)根据中位数的定义求解可得;
(3)根据平均数的定义计算可得.
【解答】解:(1)∵被调查的学生总人数为72÷36%=200人,
∴m=200﹣(38+72+60)=30,n=×100%=19%,
故答案为:30、19%;
(2)∵共有200个数据,其中第100、101个数据均落在B组,
∴中位数落在B组,
故答案为:B;
(3)本次全部测试成绩的平均数为=80.1(分).
10.(2018?呼和浩特)下表是随机抽取的某公司部分员工的月收入资料.
月收入/元
45000
18000
10000
5500
5000
3400
3000
2000
人数
1
1
1
3
6
1
11
2
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论
;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
【分析】(1)要求平均数只要求出各个数据之和再除以数据个数即可;对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可;
(2)甲从员工平均工资水平的角度推断公司员工月收入,乙从员工中间工资水平的角度推断公司员工的收入;
(3)推断的合理性取决于数据的极差、某些数据的集中程度等因素.
【解答】解:(1)样本的平均数为:
=6150(元);
这组数据共有26个,第13、14个数据分别是3400、3000,
所以样本的中位数为:=3200(元).
(2)甲:由样本平均数6150元,估计公司全体员工月平均收入大约为6150元;
乙:由样本中位数为3200元,估计公司全体员工约有一半的月收入超过3200元,约有一半的月收入不足3200元.
(3)乙的推断比较科学合理.
由题意知样本中的26名员工,只有3名员工的收入在6150元以上,原因是该样本数据极差较大,
所以平均数不能真实的反映实际情况.
11.(2019?北碚区)某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整:
收集数据:从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
乙
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据:按如下分数段整理、描述这两组样本数据(请补全表格):
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
1
0
0
7
10
2
(说明:成绩80分及以上为生产技能优秀,70﹣79分为生产技能良好,60﹣69分为生产技能合格,60分以下为生产技能不合格)
分析数据:两组样本数据的平均数、中位数、众数如表所示(请补全表格):
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论:
(1)估计乙部门生产技能优秀的员工人数为 240人 ;
(2)你认为 甲或乙 部门员工的生产技能水平较高,说明理由(至少从两个不同的角度说明推断的合理性).
【分析】根据收集数据填写表格即可求解;用乙部门优秀员工人数除以20乘以400即可得出答案,根据情况进行讨论分析,理由合理即可.
【解答】解:乙在40≤x≤49有1人,在70≤x≤79有7人,在80≤x≤89有10人,在90≤x≤100有2人,
故答案为1,7,10,2.
甲的中位数为=77.5,乙的众数为81,
故答案为77.5,81.
(1)乙20人中优秀的员工有12人. ×400=240(人).
故估计乙部门生产技能优秀的员工人数为240人;
故答案为240人.
(2)答案不唯一,理由合理即可.
可以推断出甲部门员工的生产技能水平较高,理由为:
①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或可以推断出乙部门员工的生产技能水平较高,理由为:
①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
故答案为甲或乙.
12.(2019?九龙坡区)某市为提高环境质量对全市的环境污染进行综合治理,在治理的过程中环保部门随机选取了平安镇和富贵镇进行空气质量监测.
过程如下,请补充完整.
收集数据:
从2017年12月初开始连续一年对两镇的空气质量进行监测,将30天的空气污染指数(简称API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
平安镇:120 115 45 100 95 50 80 70 85 50 50 100
富贵镇:110 90 105 80 90 85 90 50 90 45 70 60
(1)整理、描述数据:
按下表整理、描述这两镇空气污染指数的数据:
空气质量为优
空气质量为良
空气质量为轻微污染
平安镇
4
6
2
富贵镇
1
9
2
(说明空气污染指数<50时,空气质量为优;50≤空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻度污染)
(2)分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇
平均数
中位数
众数
平安镇
80
82.5
50
富贵镇
81.3
87.5
90
请将以上两个表格补充完整;
(3)得出结论:可以推断出 平安镇 镇这一年中环境状况比较好,理由: 平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等 .(至少从两个不同的角度说明推断的合理性)
【分析】(1)首先根据空气污染指数的数据及空气优、良和轻度污染的标准,对富贵镇进行分类并填空;
(2)根据众数和平均数的定义,计算出平安镇的中位数和富贵镇的众数;
(3)根据表格的平均数、中位数、众数对两个镇的情况作出一个简单的判断即可.
【解答】解:(1)富贵镇空气质量为优的天数是1天;空气质量为良的天数为9天;空气质量为轻微污染的天数为2天;
故答案为:1,9,2
(2)平安镇:120 115 100 100 95 85 80 70 50 50 50 45,
其中位于中间的两个数是85和80,所以其中位数为=82.5;
富贵镇的数据中,90出现了四次,出现的次数最多,故其众数为90.
故答案为82.5,90.
(3)平安镇的环境状况较好.
例如:平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等;
故答案为:平安镇;平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等.
13.(2018?南通)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17
18
16
13
24
15
28
26
18
19
22
17
16
19
32
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别
一
二
三
四
五
六
七
销售额
13≤x<16
16≤x<19
19≤x<22
22≤x<25
25≤x<28
28≤x<31
31≤x<34
频数
7
9
3
a
2
b
2
数据分析表
平均数
众数
中位数
20.3
c
18
请根据以上信息解答下列问题:
(1)填空:a= 3 ,b= 4 ,c= 15 ;
(2)若将月销售额不低于25万元确定为销售目标,则有 8 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
【分析】(1)从表中数出落在22≤x<25和28≤x<31范围内的数据个数得到a、b的值,利用众数定义确定c的值;
(2)利用频数分布表,后面三组的频数和为获得奖励的营业员的数量;
(3)利用中位数的意义进行回答.
【解答】解:(1)在22≤x<25范围内的数据有3个,在28≤x<31范围内的数据有4个,
15出现的次数最大,则众数为15;
(2)月销售额不低于25万元为后面三组数据,即有8位营业员获得奖励;
故答案为3,4,15;8;
(3)想让一半左右的营业员都能达到销售目标,我认为月销售额定为18万合适.
因为中位数为18,即大于18与小于18的人数一样多,
所以月销售额定为18万,有一半左右的营业员能达到销售目标.
14.(2018?渝中区)某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
【分析】(1)由12岁的人数及其所占百分比可得样本容量;
(2)先求出14、16岁的人数,再根据平均数、众数和中位数的定义求解可得;
(3)用总人数乘以样本中15、16岁的人数所占比例可得.
【解答】解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
15.(2018?云南)某同学参加了学校举行的“五好小公民?红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
【分析】(1)根据众数与中位数的定义求解即可;
(2)根据平均数的定义求解即可.
【解答】解:(1)从小到大排列此数据为:5,6,7,7,8,8,8,
数据8出现了三次最多为众数,
7处在第4位为中位数;
(2)该同学所得分数的平均数为(5+6+7×2+8×3)÷7=7.
16.(2018?咸宁)近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是 3 ,众数是 3 ,该中位数的意义是 表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次) ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【分析】(1)根据中位数和众数的定义求解可得;
(2)根据加权平均数的公式列式计算即可;
(3)用总人数乘以样本中使用共享单车次数在3次以上(含3次)的学生所占比例即可得.
【解答】解:(1)∵总人数为11+15+23+28+18+5=100,
∴中位数为第50、51个数据的平均数,即中位数为=3次,众数为3次,
其中中位数表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次),
故答案为:3、3、表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次);
(2)=≈2(次),
答:这天部分出行学生平均每人使用共享单车约2次;
(3)1500×=765(人),
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
17.(2018?广州)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 16 ,众数是 17 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
【分析】(1)将数据按照大小顺序重新排列,计算出中间两个数的平均数即是中位数,出现次数最多的即为众数;
(2)根据平均数的概念,将所有数的和除以10即可;
(3)用样本平均数估算总体的平均数.
【解答】解:(1)按照大小顺序重新排列后,第5、第6个数分别是15和17,所以中位数是(15+17)÷2=16,17出现3次最多,所以众数是17,
故答案是16,17;
(2)=14,
答:这10位居民一周内使用共享单车的平均次数是14次;
(3)200×14=2800
答:该小区居民一周内使用共享单车的总次数为2800次.
18.(2019?沙坪坝区)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
组别
频数
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
6
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
b
43.1
乙车间
180
180
180
22.6
应用数据:
(1)请写出表中a= 9 ,b= 180 mm;
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
【分析】(1)根据个体与总体的关系求出a即可,根据中位数的定义判断即可.
(2)利用样本估计总体的思想解决问题即可.
(3)从合格率,方差判断即可.
【解答】解:(1)a=20﹣1﹣2﹣6﹣2=9,
根据中位数的定义可知甲的中位数为180mm,
故答案为9,180.
(2)估计乙车间生产的1000个该款新产品中合格产品有:1000×=750(个).
(3)从合格率看:甲的合格率:×100%=55%,
乙的合格率:×100%=75%,
∴乙车间生产的新产品好.
从方差看,乙的方差小,乙车间生产的新产品好.
综上所述,乙车间生产的新产品好.
19.(2019?渝中区)某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分)
整理,分析过程如下:
成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
0
1
4
5
0
0
乙
1
1
4
2
1
1
(1)两组数据的极差、平均数、中位数、众数、方差如下表所示,请补充完整:
学生
极差
平均数
中位数
众数
方差
甲
14
83.7
86
86
13.21
乙
24
83.7
82
81
46.21
(2)若从甲、乙两人中选择一人参加知识竞赛,你会选 甲或乙 (填“甲“或“乙“),理由为 从极差、中位数、众数、方差来看,甲的成绩比较好或从发展趋势看,乙的成绩越来越好 .
【分析】(1)根据极差,中位数,众数的定义判断即可;
(2)从极差、中位数、众数、方差来看,甲的成绩比较好,选甲.从发展趋势看,乙的成绩越来越好,选乙.
【解答】解:(1)甲的极差为14,中位数为86,
乙的众数为81.
故答案为14,86,81.
(2)从极差、中位数、众数、方差来看,甲的成绩比较好,选甲.
从发展趋势看,乙的成绩越来越好,选乙.
20.(2018?荆州)为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
19.2
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
【分析】(1)根据平均数、中位数、众数的概念解答即可;
(2)根据它们的方差,从而可以解答本题.
【解答】解:(1)a=,b=85,c=85,
(2)∵22.8>19.2,
∴八(2)班前5名同学的成绩较好,
21.(2018?吉林)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况,质检员进行了抽样调查,过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:g)如下:
甲:400,400,408,406,410,409,400,393,394,395
乙:403,404,396,399,402,402,405,397,402,398
整理数据:
表一
质量(g)
频数
种类
393≤x<396
396≤x<399
399≤x<402
402≤x<405
405≤x<408
408≤x<411
甲
3
0
3
0
1
3
乙
0
3
1
5
1
0
分析数据:
表二
种类
平均数
中位数
众数
方差
甲
401.5
400
400
36.85
乙
400.8
402
402
8.56
得出结论:
包装机分装情况比较好的是 乙 (填甲或乙),说明你的理由.
【分析】整理数据:由题干中的数据结合表中范围确定个数即可得;
分析数据:根据众数和中位数的定义求解可得;
得出结论:根据方差的意义,方差小分装质量较为稳定即可得.
【解答】解:整理数据:
表一
质量(g)
频数
种类
393≤x<396
396≤x<399
399≤x<402
402≤x<405
405≤x<408
408≤x<411
甲
3
0
3
0
1
3
乙
0
3
1
5
1
0
分析数据:
将甲组数据重新排列为:393、394、395、400、400、400、406、408、409、410,
∴甲组数据的中位数为400;
乙组数据中402出现次数最多,有3次,
∴乙组数据的众数为402;
表二
种类
平均数
中位数
众数
方差
甲
401.5
400
400
36.85
乙
400.8
402
402
8.56
得出结论:
表二知,乙包装机分装的奶粉质量的方差小,分装质量比较稳定,
所以包装机分装情况比较好的是乙.
故答案为:乙.
22.(2018?舟山)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
b
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
180
22.6
应用数据:
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
【分析】(1)利用所列举的数据得出甲车间样品的合格率;
(2)得出乙车间样品的合格产品数进而得出乙车间样品的合格率进而得出答案;
(3)利用平均数、方差的意义分别分析得出答案.
【解答】解:(1)甲车间样品的合格率为:×100%=55%;
(2)∵乙车间样品的合格产品数为:20﹣(1+2+2)=15(个),
∴乙车间样品的合格率为:×100%=75%,
∴乙车间的合格产品数为:1000×75%=750(个);
(3)①乙车间合格率比甲车间高,所以乙车间生产的新产品更好;
②甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比较稳定,所以乙车间生产的新产品更好.
23.(2018?江西)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min)
0≤x<40
40≤x<80
80≤x<120
120≤x<160
等级
D
C
B
A
人数
3
5
8
4
分析数据:补全下列表格中的统计量:
平均数
中位数
众数
80
81
81
得出结论:
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 B ;
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
【分析】根据中位数、众数的定义可以填表格,利用样本和总体之间的比例关系可以估计或计算得到(1)(2)(3)结果.
【解答】解:(1)根据上表统计显示:样本中位数和众数都是81,平均数是80,都是B等级,
故估计该校学生每周的用于课外阅读时间的情况等级为B.
(2)∵=160
∴该校现有学生400人,估计等级为“B”的学生有160名.
(3)以平均数来估计:
×52=26
∴假设平均阅读一本课外书的时间为160分钟,以样本的平均数来估计该校学生每人一年(按52周计算)平均阅读26本课外书.
故答案为:5,4,81,81,B;
24.(2018?威海)为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 4.5首 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【分析】(1)根据统计图中的数据可以求得这组数据的中位数;
(2)根据表格中的数据可以解答本题;
(3)根据统计图和表格中的数据可以分别计算出比赛前后的众数和中位数,从而可以解答本题.
【解答】解:(1)本次调查的学生有:20÷=120(名),
背诵4首的有:120﹣15﹣20﹣16﹣13﹣11=45(人),
∵15+45=60,
∴这组数据的中位数是:(4+5)÷2=4.5(首),
故答案为:4.5首;
(2)大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有:1200×=850(人),
答:大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有850人;
(3)活动启动之初的中位数是4.5首,众数是4首,
大赛比赛后一个月时的中位数是6首,众数是6首,
由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想.
一.解答题(共24小题)
1.(2018?柳州)一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
2.(2018?南京)随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2200
1780
7560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
3.(2018春?凉州区期末)某次歌咏比赛,前三名选手的成绩统计如下:(单位:分)
测试项目
测试成绩
王晓丽
李真
林飞扬
唱功
98
95
80
音乐常识
80
90
100
综合知识
80
90
100
将唱功、音乐常识综合知识三项测试成绩按6:3:1的加权平均分排出冠军、亚军季军,则冠军、亚军、季军各是谁?
4.(2018春?孝义市期末)2018年4月23日是第23个世界读书日.为迎接第23个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者
推荐语
读书心得
读书讲座
甲
85
83
93
乙
92
86
86
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
(2)若“推荐语”“读书心得”“读书讲座”的成绩按2:3:5确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
5.(2018春?永康市期末)为了响应“五水共治,建设美丽永康”的号召,某小区业委会随机调查了该小区20户家庭5月份的用水量,结果如下表:
5月份用水量(吨)
5
10
11
13
15
20
户数
3
5
6
3
2
1
(1)计算这20户家庭5月份的平均用水量;
(2)若该小区有800户家庭,估计该小区5月份用水量多少吨?
6.(2018?镇江)某班50名学生的身高如下(单位:cm):
160 163 152 161 167 154 158 171 156 168
178 151 156 158 165 160 148 155 162 175
158 167 157 153 164 172 153 159 174 155
169 163 158 150 177 155 166 161 159 164
171 154 157 165 152 167 157 162 155 160
(1)小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本:161,155,174,163,152,请你计算小丽所抽取的这个样本的平均数;
(2)小丽将这50个数据按身高相差4cm分组,并制作了如下的表格:
身高
频数
频率
147.5~151.5
0.06
151.5~155.5
155.5~159.5
11
m
159.5~163.5
0.18
163.5~167.5
8
0.16
167.5~171.5
4
171.5~175.5
n
0.06
175.5~179.5
2
合计
50
1
①m= ,n= ;
②这50名学生身高的中位数落在哪个身高段内?身高在哪一段的学生数最多?
7.(2018?包头)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
8.(2018?贵阳)在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二:
69
97
96
89
98
100
99
100
95
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
92.8
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
9.(2018?陕西)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
各组总分/分
A
60<x≤70
38
2581
B
70<x≤80
72
5543
C
80<x≤90
60
5100
D
90<x≤100
m
2796
依据以上统计信息解答下列问题:
(1)求得m= ,n= ;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
10.(2018?呼和浩特)下表是随机抽取的某公司部分员工的月收入资料.
月收入/元
45000
18000
10000
5500
5000
3400
3000
2000
人数
1
1
1
3
6
1
11
2
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论
;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
11.(2019?北碚区)某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整:
收集数据:从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
乙
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据:按如下分数段整理、描述这两组样本数据(请补全表格):
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
0
0
(说明:成绩80分及以上为生产技能优秀,70﹣79分为生产技能良好,60﹣69分为生产技能合格,60分以下为生产技能不合格)
分析数据:两组样本数据的平均数、中位数、众数如表所示(请补全表格):
部门
平均数
中位数
众数
甲
78.3
75
乙
78
80.5
得出结论:
(1)估计乙部门生产技能优秀的员工人数为 ;
(2)你认为 部门员工的生产技能水平较高,说明理由(至少从两个不同的角度说明推断的合理性).
12.(2019?九龙坡区)某市为提高环境质量对全市的环境污染进行综合治理,在治理的过程中环保部门随机选取了平安镇和富贵镇进行空气质量监测.
过程如下,请补充完整.
收集数据:
从2017年12月初开始连续一年对两镇的空气质量进行监测,将30天的空气污染指数(简称API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
平安镇:120 115 45 100 95 50 80 70 85 50 50 100
富贵镇:110 90 105 80 90 85 90 50 90 45 70 60
(1)整理、描述数据:
按下表整理、描述这两镇空气污染指数的数据:
空气质量为优
空气质量为良
空气质量为轻微污染
平安镇
4
6
2
富贵镇
(说明空气污染指数<50时,空气质量为优;50≤空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻度污染)
(2)分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇
平均数
中位数
众数
平安镇
80
50
富贵镇
81.3
87.5
请将以上两个表格补充完整;
(3)得出结论:可以推断出 镇这一年中环境状况比较好,理由: .(至少从两个不同的角度说明推断的合理性)
13.(2018?南通)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17
18
16
13
24
15
28
26
18
19
22
17
16
19
32
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别
一
二
三
四
五
六
七
销售额
13≤x<16
16≤x<19
19≤x<22
22≤x<25
25≤x<28
28≤x<31
31≤x<34
频数
7
9
3
a
2
b
2
数据分析表
平均数
众数
中位数
20.3
c
18
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
14.(2018?渝中区)某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
15.(2018?云南)某同学参加了学校举行的“五好小公民?红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
16.(2018?咸宁)近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
17.(2018?广州)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
18.(2019?沙坪坝区)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
组别
频数
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
6
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
b
43.1
乙车间
180
180
180
22.6
应用数据:
(1)请写出表中a= ,b= mm;
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
19.(2019?渝中区)某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分)
整理,分析过程如下:
成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
0
1
4
5
0
0
乙
1
1
4
2
1
1
(1)两组数据的极差、平均数、中位数、众数、方差如下表所示,请补充完整:
学生
极差
平均数
中位数
众数
方差
甲
83.7
86
13.21
乙
24
83.7
82
46.21
(2)若从甲、乙两人中选择一人参加知识竞赛,你会选 (填“甲“或“乙“),理由为 .
20.(2018?荆州)为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
19.2
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
21.(2018?吉林)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况,质检员进行了抽样调查,过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:g)如下:
甲:400,400,408,406,410,409,400,393,394,395
乙:403,404,396,399,402,402,405,397,402,398
整理数据:
表一
质量(g)
频数
种类
393≤x<396
396≤x<399
399≤x<402
402≤x<405
405≤x<408
408≤x<411
甲
3
0
0
1
3
乙
0
1
5
0
分析数据:
表二
种类
平均数
中位数
众数
方差
甲
401.5
400
36.85
乙
400.8
402
8.56
得出结论:
包装机分装情况比较好的是 (填甲或乙),说明你的理由.
22.(2018?舟山)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
b
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
180
22.6
应用数据:
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
23.(2018?江西)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min)
0≤x<40
40≤x<80
80≤x<120
120≤x<160
等级
D
C
B
A
人数
3
8
分析数据:补全下列表格中的统计量:
平均数
中位数
众数
80
得出结论:
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
24.(2018?威海)为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
人教版八下第20章数据的分析复习题---解答题
参考答案与试题解析
一.解答题(共24小题)
1.(2018?柳州)一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
【分析】平均数是指在一组数据中所有数据之和再除以数据的个数.
【解答】解:该同学这五次投实心球的平均成绩为:
=10.4.
故该同学这五次投实心球的平均成绩为10.4m.
2.(2018?南京)随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2200
1780
7560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
【分析】(1)根据平均数的定义计算可得;
(2)从极端值对平均数的影响作出判断,可用该店本周一到周日的日均营业额估计当月营业额.
【解答】解:(1)该店本周的日平均营业额为7560÷7=1080元;
(2)因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额,
所以去掉周六、日的营业额对平均数的影响较大,
故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合理,
方案:用该店本周一到周日的日均营业额估计当月营业额,
当月的营业额为30×1080=32400元.
3.(2018春?凉州区期末)某次歌咏比赛,前三名选手的成绩统计如下:(单位:分)
测试项目
测试成绩
王晓丽
李真
林飞扬
唱功
98
95
80
音乐常识
80
90
100
综合知识
80
90
100
将唱功、音乐常识综合知识三项测试成绩按6:3:1的加权平均分排出冠军、亚军季军,则冠军、亚军、季军各是谁?
【分析】根据加权平均数的计算公式先分别求出三个人的最后得分,再进行比较即可.
【解答】解:王晓丽的成绩是:(98×6+80×3+80)÷10=90.8(分);
李真:(95×6+90×3+90)÷10=93(分);
林飞杨:(80×6+100×3+100)÷10=88(分).
∵93>90.8>88,
∴冠军是李真、亚军是王晓丽、季军是林飞杨.
4.(2018春?孝义市期末)2018年4月23日是第23个世界读书日.为迎接第23个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者
推荐语
读书心得
读书讲座
甲
85
83
93
乙
92
86
86
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
(2)若“推荐语”“读书心得”“读书讲座”的成绩按2:3:5确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由
【分析】(1)根据平均数的计算公式列出算式,求出平均数,进行比较,即可得出答案;
(2)根据加权平均数的计算公式列出算式,进行计算即可.
【解答】解:(1)乙最有可能获得大赛一等奖,
∵甲的平均成绩为=87(分)、乙的平均成绩为=88(分),
∴由87<88知乙最有可能获得大赛一等奖;
(2)甲最有可能获得大赛一等奖,
∵甲的加权平均成绩为=88.4(分)、乙的加权平均成绩为=87.2(分),
∴由88.4>87.2知甲最有可能获得大赛一等奖.
5.(2018春?永康市期末)为了响应“五水共治,建设美丽永康”的号召,某小区业委会随机调查了该小区20户家庭5月份的用水量,结果如下表:
5月份用水量(吨)
5
10
11
13
15
20
户数
3
5
6
3
2
1
(1)计算这20户家庭5月份的平均用水量;
(2)若该小区有800户家庭,估计该小区5月份用水量多少吨?
【分析】(1)根据加权平均数的定义求解;
(2)利用样本估计总体,利用20户的平均用水量乘以800可估计出该小区5月份的总用水量.
【解答】解:(1)这20户家庭5月份的平均用水量为=11(吨);
(2)估计该小区5月份用水量为800×11=8800吨.
6.(2018?镇江)某班50名学生的身高如下(单位:cm):
160 163 152 161 167 154 158 171 156 168
178 151 156 158 165 160 148 155 162 175
158 167 157 153 164 172 153 159 174 155
169 163 158 150 177 155 166 161 159 164
171 154 157 165 152 167 157 162 155 160
(1)小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本:161,155,174,163,152,请你计算小丽所抽取的这个样本的平均数;
(2)小丽将这50个数据按身高相差4cm分组,并制作了如下的表格:
身高
频数
频率
147.5~151.5
3
0.06
151.5~155.5
10
0.20
155.5~159.5
11
m
159.5~163.5
9
0.18
163.5~167.5
8
0.16
167.5~171.5
4
0.08
171.5~175.5
n
0.06
175.5~179.5
2
0.04
合计
50
1
①m= 0.22 ,n= 3 ;
②这50名学生身高的中位数落在哪个身高段内?身高在哪一段的学生数最多?
【分析】(1)利用平均数的计算公式计算即可;
(2)①完成表中信息,根据中位数的概念解答;
②根据众数的概念解答.
【解答】解:(1)=(161+155+174+163+152)=161;
(2)①如表可知,m=0,22,n=3,
故答案为:0.22;3;
②这50名学生身高的中位数落在159.5~163.5,
身高在151.5~155.5的学生数最多.
7.(2018?包头)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
【分析】(1)根据中位数的概念计算;
(2)根据题意列出方程,解方程即可;
(3)根据加权平均数的计算公式分别求出余三名候选人的综合成绩,比较即可.
【解答】解:(1)这四名候选人面试成绩的中位数为:=89(分);
(2)由题意得,x×60%+90×40%=87.6
解得,x=86,
答:表中x的值为86;
(3)甲候选人的综合成绩为:90×60%+88×40%=89.2(分),
乙候选人的综合成绩为:84×60%+92×40%=87.2(分),
丁候选人的综合成绩为:88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
8.(2018?贵阳)在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二:
69
97
96
89
98
100
99
100
95
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
92.8
97.5
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 135 人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
【分析】(1)根据中位数的定义求解可得;
(2)用初一、初二的总人数分别乘以其满分率,求和即可得;
(3)根据平均数和中位数的意义解答可得.
【解答】解:(1)由题意知初二年级的分数从小到大排列为69、69、79、79、89、94、95、96、97、97、98、98、99、99、99、99、100、100、100、100,
所以初二年级成绩的中位数为97.5分,
补全表格如下:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
92.8
97.5
20%
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共300×25%+300×20%=135人,
故答案为:135;
(3)初二年级掌握禁毒知识的总体水平较好,
∵初二年级的平均成绩比初一高,说明初二年级平均水平高,且初二年级成绩的中位数比初一大,说明初二年级的得高分人数多于初一,
∴初二年级掌握禁毒知识的总体水平较好.
9.(2018?陕西)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
各组总分/分
A
60<x≤70
38
2581
B
70<x≤80
72
5543
C
80<x≤90
60
5100
D
90<x≤100
m
2796
依据以上统计信息解答下列问题:
(1)求得m= 30 ,n= 19% ;
(2)这次测试成绩的中位数落在 B 组;
(3)求本次全部测试成绩的平均数.
【分析】(1)用B组人数除以其所占百分比求得总人数,再用总人数减去A、B、C组的人数可得m的值,用A组人数除以总人数可得n的值;
(2)根据中位数的定义求解可得;
(3)根据平均数的定义计算可得.
【解答】解:(1)∵被调查的学生总人数为72÷36%=200人,
∴m=200﹣(38+72+60)=30,n=×100%=19%,
故答案为:30、19%;
(2)∵共有200个数据,其中第100、101个数据均落在B组,
∴中位数落在B组,
故答案为:B;
(3)本次全部测试成绩的平均数为=80.1(分).
10.(2018?呼和浩特)下表是随机抽取的某公司部分员工的月收入资料.
月收入/元
45000
18000
10000
5500
5000
3400
3000
2000
人数
1
1
1
3
6
1
11
2
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论
;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
【分析】(1)要求平均数只要求出各个数据之和再除以数据个数即可;对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可;
(2)甲从员工平均工资水平的角度推断公司员工月收入,乙从员工中间工资水平的角度推断公司员工的收入;
(3)推断的合理性取决于数据的极差、某些数据的集中程度等因素.
【解答】解:(1)样本的平均数为:
=6150(元);
这组数据共有26个,第13、14个数据分别是3400、3000,
所以样本的中位数为:=3200(元).
(2)甲:由样本平均数6150元,估计公司全体员工月平均收入大约为6150元;
乙:由样本中位数为3200元,估计公司全体员工约有一半的月收入超过3200元,约有一半的月收入不足3200元.
(3)乙的推断比较科学合理.
由题意知样本中的26名员工,只有3名员工的收入在6150元以上,原因是该样本数据极差较大,
所以平均数不能真实的反映实际情况.
11.(2019?北碚区)某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整:
收集数据:从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
乙
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据:按如下分数段整理、描述这两组样本数据(请补全表格):
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
1
0
0
7
10
2
(说明:成绩80分及以上为生产技能优秀,70﹣79分为生产技能良好,60﹣69分为生产技能合格,60分以下为生产技能不合格)
分析数据:两组样本数据的平均数、中位数、众数如表所示(请补全表格):
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论:
(1)估计乙部门生产技能优秀的员工人数为 240人 ;
(2)你认为 甲或乙 部门员工的生产技能水平较高,说明理由(至少从两个不同的角度说明推断的合理性).
【分析】根据收集数据填写表格即可求解;用乙部门优秀员工人数除以20乘以400即可得出答案,根据情况进行讨论分析,理由合理即可.
【解答】解:乙在40≤x≤49有1人,在70≤x≤79有7人,在80≤x≤89有10人,在90≤x≤100有2人,
故答案为1,7,10,2.
甲的中位数为=77.5,乙的众数为81,
故答案为77.5,81.
(1)乙20人中优秀的员工有12人. ×400=240(人).
故估计乙部门生产技能优秀的员工人数为240人;
故答案为240人.
(2)答案不唯一,理由合理即可.
可以推断出甲部门员工的生产技能水平较高,理由为:
①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或可以推断出乙部门员工的生产技能水平较高,理由为:
①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
故答案为甲或乙.
12.(2019?九龙坡区)某市为提高环境质量对全市的环境污染进行综合治理,在治理的过程中环保部门随机选取了平安镇和富贵镇进行空气质量监测.
过程如下,请补充完整.
收集数据:
从2017年12月初开始连续一年对两镇的空气质量进行监测,将30天的空气污染指数(简称API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
平安镇:120 115 45 100 95 50 80 70 85 50 50 100
富贵镇:110 90 105 80 90 85 90 50 90 45 70 60
(1)整理、描述数据:
按下表整理、描述这两镇空气污染指数的数据:
空气质量为优
空气质量为良
空气质量为轻微污染
平安镇
4
6
2
富贵镇
1
9
2
(说明空气污染指数<50时,空气质量为优;50≤空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻度污染)
(2)分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇
平均数
中位数
众数
平安镇
80
82.5
50
富贵镇
81.3
87.5
90
请将以上两个表格补充完整;
(3)得出结论:可以推断出 平安镇 镇这一年中环境状况比较好,理由: 平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等 .(至少从两个不同的角度说明推断的合理性)
【分析】(1)首先根据空气污染指数的数据及空气优、良和轻度污染的标准,对富贵镇进行分类并填空;
(2)根据众数和平均数的定义,计算出平安镇的中位数和富贵镇的众数;
(3)根据表格的平均数、中位数、众数对两个镇的情况作出一个简单的判断即可.
【解答】解:(1)富贵镇空气质量为优的天数是1天;空气质量为良的天数为9天;空气质量为轻微污染的天数为2天;
故答案为:1,9,2
(2)平安镇:120 115 100 100 95 85 80 70 50 50 50 45,
其中位于中间的两个数是85和80,所以其中位数为=82.5;
富贵镇的数据中,90出现了四次,出现的次数最多,故其众数为90.
故答案为82.5,90.
(3)平安镇的环境状况较好.
例如:平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等;
故答案为:平安镇;平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等.
13.(2018?南通)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17
18
16
13
24
15
28
26
18
19
22
17
16
19
32
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别
一
二
三
四
五
六
七
销售额
13≤x<16
16≤x<19
19≤x<22
22≤x<25
25≤x<28
28≤x<31
31≤x<34
频数
7
9
3
a
2
b
2
数据分析表
平均数
众数
中位数
20.3
c
18
请根据以上信息解答下列问题:
(1)填空:a= 3 ,b= 4 ,c= 15 ;
(2)若将月销售额不低于25万元确定为销售目标,则有 8 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
【分析】(1)从表中数出落在22≤x<25和28≤x<31范围内的数据个数得到a、b的值,利用众数定义确定c的值;
(2)利用频数分布表,后面三组的频数和为获得奖励的营业员的数量;
(3)利用中位数的意义进行回答.
【解答】解:(1)在22≤x<25范围内的数据有3个,在28≤x<31范围内的数据有4个,
15出现的次数最大,则众数为15;
(2)月销售额不低于25万元为后面三组数据,即有8位营业员获得奖励;
故答案为3,4,15;8;
(3)想让一半左右的营业员都能达到销售目标,我认为月销售额定为18万合适.
因为中位数为18,即大于18与小于18的人数一样多,
所以月销售额定为18万,有一半左右的营业员能达到销售目标.
14.(2018?渝中区)某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
【分析】(1)由12岁的人数及其所占百分比可得样本容量;
(2)先求出14、16岁的人数,再根据平均数、众数和中位数的定义求解可得;
(3)用总人数乘以样本中15、16岁的人数所占比例可得.
【解答】解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
15.(2018?云南)某同学参加了学校举行的“五好小公民?红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
【分析】(1)根据众数与中位数的定义求解即可;
(2)根据平均数的定义求解即可.
【解答】解:(1)从小到大排列此数据为:5,6,7,7,8,8,8,
数据8出现了三次最多为众数,
7处在第4位为中位数;
(2)该同学所得分数的平均数为(5+6+7×2+8×3)÷7=7.
16.(2018?咸宁)近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是 3 ,众数是 3 ,该中位数的意义是 表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次) ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【分析】(1)根据中位数和众数的定义求解可得;
(2)根据加权平均数的公式列式计算即可;
(3)用总人数乘以样本中使用共享单车次数在3次以上(含3次)的学生所占比例即可得.
【解答】解:(1)∵总人数为11+15+23+28+18+5=100,
∴中位数为第50、51个数据的平均数,即中位数为=3次,众数为3次,
其中中位数表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次),
故答案为:3、3、表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次);
(2)=≈2(次),
答:这天部分出行学生平均每人使用共享单车约2次;
(3)1500×=765(人),
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
17.(2018?广州)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 16 ,众数是 17 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
【分析】(1)将数据按照大小顺序重新排列,计算出中间两个数的平均数即是中位数,出现次数最多的即为众数;
(2)根据平均数的概念,将所有数的和除以10即可;
(3)用样本平均数估算总体的平均数.
【解答】解:(1)按照大小顺序重新排列后,第5、第6个数分别是15和17,所以中位数是(15+17)÷2=16,17出现3次最多,所以众数是17,
故答案是16,17;
(2)=14,
答:这10位居民一周内使用共享单车的平均次数是14次;
(3)200×14=2800
答:该小区居民一周内使用共享单车的总次数为2800次.
18.(2019?沙坪坝区)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
组别
频数
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
6
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
b
43.1
乙车间
180
180
180
22.6
应用数据:
(1)请写出表中a= 9 ,b= 180 mm;
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
【分析】(1)根据个体与总体的关系求出a即可,根据中位数的定义判断即可.
(2)利用样本估计总体的思想解决问题即可.
(3)从合格率,方差判断即可.
【解答】解:(1)a=20﹣1﹣2﹣6﹣2=9,
根据中位数的定义可知甲的中位数为180mm,
故答案为9,180.
(2)估计乙车间生产的1000个该款新产品中合格产品有:1000×=750(个).
(3)从合格率看:甲的合格率:×100%=55%,
乙的合格率:×100%=75%,
∴乙车间生产的新产品好.
从方差看,乙的方差小,乙车间生产的新产品好.
综上所述,乙车间生产的新产品好.
19.(2019?渝中区)某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分)
整理,分析过程如下:
成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
0
1
4
5
0
0
乙
1
1
4
2
1
1
(1)两组数据的极差、平均数、中位数、众数、方差如下表所示,请补充完整:
学生
极差
平均数
中位数
众数
方差
甲
14
83.7
86
86
13.21
乙
24
83.7
82
81
46.21
(2)若从甲、乙两人中选择一人参加知识竞赛,你会选 甲或乙 (填“甲“或“乙“),理由为 从极差、中位数、众数、方差来看,甲的成绩比较好或从发展趋势看,乙的成绩越来越好 .
【分析】(1)根据极差,中位数,众数的定义判断即可;
(2)从极差、中位数、众数、方差来看,甲的成绩比较好,选甲.从发展趋势看,乙的成绩越来越好,选乙.
【解答】解:(1)甲的极差为14,中位数为86,
乙的众数为81.
故答案为14,86,81.
(2)从极差、中位数、众数、方差来看,甲的成绩比较好,选甲.
从发展趋势看,乙的成绩越来越好,选乙.
20.(2018?荆州)为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
19.2
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
【分析】(1)根据平均数、中位数、众数的概念解答即可;
(2)根据它们的方差,从而可以解答本题.
【解答】解:(1)a=,b=85,c=85,
(2)∵22.8>19.2,
∴八(2)班前5名同学的成绩较好,
21.(2018?吉林)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况,质检员进行了抽样调查,过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:g)如下:
甲:400,400,408,406,410,409,400,393,394,395
乙:403,404,396,399,402,402,405,397,402,398
整理数据:
表一
质量(g)
频数
种类
393≤x<396
396≤x<399
399≤x<402
402≤x<405
405≤x<408
408≤x<411
甲
3
0
3
0
1
3
乙
0
3
1
5
1
0
分析数据:
表二
种类
平均数
中位数
众数
方差
甲
401.5
400
400
36.85
乙
400.8
402
402
8.56
得出结论:
包装机分装情况比较好的是 乙 (填甲或乙),说明你的理由.
【分析】整理数据:由题干中的数据结合表中范围确定个数即可得;
分析数据:根据众数和中位数的定义求解可得;
得出结论:根据方差的意义,方差小分装质量较为稳定即可得.
【解答】解:整理数据:
表一
质量(g)
频数
种类
393≤x<396
396≤x<399
399≤x<402
402≤x<405
405≤x<408
408≤x<411
甲
3
0
3
0
1
3
乙
0
3
1
5
1
0
分析数据:
将甲组数据重新排列为:393、394、395、400、400、400、406、408、409、410,
∴甲组数据的中位数为400;
乙组数据中402出现次数最多,有3次,
∴乙组数据的众数为402;
表二
种类
平均数
中位数
众数
方差
甲
401.5
400
400
36.85
乙
400.8
402
402
8.56
得出结论:
表二知,乙包装机分装的奶粉质量的方差小,分装质量比较稳定,
所以包装机分装情况比较好的是乙.
故答案为:乙.
22.(2018?舟山)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
a
b
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
180
22.6
应用数据:
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
【分析】(1)利用所列举的数据得出甲车间样品的合格率;
(2)得出乙车间样品的合格产品数进而得出乙车间样品的合格率进而得出答案;
(3)利用平均数、方差的意义分别分析得出答案.
【解答】解:(1)甲车间样品的合格率为:×100%=55%;
(2)∵乙车间样品的合格产品数为:20﹣(1+2+2)=15(个),
∴乙车间样品的合格率为:×100%=75%,
∴乙车间的合格产品数为:1000×75%=750(个);
(3)①乙车间合格率比甲车间高,所以乙车间生产的新产品更好;
②甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比较稳定,所以乙车间生产的新产品更好.
23.(2018?江西)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min)
0≤x<40
40≤x<80
80≤x<120
120≤x<160
等级
D
C
B
A
人数
3
5
8
4
分析数据:补全下列表格中的统计量:
平均数
中位数
众数
80
81
81
得出结论:
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 B ;
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
【分析】根据中位数、众数的定义可以填表格,利用样本和总体之间的比例关系可以估计或计算得到(1)(2)(3)结果.
【解答】解:(1)根据上表统计显示:样本中位数和众数都是81,平均数是80,都是B等级,
故估计该校学生每周的用于课外阅读时间的情况等级为B.
(2)∵=160
∴该校现有学生400人,估计等级为“B”的学生有160名.
(3)以平均数来估计:
×52=26
∴假设平均阅读一本课外书的时间为160分钟,以样本的平均数来估计该校学生每人一年(按52周计算)平均阅读26本课外书.
故答案为:5,4,81,81,B;
24.(2018?威海)为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 4.5首 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【分析】(1)根据统计图中的数据可以求得这组数据的中位数;
(2)根据表格中的数据可以解答本题;
(3)根据统计图和表格中的数据可以分别计算出比赛前后的众数和中位数,从而可以解答本题.
【解答】解:(1)本次调查的学生有:20÷=120(名),
背诵4首的有:120﹣15﹣20﹣16﹣13﹣11=45(人),
∵15+45=60,
∴这组数据的中位数是:(4+5)÷2=4.5(首),
故答案为:4.5首;
(2)大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有:1200×=850(人),
答:大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有850人;
(3)活动启动之初的中位数是4.5首,众数是4首,
大赛比赛后一个月时的中位数是6首,众数是6首,
由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想.
