16.2二次根式的乘除(第1课时)
图片预览




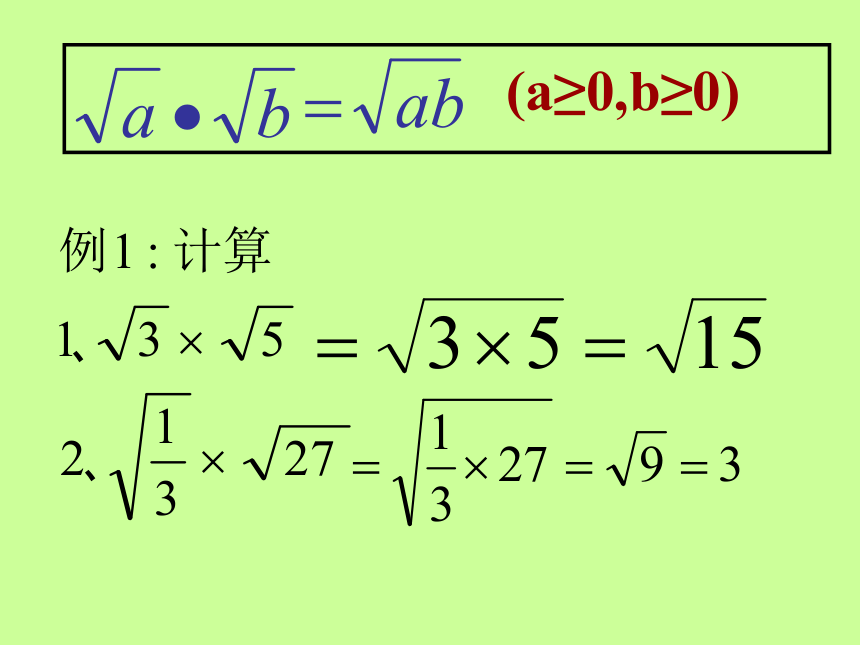


文档简介
1.什么叫二次根式?
2.两个基本性质:
温故知新
=a
a (a≥ 0)
-a (a<0)
=
=∣a∣
(a≥ 0)
计算下列各式, 观察计算结果,你发现什么规律
思考:
合作学习 自主探究
6
6
20
20
=
=
你能猜想
二次根式
乘法规定
组内合作
交流完成
a、b必须都是非负数!
(a≥0,b≥0)
语言叙述:两个二次根式相乘,把被开方数相乘,根指数不变。
(a≥0,b≥0)
分层练习:组内第3、4名学生板演
反过来:
两个非负数的积的算术平方根等于这两个数
的算术平方根的积。
(a≥0,b≥0)
1.化简:
(1) (2)
(3) (4)
分层练习:组长找学生板演
想一想?
非
负
数
合作探究:
例题3 计算:
同学们自己来算吧!
看谁算得既快又准确!
化简二次根式的步骤:
1.将被开方数尽可能分解成几个平方数.
综合提升
1.化简(直接说出结果):
体验成功的感觉!
目标检测
2、已知一个矩形的长和宽分别是
求这个矩形的面积。
本节课你有哪些收获?
各抒己见
1.本节课学习了算术平方根的积和积的算术平方根。
a≥0,b≥0
1.将被开方数尽可能分解成几个平方数.
2.化简二次根式的步骤:
( )
A.
D.
C.
B.
12
一、选择:
1.计算
B
2.已知 ,用含有a、b
的代数式表示 这个代数式为( )
A.a+b B.ab C.2a D.2b
B
当堂检测
3.下列运算正确的是 [ ]
A.
B.
C.
D.
D
5、(2009·新疆)若 ,
则xy的值是( ).
6、(2012广东)计算
的结果是 .
7、(2012青岛市)
挑战,我更行!
那么求 的值:
8、 如果下式成立
挑战无极限
的成立的条件是
必做题:
1、课本P7 1, 2, 3
2.两个基本性质:
温故知新
=a
a (a≥ 0)
-a (a<0)
=
=∣a∣
(a≥ 0)
计算下列各式, 观察计算结果,你发现什么规律
思考:
合作学习 自主探究
6
6
20
20
=
=
你能猜想
二次根式
乘法规定
组内合作
交流完成
a、b必须都是非负数!
(a≥0,b≥0)
语言叙述:两个二次根式相乘,把被开方数相乘,根指数不变。
(a≥0,b≥0)
分层练习:组内第3、4名学生板演
反过来:
两个非负数的积的算术平方根等于这两个数
的算术平方根的积。
(a≥0,b≥0)
1.化简:
(1) (2)
(3) (4)
分层练习:组长找学生板演
想一想?
非
负
数
合作探究:
例题3 计算:
同学们自己来算吧!
看谁算得既快又准确!
化简二次根式的步骤:
1.将被开方数尽可能分解成几个平方数.
综合提升
1.化简(直接说出结果):
体验成功的感觉!
目标检测
2、已知一个矩形的长和宽分别是
求这个矩形的面积。
本节课你有哪些收获?
各抒己见
1.本节课学习了算术平方根的积和积的算术平方根。
a≥0,b≥0
1.将被开方数尽可能分解成几个平方数.
2.化简二次根式的步骤:
( )
A.
D.
C.
B.
12
一、选择:
1.计算
B
2.已知 ,用含有a、b
的代数式表示 这个代数式为( )
A.a+b B.ab C.2a D.2b
B
当堂检测
3.下列运算正确的是 [ ]
A.
B.
C.
D.
D
5、(2009·新疆)若 ,
则xy的值是( ).
6、(2012广东)计算
的结果是 .
7、(2012青岛市)
挑战,我更行!
那么求 的值:
8、 如果下式成立
挑战无极限
的成立的条件是
必做题:
1、课本P7 1, 2, 3
