[七年级下册满分冲刺学案单元测试卷]第六章 频率初步(提高卷)
文档属性
| 名称 | [七年级下册满分冲刺学案单元测试卷]第六章 频率初步(提高卷) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-15 08:20:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级下册单元测试卷《第6章概率初步》提高卷
选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的.
下列成语描述的事件中,属于随机事件的是( )
A.水中捞月 B.风吹草动 C.一手遮天 D.守株待兔
2、关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率;
B.当实验次数很大时,频率稳定在概率附近;
C.当实验次数很大时,概率稳定在频率附近;
D.实验得到的频率与概率不可能相等
3、下列事件中,是不确定事件的是( )
A.打开电视正在播放重庆卫视电视台
B.同位角相等,两条直线平行
C.平行于同一条直线的两条直线平行
D.对顶角相等
4、“若ab>0,则a>0且b>0”这一事件是( )
A.必然事件 B.不确定事件 C.不可能事件 D.以上答案都不对
5、通过大量重复抛掷两枚均匀硬币的试验,出现两个反面的成功率大约稳定在( )A.25% B.50% C.75% D.100%
6、从甲,乙,丙三人中任选两名代表,甲被选中的可能性是( )
A. B. C. D.1
7、如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则( )
A.P1>P2 B.P1<P2 C.P1=P2 D.以上都有可能
8、一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来的情况下,为估计白球
的个数,小刚向其中放入8个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放入
盒中,不断重复,共摸球400次,其中88次摸到黑球,估计盒中大约有白球( )
A.28个 B.30个 C.36个 D.42个
如图,在正方体的表面展开图中,要将-a、-b、-c填入剩下的三个空白处,(彼此不同),则正方体三组相对的两个面中数字和均为零的概率为( )
B. C. D.
在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为( )
B. C. D.
填空题(本大题6小题,每小题4分,共24分)
“种瓜得瓜,种豆得豆”这一事件是 _______________.(填“必然事件”、“不可能事件”或“随机事件”).
把一转盘先分成两个半圆,再把其中一个半圆等分成三等份,并标上数字如图所示,任意转动转盘,当转盘停止时,指针落在偶数区域的概率是________.
13、有4根细木棒,它们的长度分别是3cm,4cm,5cm,7cm,从中任取3根恰好能搭成一个三角形的概率是________.
14、现有标号分别为1、2、3、4、5、6、7、8、9、10的十张卡片供甲、乙两人玩一种游戏:甲先取一张,记下点数,放回后乙再取一张,记下点数.如果取出点数为偶数就算甲胜,取出点数为3的倍数就算乙胜.并判断这种游戏规则______________(填“公平”或“不公平”)
15、初一(5)班有学生37人,其中4个或4个以上学生在同一个月出生的可能性用百分数表示为________%.
某航班每次约有100名乘客.一次飞行中飞机失事的概率为p=,一家保险公司要为乘客保险,许诺飞机一旦失事,向每位乘客赔偿60万人民币.平均来说,保险公司至少应该收取保险费________元每人.
三、解答题(一)(本大题共3题,每小题6分,共18分)
17、一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出一个球:
(1)该球是白球; (2)该球是黄球; (3)该球是红球.
估计上述事件发生的可能性的大小,将这些事件的序号按发生的可能性从小到大的顺序排列.
请你设计一个有红、白、蓝三种颜色的转盘,使得它停止转动时,指针落在红色区域的可能性比落在白色区域的可能性小,而比落在蓝色区域的可能性大.
19、投掷一枚普通的正方体骰子24次.
(1)你认为下列四种说法哪种是正确的?
①出现1点的概率等于出现3点的概率;
②投掷24次,2点一定会出现4次;
③投掷前默念几次“出现4点”,投掷结果出现4点的可能性就会加大;
④连续投掷6次,出现的点数之和不可能等于37.
(2)求出现5点的概率;
(3)出现6点大约有多少次?
四、解答答题(二)(本大题共3题,每小题7分,共21分)
20、从1,2,3这三个数字中任意取出一个、两个或三个可以构成不同的一位数、两位数或三位数,所有这些数中均无重复数字(如22,311等为有重复数字的数).
(1)列举所有可能出现的结果;
(2)出现奇数的概率是多少?
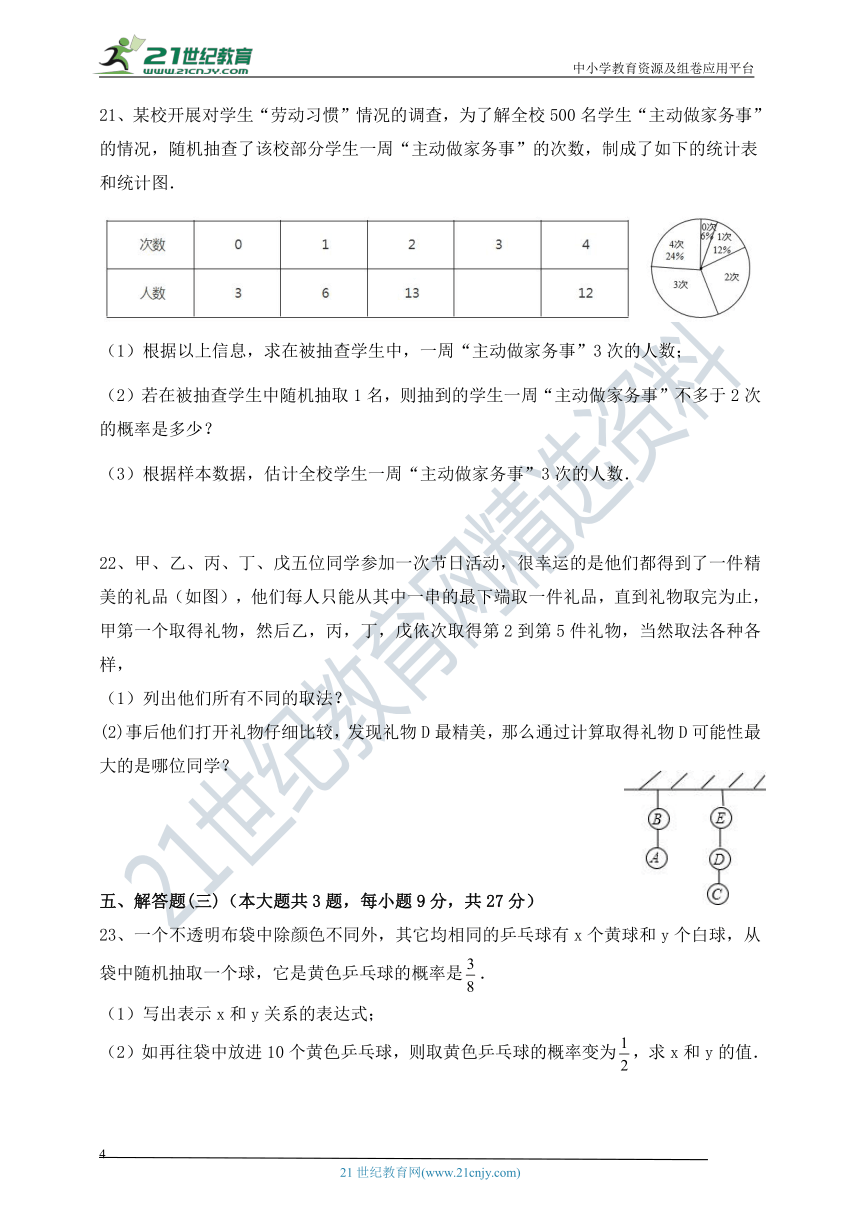
21、某校开展对学生“劳动习惯”情况的调查,为了解全校500名学生“主动做家务事”的情况,随机抽查了该校部分学生一周“主动做家务事”的次数,制成了如下的统计表和统计图.
(1)根据以上信息,求在被抽查学生中,一周“主动做家务事”3次的人数;
(2)若在被抽查学生中随机抽取1名,则抽到的学生一周“主动做家务事”不多于2次的概率是多少?
(3)根据样本数据,估计全校学生一周“主动做家务事”3次的人数.
甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙,丙,丁,戊依次取得第2到第5件礼物,当然取法各种各样,
列出他们所有不同的取法?
(2)事后他们打开礼物仔细比较,发现礼物D最精美,那么通过计算取得礼物D可能性最大的是哪位同学?
五、解答题(三)(本大题共3题,每小题9分,共27分)
23、一个不透明布袋中除颜色不同外,其它均相同的乒乓球有x个黄球和y个白球,从袋中随机抽取一个球,它是黄色乒乓球的概率是.
(1)写出表示x和y关系的表达式;
(2)如再往袋中放进10个黄色乒乓球,则取黄色乒乓球的概率变为,求x和y的值.
24、密码锁有三个转轮,每个转轮上有十个数字:0,1,2,…9.小黄同学是9月份中旬出生,用生日“月份+日期”设置密码:9××(注:中旬为某月中的11日-20日),小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是_______.
请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率.
25、甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
参考答案:
1、解:A、水中捞月是不可能事件,故A错误;
B、风吹草动是必然事件,故B错误;
C、一手遮天是不可能事件,故C错误;
D、守株待兔是随机事件,故D正确;
故选:D.
2、解:A、频率只能估计概率;
B、正确;
C、概率是定值;
D、可以相同,如“抛硬币实验”,可得到正面向上的频率为0.5,与概率相同.
故选:B.
3、解: A、打开电视正在播放重庆卫视电视台是随机事件,即:不确定事件;
B、同位角相等,两条直线平行,是必然事件,即:确定是件;
C、平行于同一条直线的两条直线平行,是必然事件,即:确定是件;
D、对顶角相等,是必然事件,即:确定是件;
故选:A.
4、解:若ab>0,则a>0且b>0,或a<0且b<0.
因而“若ab>0,则a>0且b>0”这一事件是不确定事件.
故选:B.
5、解:抛掷两枚均匀的硬币,可能出现的情况为:正正,反反,正反,反正,
∴出现两个反面的概率为,
∴抛掷多次以后,出现两个反面的成功率大约稳定在25%.
故选:A.
6、解:选两名代表共有以下情况:甲,乙;甲,丙;乙,丙;三种情况.故甲被选中的可能性是
故选:C.
7、解:由图甲可知,黑色方砖6块,共有16块方砖,
∴黑色方砖在整个地板中所占的比值==,
∴在甲种地板上最终停留在黑色区域的概率为P1是,
由图乙可知,黑色方砖3块,共有9块方砖,
∴黑色方砖在整个地板中所占的比值==,
∴在乙种地板上最终停留在黑色区域的概率为P2是,
∵>,
∴P1>P2;
故选:A.
8、解:设袋中有x个白球,根据题意得:,解之得,
故选:A.
9、解:将-a、-b、-c分别填入三个空,共有3×2×1=6种情况,其中三组相对的两个面中数字和均为零的情况只有一种,故其概率为:.
故选:D.
10、解:可以找到4个恰好能使△ABC的面积为1的点,
则概率为:.
故选:C.
11、解:“种瓜得瓜,种豆得豆”这一事件是必然事件,
故答案为:必然事件.
12、解:观察这个图可知:所标数字为偶数的面积占总面积的()=,
故其概率为.
13、解:根据题意,从有4根细木棒中任取3根,有3、4、5,3、4、7,3、5、7,4、5、7,共4种取法,
而能搭成一个三角形的有3、4、5,3、5、7,4、5、7,三种;
故其概率为 .
14、解:1、2、3、4、5、6、7、8、9、10的十张卡片中偶数的有2、4、6、8、10共5张,3的倍数有3、6、9共3张,它们可能性不相等,所以不公平.
15、解:∵一年有12个月,把37个平均分到12个月中=3…1,
∴剩下那一个无论怎么放都使那个月里超过4人.
故答案为:100%.
16、解:每次约有100名乘客,如飞机一旦失事,每位乘客赔偿60万人民币,共计6000万元,一次飞行中飞机失事的概率为P=0.00005,
故赔偿的钱数为60000000×0.00005=3000元,
故至少应该收取保险费每人==30元.
17、解:∵不透明的袋子中装有1个白球、2个黄球和3个红球,
∴摸到白球的概率为,摸到黄球的概率为,摸到红球的概率为,
∵,∴(1)<(2)<(3).
18、解:如图:白色区域的扇形面积最大,蓝色区域的扇形面积最小.
19、解:(1)
①抛掷正方体骰子出现3和出现1的概率均为,故①正确;
②投掷24次,2点不一定会出现,故②错误;
③投掷结果出现4点的概率一定,不会受主观原因改变,故③错误;
④连续投掷6次,最多为6×6=36,所以出现的点数之和不可能等于37,故④正确.
所以只有①④说法正确;
(2)出现5点的概率不受抛掷次数的影响,始终是 ;
(3)出现6点大约有24× =4次.
20、解:(1)所有可能出现的结果:一位数3个:1、2、3;两位数6个:12、13、21、23、31、32;三位数6个:123、132、213、231、312、321;
(2)共有15个数,奇数有10个,所以出现奇数的概率为.
21、解:(1)6÷12%=50(人),50-(3+6+13+12)=16(人).
答:一周“主动做家务事”3次的人数是16人;
(2)(3+6+13)÷50=22÷50=0.44.
答:抽到的学生一周“主动做家务事”不多于2次的概率是0.44;
(3)500× =160(人).
答:估计全校学生一周“主动做家务事”3次的人数是160人.
22、解:甲乙丙丁戊取礼物的顺序有10种,为:
①A、B、C、D、E;
②A、C、D、E、B;
③A、C、D、B、E;
④A、C、B、D、E;
⑤C、D、E、A、B;
⑥C、D、A、B、E;
⑦C、D、A、E、B;
⑧C、A、B、D、E;
⑨C、A、D、B、E;
⑩C、A、D、E、B.
取得礼物D的概率分别为:P(乙)=0.3,P(丙)=0.4,P(丁)=0.3,
取得礼物D可能性最大的是丙同学.
23、解:(1)∵有x个黄球和y个白球,从袋中随机抽取一个球,它是黄色乒乓球的概率是,∴,∴x=;
(2)∵再往袋中放进10个黄色乒乓球,则取黄色乒乓球的概率变为,
∴,
由(1)得x=y,把x=y代入得:y=25, ∴x=15.
24、解:(1)∵小黄同学是9月份中旬出生
∴第一个转轮设置的数字是9,第二个转轮设置的数字可能是1,2;
故答案为1或2;
(2)所有可能的密码是:911,912,913,914,915,916,917,918,919,920;
能被3整除的有912,915,918,;
密码数能被3整除的概率.
25、解:(1)若甲先摸,共有15张卡片可供选择,其中写有“石头”的卡片共3张,
故甲摸出“石头”的概率为;
(2)若甲先摸且摸出“石头”,则可供乙选择的卡片还有14张,其中乙只有摸出卡片“锤子”或“布”才能获胜,
这样的卡片共有8张,故乙获胜的概率为;
(3)若甲先摸,则“锤子”、“石头”、“剪子”、“布”四种卡片都有可能被摸出,
若甲先摸出“锤子”,则甲获胜(即乙摸出“石头”或“剪子”)的概率为;
若甲先摸出“石头”,则甲获胜(即乙摸出“剪子”)的概率为;
若甲先摸出“剪子”,则甲获胜(即乙摸出“布”)的概率为;
若甲先摸出“布”,则甲获胜(即乙摸出“锤子”或“石头”)的概率为.
故甲先摸出“锤子”获胜的可能性最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
