2.2.1 用样本的频率分布估计总体的分布 课件(27张PPT)
文档属性
| 名称 | 2.2.1 用样本的频率分布估计总体的分布 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 773.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-15 00:00:00 | ||
图片预览





文档简介
§2.2.1 用样本的频率分布
估计总体的分布
高中数学人教A版必修3
情境引入
Company Logo
情境引入
比喻只看到事物的一部分,指所见不全面或略有所得。
比喻看到的只是一部分,即可以从观察的部分推测到全貌。
用样本估计总体
管中窥豹,可见一斑
窥一斑而知全豹
探究任务
一:频数分布直方图中的组距与组数是由什么决定的?
二:频数分布直方图中的纵坐标表示什么?
三:所有小长方形的面积之和等于多少?
四:改变组距,对图中小矩形的高度有没有较大影响?
用样本的频率分布估计总体的分布
例1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水阶梯收费,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。
假设通过抽样,我们获得了100位居民某年的月平均用水量(单位:t)。
,
用样本的频率分布估计总体的分布
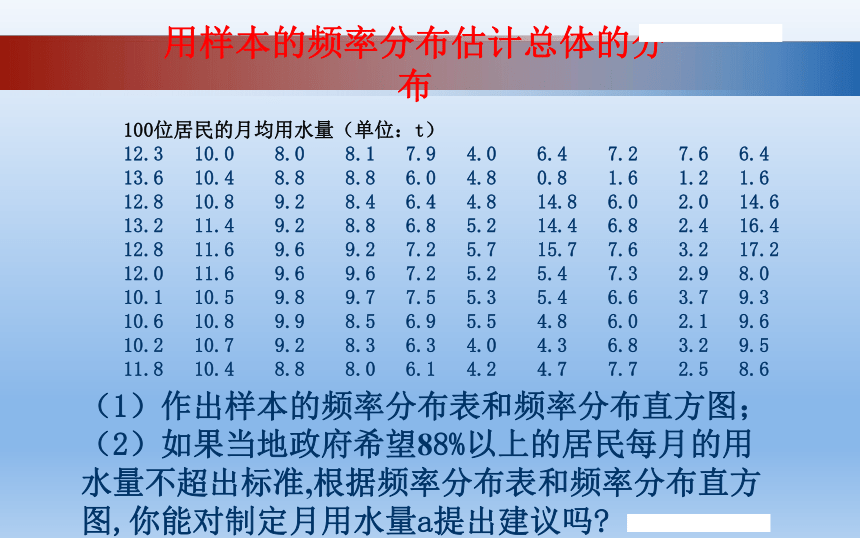
(1)作出样本的频率分布表和频率分布直方图;(2)如果当地政府希望88%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量a提出建议吗?
100位居民的月均用水量(单位:t)
12.3 10.0 8.0 8.1 7.9 4.0 6.4 7.2 7.6 6.4
13.6 10.4 8.8 8.8 6.0 4.8 0.8 1.6 1.2 1.6
12.8 10.8 9.2 8.4 6.4 4.8 14.8 6.0 2.0 14.6
13.2 11.4 9.2 8.8 6.8 5.2 14.4 6.8 2.4 16.4
12.8 11.6 9.6 9.2 7.2 5.7 15.7 7.6 3.2 17.2
12.0 11.6 9.6 9.6 7.2 5.2 5.4 7.3 2.9 8.0
10.1 10.5 9.8 9.7 7.5 5.3 5.4 6.6 3.7 9.3
10.6 10.8 9.9 8.5 6.9 5.5 4.8 6.0 2.1 9.6
10.2 10.7 9.2 8.3 6.3 4.0 4.3 6.8 3.2 9.5
11.8 10.4 8.8 8.0 6.1 4.2 4.7 7.7 2.5 8.6
频率分布直方图
一、作频率
分布直方图
的步骤
5.画频率分布直方图
1.求极差
2.决定组数与组距
3.将数据分组
4.列频率分布表
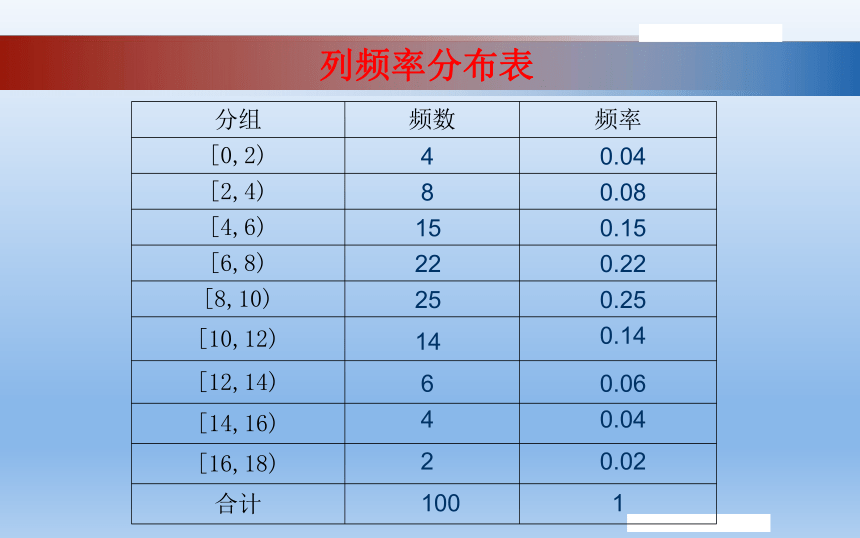
列频率分布表
分组 频数 频率
[0,2)
[2,4)
[4,6)
[6,8)
[8,10)
[10,12)
[12,14)
[14,16)
[16,18)
合计
4
0.04
8
0.08
15
22
0.22
25
0.25
14
0.14
6
0.06
4
0.04
2
0.02
100
1
0.15
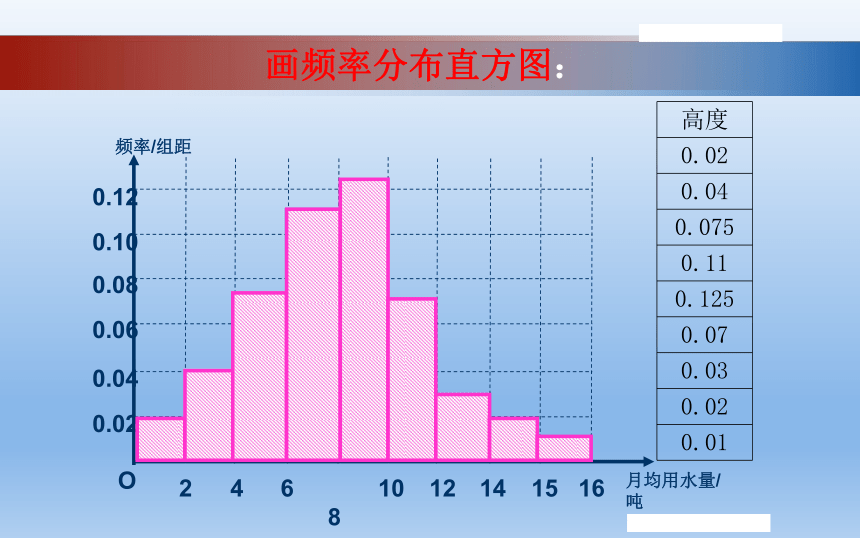
画频率分布直方图:
O
2
4
8
6
10
12
15
14
16
0.02
0.04
0.06
0.08
0.10
0.12
频率/组距
月均用水量/吨
高度
0.02
0.04
0.075
0.11
0.125
0.07
0.03
0.02
0.01
绘制频率分布直方图注意事项
注意:
1.纵坐标不是频率,而是频率/组距;
2.小矩形的面积表示频率;
3.所有小长方形的面积之和等于1;
4.可以依据样本数据的频率分布直方图估计得出总体分布的特征;
5.频率分布直方图直观的表示分布的形状,但原始的数据不能在图中表示出来。
用样本的频率分布估计总体的分布
(1)作出样本的频率分布表和频率分布直方图;(2)如果当地政府希望88%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量a提出建议吗?
100位居民的月均用水量(单位:t)
12.3 10.0 8.0 8.1 7.9 4.0 6.4 7.2 7.6 6.4
13.6 10.4 8.8 8.8 6.0 4.8 0.8 1.6 1.2 1.6
12.8 10.8 9.2 8.4 6.4 4.8 14.8 6.0 2.0 14.6
13.2 11.4 9.2 8.8 6.8 5.2 14.4 6.8 2.4 16.4
12.8 11.6 9.6 9.2 7.2 5.7 15.7 7.6 3.2 17.2
12.0 11.6 9.6 9.6 7.2 5.2 5.4 7.3 2.9 8.0
10.1 10.5 9.8 9.7 7.5 5.3 5.4 6.6 3.7 9.3
10.6 10.8 9.9 8.5 6.9 5.5 4.8 6.0 2.1 9.6
10.2 10.7 9.2 8.3 6.3 4.0 4.3 6.8 3.2 9.5
11.8 10.4 8.8 8.0 6.1 4.2 4.7 7.7 2.5 8.6
列频率分布表
分组 频数 频率
[0,2)
[2,4)
[4,6)
[6,8)
[8,10)
[10,12)
[12,14)
[14,16)
[16,18)
合计
4
0.04
8
0.08
15
22
0.22
25
0.25
14
0.14
6
0.06
4
0.04
2
0.02
100
1
0.15
例2:某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图.根据频率分布直方图推测,这3000名学生在该次数学
考试中成绩小于
60分的学生数
是 。
二、用频率分布直方图估计总体分布:
600
0.02
0.06
0.12
思维提升:
练习1:某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
(1)求出表中字母x、m、n、M所对应的数值;
(2)画出频率
分布直方图;
(3)估计该校
高一女生身
高在149.5~
165.5 cm范围
内有多少人?
0.02
0.03
0.04
0.05
0.07
思维提升:练习1
O
145.5
149.5
153.5
频率/组距
身高(cm)
157.5
161.5
165.5
169.5
思维提升:
练习1:某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
(1)求出表中字母x、m、n、M所对应的数值;
(2)画出频率
分布直方图;
(3)估计该校
高一女生身
高在149.5~
165.5 cm范围
内有多少人?
用频率分布直方图估计总体分布的注意事项
注意:
用样本估计得到的数据与真实值之间可能存在偏差,因此在实践中,对统计结论是需要进行评价的。
探究任务
一:频数分布直方图中的组距与组数是由什么决定的?
二:频数分布直方图中的纵坐标表示什么?
三:所有小长方形的面积之和等于多少?
四:改变组距,对图中小矩形的高度有没有较大影响?
三、频率分布折线图和总体密度曲线
1.频率分布折线图:连结频率分布直方图中各小长方形上端的 ,就得到频率分布折线图.
中点
频率分布折线图和总体密度曲线
2.总体密度曲线:随着 的增加,作图时 增加, 减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线。
样本容量
所分的组数
组距
频率分布折线图和总体密度曲线
2.总体密度曲线:随着 的增加,作图时 增加, 减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线。
月均用水量/吨
频率/组距
总体密度曲线
样本容量
所分的组数
组距
图中阴影部分的面积,就是总体在区间(a,b)内取值的百分比。
知识小结
绘制频率分布直方图的步骤
1
如何用频率分布直方图估计总体分布
2
频率分布折线图和总体密度曲线定义
3
当堂检测:
1.一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000](元)月收入段应抽出 人
25
当堂检测:
2.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;……第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )A.0.9,35 B.0.9,45
C.0.1,35 D.0.1,45
A
当堂检测:
3.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下,根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 ( )
(A)20 (B)30 (C)40 (D)50
C
当堂检测:
4.有一个容量为50的样本数据的分组及各组的频数如下:
[12.5, 15.5) 3 [15.5, 18.5) 8 [18.5, 21.5) 9 [21.5, 24.5) 11 [24.5, 27.5) 10 [27.5, 30.5) 5
[30.5, 33.5) 4
⑴列出样本的频率分布表和画出频率分布直方图;
⑵根据样本的频率分布估计,小于30.5的数据约占多少?
课下作业:《习案》作业十八
Thank You !
估计总体的分布
高中数学人教A版必修3
情境引入
Company Logo
情境引入
比喻只看到事物的一部分,指所见不全面或略有所得。
比喻看到的只是一部分,即可以从观察的部分推测到全貌。
用样本估计总体
管中窥豹,可见一斑
窥一斑而知全豹
探究任务
一:频数分布直方图中的组距与组数是由什么决定的?
二:频数分布直方图中的纵坐标表示什么?
三:所有小长方形的面积之和等于多少?
四:改变组距,对图中小矩形的高度有没有较大影响?
用样本的频率分布估计总体的分布
例1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水阶梯收费,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。
假设通过抽样,我们获得了100位居民某年的月平均用水量(单位:t)。
,
用样本的频率分布估计总体的分布
(1)作出样本的频率分布表和频率分布直方图;(2)如果当地政府希望88%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量a提出建议吗?
100位居民的月均用水量(单位:t)
12.3 10.0 8.0 8.1 7.9 4.0 6.4 7.2 7.6 6.4
13.6 10.4 8.8 8.8 6.0 4.8 0.8 1.6 1.2 1.6
12.8 10.8 9.2 8.4 6.4 4.8 14.8 6.0 2.0 14.6
13.2 11.4 9.2 8.8 6.8 5.2 14.4 6.8 2.4 16.4
12.8 11.6 9.6 9.2 7.2 5.7 15.7 7.6 3.2 17.2
12.0 11.6 9.6 9.6 7.2 5.2 5.4 7.3 2.9 8.0
10.1 10.5 9.8 9.7 7.5 5.3 5.4 6.6 3.7 9.3
10.6 10.8 9.9 8.5 6.9 5.5 4.8 6.0 2.1 9.6
10.2 10.7 9.2 8.3 6.3 4.0 4.3 6.8 3.2 9.5
11.8 10.4 8.8 8.0 6.1 4.2 4.7 7.7 2.5 8.6
频率分布直方图
一、作频率
分布直方图
的步骤
5.画频率分布直方图
1.求极差
2.决定组数与组距
3.将数据分组
4.列频率分布表
列频率分布表
分组 频数 频率
[0,2)
[2,4)
[4,6)
[6,8)
[8,10)
[10,12)
[12,14)
[14,16)
[16,18)
合计
4
0.04
8
0.08
15
22
0.22
25
0.25
14
0.14
6
0.06
4
0.04
2
0.02
100
1
0.15
画频率分布直方图:
O
2
4
8
6
10
12
15
14
16
0.02
0.04
0.06
0.08
0.10
0.12
频率/组距
月均用水量/吨
高度
0.02
0.04
0.075
0.11
0.125
0.07
0.03
0.02
0.01
绘制频率分布直方图注意事项
注意:
1.纵坐标不是频率,而是频率/组距;
2.小矩形的面积表示频率;
3.所有小长方形的面积之和等于1;
4.可以依据样本数据的频率分布直方图估计得出总体分布的特征;
5.频率分布直方图直观的表示分布的形状,但原始的数据不能在图中表示出来。
用样本的频率分布估计总体的分布
(1)作出样本的频率分布表和频率分布直方图;(2)如果当地政府希望88%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量a提出建议吗?
100位居民的月均用水量(单位:t)
12.3 10.0 8.0 8.1 7.9 4.0 6.4 7.2 7.6 6.4
13.6 10.4 8.8 8.8 6.0 4.8 0.8 1.6 1.2 1.6
12.8 10.8 9.2 8.4 6.4 4.8 14.8 6.0 2.0 14.6
13.2 11.4 9.2 8.8 6.8 5.2 14.4 6.8 2.4 16.4
12.8 11.6 9.6 9.2 7.2 5.7 15.7 7.6 3.2 17.2
12.0 11.6 9.6 9.6 7.2 5.2 5.4 7.3 2.9 8.0
10.1 10.5 9.8 9.7 7.5 5.3 5.4 6.6 3.7 9.3
10.6 10.8 9.9 8.5 6.9 5.5 4.8 6.0 2.1 9.6
10.2 10.7 9.2 8.3 6.3 4.0 4.3 6.8 3.2 9.5
11.8 10.4 8.8 8.0 6.1 4.2 4.7 7.7 2.5 8.6
列频率分布表
分组 频数 频率
[0,2)
[2,4)
[4,6)
[6,8)
[8,10)
[10,12)
[12,14)
[14,16)
[16,18)
合计
4
0.04
8
0.08
15
22
0.22
25
0.25
14
0.14
6
0.06
4
0.04
2
0.02
100
1
0.15
例2:某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图.根据频率分布直方图推测,这3000名学生在该次数学
考试中成绩小于
60分的学生数
是 。
二、用频率分布直方图估计总体分布:
600
0.02
0.06
0.12
思维提升:
练习1:某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
(1)求出表中字母x、m、n、M所对应的数值;
(2)画出频率
分布直方图;
(3)估计该校
高一女生身
高在149.5~
165.5 cm范围
内有多少人?
0.02
0.03
0.04
0.05
0.07
思维提升:练习1
O
145.5
149.5
153.5
频率/组距
身高(cm)
157.5
161.5
165.5
169.5
思维提升:
练习1:某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
(1)求出表中字母x、m、n、M所对应的数值;
(2)画出频率
分布直方图;
(3)估计该校
高一女生身
高在149.5~
165.5 cm范围
内有多少人?
用频率分布直方图估计总体分布的注意事项
注意:
用样本估计得到的数据与真实值之间可能存在偏差,因此在实践中,对统计结论是需要进行评价的。
探究任务
一:频数分布直方图中的组距与组数是由什么决定的?
二:频数分布直方图中的纵坐标表示什么?
三:所有小长方形的面积之和等于多少?
四:改变组距,对图中小矩形的高度有没有较大影响?
三、频率分布折线图和总体密度曲线
1.频率分布折线图:连结频率分布直方图中各小长方形上端的 ,就得到频率分布折线图.
中点
频率分布折线图和总体密度曲线
2.总体密度曲线:随着 的增加,作图时 增加, 减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线。
样本容量
所分的组数
组距
频率分布折线图和总体密度曲线
2.总体密度曲线:随着 的增加,作图时 增加, 减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线。
月均用水量/吨
频率/组距
总体密度曲线
样本容量
所分的组数
组距
图中阴影部分的面积,就是总体在区间(a,b)内取值的百分比。
知识小结
绘制频率分布直方图的步骤
1
如何用频率分布直方图估计总体分布
2
频率分布折线图和总体密度曲线定义
3
当堂检测:
1.一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000](元)月收入段应抽出 人
25
当堂检测:
2.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;……第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )A.0.9,35 B.0.9,45
C.0.1,35 D.0.1,45
A
当堂检测:
3.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下,根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 ( )
(A)20 (B)30 (C)40 (D)50
C
当堂检测:
4.有一个容量为50的样本数据的分组及各组的频数如下:
[12.5, 15.5) 3 [15.5, 18.5) 8 [18.5, 21.5) 9 [21.5, 24.5) 11 [24.5, 27.5) 10 [27.5, 30.5) 5
[30.5, 33.5) 4
⑴列出样本的频率分布表和画出频率分布直方图;
⑵根据样本的频率分布估计,小于30.5的数据约占多少?
课下作业:《习案》作业十八
Thank You !
