2.2.2 用样本的数字特征估计总体的数字特征 课件(28张PPT)
文档属性
| 名称 | 2.2.2 用样本的数字特征估计总体的数字特征 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-15 10:07:22 | ||
图片预览








文档简介
2.2.2 用样本的数字特征估计
总体的数字特征
我们班级是双语班,大多数同学相对于平行班基础要弱一点,上课学习安排的内容相对少点,讲解比较细致,语速也比较慢,只安排了众数、中位数、平均数,在频率分布直方图下求众数、中位数、平均数是重点讲解,这节课我们将学习如何从样本中提取基本信息(众数、中位数、平均数)来推断总体的情况。
学情分析
1.对一个未知总体,我们常用样本的频率分布来估计总体的频率分布,其中表示样本数据的频率分布的基本方法有哪些.
图、表、总体数据的数字特征
新课导入
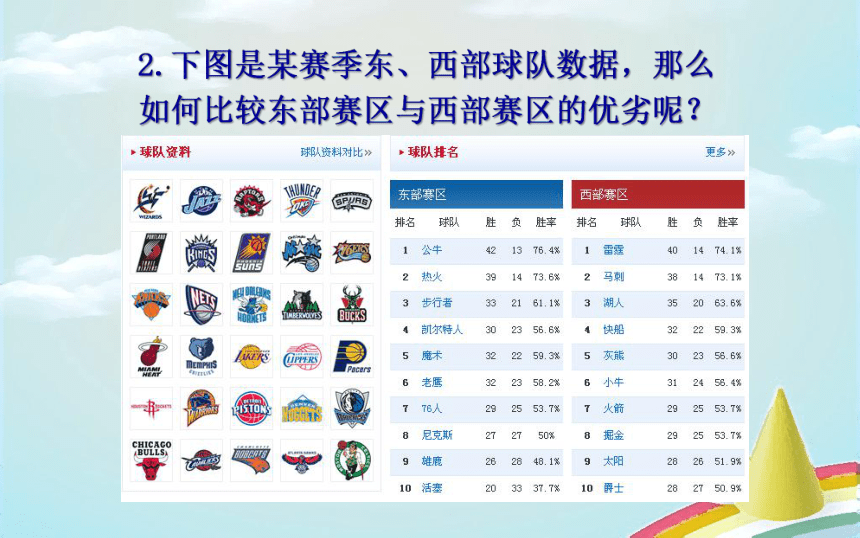
2.下图是某赛季东、西部球队数据,那么如何比较东部赛区与西部赛区的优劣呢?
1.理解用样本的基本数字特征来估计总体
的基本数字特征.(难点)
2.用相关知识来解决简单的统计问题.(重点)
3.体会样本数据特征具有随机性(重点)
学习目标
4.初步体会、领悟“用数据说话”的统计思想方法。
【教学方法】:启发式、探究式
1.众数的定义: 在一组数据中,出现次数最多的数据叫做这一组数据的众数.
2.中位数的定义: 将一组数据按大小顺序依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
3.平均数的定义:一组数据的和除以数据的个数所得到的数.
复习回顾
求下列一组数的众数、中位数、平均数
(1)2,2,3,3,5,6,7
(2)2,3,5,5
小练习
判一判(正确的打“√”,错误的打“×”)
(1)中位数一定是样本数据中的某个数.( )
(2)在一组样本数据中,众数一定是唯一的.( )
众数可以有多个,中位数是唯一的.
(求中位数先排序)
×
×
(3)10名工人生产同一零件的件数是5, 8, 4, 10, 7, 6, 8, 8, 5, 9.平均数为a, 中位数为b,众数为c.则( )
A. c>b>a, B. b>c>a,
C. a>b>c, D. c>a>b
A
想一想:
在频率分布直方图中,我们怎样找众数、中位数、平均数?
月均用水量/t
频率/组距
0.50
0.40
0.30
0.20
0.10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
O
取最高矩形下端中点的横坐标2.25作为众数.
思考1:在城市居民月均用水量样本数据的频率分布直方图中,你认为众数应在哪个小矩形内?由此估计总体的众数是什么?
注意:哪段范围的数最多?
由直方图看出众数是2.25,可是抽样的数据中没有2.25,为什么区间的中点值2.25是众数呢?
因为样本数据的频率分布直方图把原始数据遗失,是用中点值来估计的。
?
思考2:在频率分布直方图中,每个小矩形的面积表示什么?
每个小矩形的面积即为所在组的频率
中位数左右两侧的直方图的面积应有什么关系?
中位数左边和右边的直方图的面积应该相等.
S左=S右=0.5
从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.
0.5-0.04-0.08-0.15-0.22=0.01,
0.5×(0.01÷0.25)=0.02,所以中位数是2.02.
月均用水量/t
0.50
0.40
0.30
0.20
0.10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
o
频率/组距
求中位数
若你是政府决策者,为了使百分之81的居民不受影响,怎样制定用水标准合适?
考考你
月均用水量/t
频率/组距
0.50
0.40
0.30
0.20
0.10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
O
思考3:平均数是频率分布直方图的“重心”,在城市居民月均用水量样本数据的频率分布直方图中,各个小矩形的重心在哪里?从直方图估计总体在各组数据内的平均数分别为多少?
解析:根据统计学中数学期望原理,将频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数.
0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25× 0.06+3.75×0.04+4.25×0.02=2.02(t).
平均数是2.02.
平均数与中位数相等,是必然还是巧合?
思考4:从居民月均用水量样本数据可知,该样本的众数是2.3,中位数是2.0,平均数是1.973,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
频率分布直方图损失了一些样本数据,得到的是一个估计值,且所得估值与数据分组有关,有随机性.
注:在只有样本频率分布直方图的情况下,我们可以按上述方法估计众数、中位数和平均数,并由此估计总体特征.
样本的众数、中位数和平均数常用来表示样本数据的“中心值”.
1.众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息.
2.平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.
三数的优缺点
【例题】某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
求:高一参赛学生的成绩的众数、中位数、平均数.
【解析】
用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,众数为65,
又因为第一个小矩形的面积为0.3,所以设第二个小矩形底边的一部分长为x,
则x×0.04=0.2,得x=5,
所以中位数为60+5=65.
由平均数公式计算:
0.3×55+0.4×65+0.15×75+0.1×85+0.05×95=67
所以平均数为67.
1.10名工人某天生产同一零件,生产的件数分别是
15,17,14,10,15,19,17,16,14,12,则这
一天 10名工人生产的零件的中位数是( )
A.14 B.16 C.15 D.17
【解析】选C.把件数从小到大排列为10,12,14,14,15,15,16,17,17,19,可知中位数为15.
C
课堂训练
2.甲、乙两个班各随机选出
15名同学进行测验,所得成
绩的茎叶图如图.从图中看,
_____班的平均成绩较高.
【解析】结合茎叶图中成绩的情况可知,
乙班平均成绩较高.
答案:乙
3.统计某校1 000名学生的数学会考成绩,得到样本频率分布直方图如图所示,规定不低于60分为及格,不低于80分为优秀,则及格人数是______;优秀率为______.
【解析】由已知不低于60分及格,则及格的频率为0.025×10+0.035×10+0.01×20
=0.25+0.35+0.2=0.8.
所以及格的人数为1 000×0.8=800.
不低于80分为优秀,则优秀的频率为0.01×20=0.2. 所以优秀率为20%.
答案:800 20%
4.(2017·山东文,8)如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
A.3,5 B.5,5
C.3,7 D.5,7
A
1.样本的数字特征:众数、中位数和平均数.
2.用样本频率分布直方图估计样本的众数、中位数、平均数.
(1)众数规定为频率分布直方图中最高矩形下端的中点.
(2)中位数两边的直方图的面积相等.
(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数.
课堂小结
导学案后面的课后作业
布置作业
总体的数字特征
我们班级是双语班,大多数同学相对于平行班基础要弱一点,上课学习安排的内容相对少点,讲解比较细致,语速也比较慢,只安排了众数、中位数、平均数,在频率分布直方图下求众数、中位数、平均数是重点讲解,这节课我们将学习如何从样本中提取基本信息(众数、中位数、平均数)来推断总体的情况。
学情分析
1.对一个未知总体,我们常用样本的频率分布来估计总体的频率分布,其中表示样本数据的频率分布的基本方法有哪些.
图、表、总体数据的数字特征
新课导入
2.下图是某赛季东、西部球队数据,那么如何比较东部赛区与西部赛区的优劣呢?
1.理解用样本的基本数字特征来估计总体
的基本数字特征.(难点)
2.用相关知识来解决简单的统计问题.(重点)
3.体会样本数据特征具有随机性(重点)
学习目标
4.初步体会、领悟“用数据说话”的统计思想方法。
【教学方法】:启发式、探究式
1.众数的定义: 在一组数据中,出现次数最多的数据叫做这一组数据的众数.
2.中位数的定义: 将一组数据按大小顺序依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
3.平均数的定义:一组数据的和除以数据的个数所得到的数.
复习回顾
求下列一组数的众数、中位数、平均数
(1)2,2,3,3,5,6,7
(2)2,3,5,5
小练习
判一判(正确的打“√”,错误的打“×”)
(1)中位数一定是样本数据中的某个数.( )
(2)在一组样本数据中,众数一定是唯一的.( )
众数可以有多个,中位数是唯一的.
(求中位数先排序)
×
×
(3)10名工人生产同一零件的件数是5, 8, 4, 10, 7, 6, 8, 8, 5, 9.平均数为a, 中位数为b,众数为c.则( )
A. c>b>a, B. b>c>a,
C. a>b>c, D. c>a>b
A
想一想:
在频率分布直方图中,我们怎样找众数、中位数、平均数?
月均用水量/t
频率/组距
0.50
0.40
0.30
0.20
0.10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
O
取最高矩形下端中点的横坐标2.25作为众数.
思考1:在城市居民月均用水量样本数据的频率分布直方图中,你认为众数应在哪个小矩形内?由此估计总体的众数是什么?
注意:哪段范围的数最多?
由直方图看出众数是2.25,可是抽样的数据中没有2.25,为什么区间的中点值2.25是众数呢?
因为样本数据的频率分布直方图把原始数据遗失,是用中点值来估计的。
?
思考2:在频率分布直方图中,每个小矩形的面积表示什么?
每个小矩形的面积即为所在组的频率
中位数左右两侧的直方图的面积应有什么关系?
中位数左边和右边的直方图的面积应该相等.
S左=S右=0.5
从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.
0.5-0.04-0.08-0.15-0.22=0.01,
0.5×(0.01÷0.25)=0.02,所以中位数是2.02.
月均用水量/t
0.50
0.40
0.30
0.20
0.10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
o
频率/组距
求中位数
若你是政府决策者,为了使百分之81的居民不受影响,怎样制定用水标准合适?
考考你
月均用水量/t
频率/组距
0.50
0.40
0.30
0.20
0.10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
O
思考3:平均数是频率分布直方图的“重心”,在城市居民月均用水量样本数据的频率分布直方图中,各个小矩形的重心在哪里?从直方图估计总体在各组数据内的平均数分别为多少?
解析:根据统计学中数学期望原理,将频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数.
0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25× 0.06+3.75×0.04+4.25×0.02=2.02(t).
平均数是2.02.
平均数与中位数相等,是必然还是巧合?
思考4:从居民月均用水量样本数据可知,该样本的众数是2.3,中位数是2.0,平均数是1.973,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
频率分布直方图损失了一些样本数据,得到的是一个估计值,且所得估值与数据分组有关,有随机性.
注:在只有样本频率分布直方图的情况下,我们可以按上述方法估计众数、中位数和平均数,并由此估计总体特征.
样本的众数、中位数和平均数常用来表示样本数据的“中心值”.
1.众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息.
2.平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.
三数的优缺点
【例题】某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
求:高一参赛学生的成绩的众数、中位数、平均数.
【解析】
用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,众数为65,
又因为第一个小矩形的面积为0.3,所以设第二个小矩形底边的一部分长为x,
则x×0.04=0.2,得x=5,
所以中位数为60+5=65.
由平均数公式计算:
0.3×55+0.4×65+0.15×75+0.1×85+0.05×95=67
所以平均数为67.
1.10名工人某天生产同一零件,生产的件数分别是
15,17,14,10,15,19,17,16,14,12,则这
一天 10名工人生产的零件的中位数是( )
A.14 B.16 C.15 D.17
【解析】选C.把件数从小到大排列为10,12,14,14,15,15,16,17,17,19,可知中位数为15.
C
课堂训练
2.甲、乙两个班各随机选出
15名同学进行测验,所得成
绩的茎叶图如图.从图中看,
_____班的平均成绩较高.
【解析】结合茎叶图中成绩的情况可知,
乙班平均成绩较高.
答案:乙
3.统计某校1 000名学生的数学会考成绩,得到样本频率分布直方图如图所示,规定不低于60分为及格,不低于80分为优秀,则及格人数是______;优秀率为______.
【解析】由已知不低于60分及格,则及格的频率为0.025×10+0.035×10+0.01×20
=0.25+0.35+0.2=0.8.
所以及格的人数为1 000×0.8=800.
不低于80分为优秀,则优秀的频率为0.01×20=0.2. 所以优秀率为20%.
答案:800 20%
4.(2017·山东文,8)如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
A.3,5 B.5,5
C.3,7 D.5,7
A
1.样本的数字特征:众数、中位数和平均数.
2.用样本频率分布直方图估计样本的众数、中位数、平均数.
(1)众数规定为频率分布直方图中最高矩形下端的中点.
(2)中位数两边的直方图的面积相等.
(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数.
课堂小结
导学案后面的课后作业
布置作业
