2.3.1 变量间的相关关系 课件(34张PPT)
文档属性
| 名称 | 2.3.1 变量间的相关关系 课件(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-15 10:10:14 | ||
图片预览










文档简介
变量间的相关关系
学习目标:
1了解变量间的相关关系,能利用散点图 直观认识变量间的相关关系。
2理解回归直线方程的意义,能够求出回归直线方程。
3体会统计思想与确定性思维的差异。
小明,你数学成绩不太好,物理怎么样?
也不太好啊.
学不好数学,物理也是学不好的
?????...
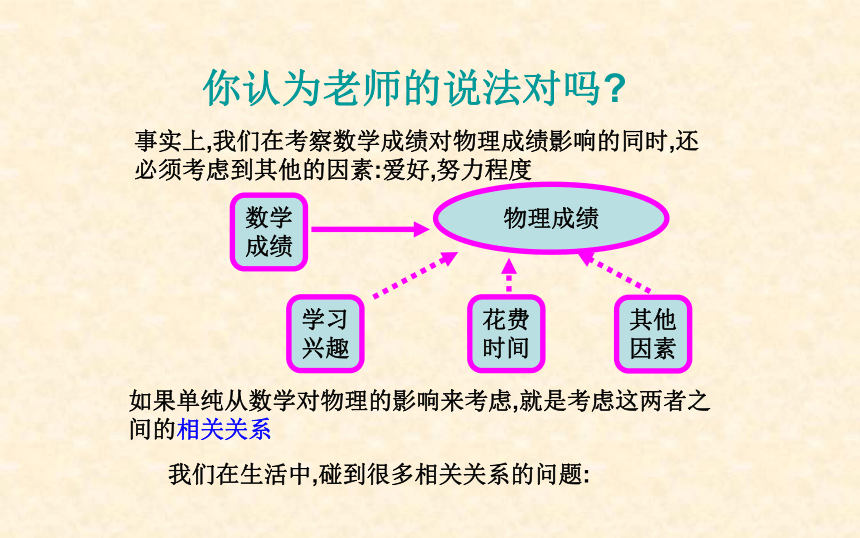
你认为老师的说法对吗?
事实上,我们在考察数学成绩对物理成绩影响的同时,还必须考虑到其他的因素:爱好,努力程度
如果单纯从数学对物理的影响来考虑,就是考虑这两者之间的相关关系
我们在生活中,碰到很多相关关系的问题:
物理成绩
数学成绩
学习兴趣
花费时间
其他因素
1〉商品销售收入与广告支出经费之间的关系。
商品销售收入与广告支出经费之间有着密切的联系,但商品收入不仅与广告支出多少有关,还与商品质量、居民收入等因素有关。
我们还可以举出现实生活中存在的许多相关关系的问题。例如:
在一定范围内,施肥量越大,粮食产量就越高。但是,施肥量并不是决定粮食产量的唯一因素,因为粮食产量还要受到土壤质量、降雨量、田间管理水平等因素的影响。
2〉粮食产量与施肥量之间的关系。
在一定年龄段内,随着年龄的增长,人体内的脂肪含量会增加,但人体内的脂肪含量还与饮食习惯、体育锻炼等有关,可能还与个人的先天体质有关。
3〉人体内脂肪含量与年龄之间的关系。
上面的几个例子都反映了:两个变量之间是一种不确定的关系。产生这种关系的原因是受到许多不确定的随机因素的影响。
当自变量取值一定,因变量的取值带有一定 随机性时,两个变量之间的关系称为相关关系。相关关系是一种不确定关系。
变量间的相关关系:
不同点:1、函数关系是一种确定的关系;而相关关系是一种非确定关系.
相关关系与函数关系的异同点:
相同点:均是指两个变量的关系.
3、函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.
2、相关关系中两个变量之间产生相关关系的原因是
受许多不确定的随机因素的影响。
1.下列关系中,是带有随机性相关关系的是 .
①正方形的边长与面积的关系;②水稻产量与施肥量之间的关系;③人的身高与年龄之间的关系;④降雪量与交通事故发生之间的关系.
②④
即学即练:
2. 下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值
B. 正方形边长和面积
C.正n边形的边数和它的内角和
D. 人的年龄和身高
D
【问题】在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据上述数据,人体的脂肪含量与年龄之间
有怎样的关系?
思考1:为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
思考2:上图叫做散点图,你能描述一下散点图的含义吗?
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
观察散点图的大致趋势, 两个变量的散点图中点的分布的位置是从左下角到右上角的区域,我们称这种相关关系为正相关。
思考3:如果两个变量成负相关,从整体上看这两个变量的变化趋势如何?
散点图中的点散布在从左上角到右下角的区域.
散点图说明
3)如果所有的样本点都落在某一直线附近,
变量之间就有线性相关关系 .
1)如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.
2)如果所有的样本点都落在某一函数曲线附近,
变量之间就有相关关系。
散点图:用来判断两个变量是否具有相关关系.
正相关
(2)吸烟有害健康
负相关
(3)高原含氧量与海拔高度
负相关
(4)学习的努力程度与学习成绩
正相关
练习:判断下列各题属于哪种相关关系?
(1)某工厂一月份总成本与该月总产量
思考:你能列举一些生活中的变量成正相关或负相关的实例吗?
1、名师出高徒
2、高瞻远瞩
3、见多识广
4、种瓜得瓜,种豆得豆
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。
这条回归直线的方程,简称为回归方程。
回归直线
整体上最接近
方案:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。
四、如何具体的求出这个回归方程呢?
根据有关数学原理分析,当
时,总体偏差 为最小,这样就得到了回归方程,这种求回归方程的方法叫做最小二乘法.回归方程
中, a, b的几何意义分别是什么?
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
脂肪含量
0
若某人65岁,可预测他体内脂肪含量在37.1%(0.577×65-0.448= 37.1%)附近的可能性比较大。
但不能说他体内脂肪含量一定是37.1%
原因:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差,即使截距斜率没有误差,也不可能百分百地保证对应于x,预报值Y能等于实际值y
例1:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
1、画出散点图;
2、从散点图中发现气温与热饮销售杯数之间关系的一般规律;
3、求回归方程;
4、如果某天的气温是2摄氏度,预测这天卖出的热饮杯数。
热氏温度/℃ 热饮杯数
-5 156
0 150
4 132
7 128
10 130
15 116
19 104
23 89
27 93
31 76
36 54
练习:给出施化肥量对水稻产量影响的
试验数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
(1)画出上表的散点图;
(2)求出回归直线并且画出图形.
从而得回归直线方程是
解:(1)散点图(略).
(2)表中的数据进行具体计算,列成以下表格
20475
18000
15575
12150
9125
6900
4950
xiyi
455
450
445
405
365
345
330
yi
45
40
35
30
25
20
15
xi
7
6
5
4
3
2
1
i
.(图形略)
故可得到
2.回归方程被样本数据惟一确定,各样本点大致分布在回归直线附近.对同一个总体,不同的样本数据对应不同的回归直线,所以回归直线也具有随机性.
3.对于任意一组样本数据,利用上述公式都可以求得“回归方程”,如果这组数据不具有线性相关关系,即不存在回归直线,那么所得的“回归方程”是没有实际意义的.因此,对一组样本数据,应先作散点图,在具有线性相关关系的前提下再求回归方程.
再见
学习目标:
1了解变量间的相关关系,能利用散点图 直观认识变量间的相关关系。
2理解回归直线方程的意义,能够求出回归直线方程。
3体会统计思想与确定性思维的差异。
小明,你数学成绩不太好,物理怎么样?
也不太好啊.
学不好数学,物理也是学不好的
?????...
你认为老师的说法对吗?
事实上,我们在考察数学成绩对物理成绩影响的同时,还必须考虑到其他的因素:爱好,努力程度
如果单纯从数学对物理的影响来考虑,就是考虑这两者之间的相关关系
我们在生活中,碰到很多相关关系的问题:
物理成绩
数学成绩
学习兴趣
花费时间
其他因素
1〉商品销售收入与广告支出经费之间的关系。
商品销售收入与广告支出经费之间有着密切的联系,但商品收入不仅与广告支出多少有关,还与商品质量、居民收入等因素有关。
我们还可以举出现实生活中存在的许多相关关系的问题。例如:
在一定范围内,施肥量越大,粮食产量就越高。但是,施肥量并不是决定粮食产量的唯一因素,因为粮食产量还要受到土壤质量、降雨量、田间管理水平等因素的影响。
2〉粮食产量与施肥量之间的关系。
在一定年龄段内,随着年龄的增长,人体内的脂肪含量会增加,但人体内的脂肪含量还与饮食习惯、体育锻炼等有关,可能还与个人的先天体质有关。
3〉人体内脂肪含量与年龄之间的关系。
上面的几个例子都反映了:两个变量之间是一种不确定的关系。产生这种关系的原因是受到许多不确定的随机因素的影响。
当自变量取值一定,因变量的取值带有一定 随机性时,两个变量之间的关系称为相关关系。相关关系是一种不确定关系。
变量间的相关关系:
不同点:1、函数关系是一种确定的关系;而相关关系是一种非确定关系.
相关关系与函数关系的异同点:
相同点:均是指两个变量的关系.
3、函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.
2、相关关系中两个变量之间产生相关关系的原因是
受许多不确定的随机因素的影响。
1.下列关系中,是带有随机性相关关系的是 .
①正方形的边长与面积的关系;②水稻产量与施肥量之间的关系;③人的身高与年龄之间的关系;④降雪量与交通事故发生之间的关系.
②④
即学即练:
2. 下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值
B. 正方形边长和面积
C.正n边形的边数和它的内角和
D. 人的年龄和身高
D
【问题】在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据上述数据,人体的脂肪含量与年龄之间
有怎样的关系?
思考1:为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
思考2:上图叫做散点图,你能描述一下散点图的含义吗?
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
观察散点图的大致趋势, 两个变量的散点图中点的分布的位置是从左下角到右上角的区域,我们称这种相关关系为正相关。
思考3:如果两个变量成负相关,从整体上看这两个变量的变化趋势如何?
散点图中的点散布在从左上角到右下角的区域.
散点图说明
3)如果所有的样本点都落在某一直线附近,
变量之间就有线性相关关系 .
1)如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.
2)如果所有的样本点都落在某一函数曲线附近,
变量之间就有相关关系。
散点图:用来判断两个变量是否具有相关关系.
正相关
(2)吸烟有害健康
负相关
(3)高原含氧量与海拔高度
负相关
(4)学习的努力程度与学习成绩
正相关
练习:判断下列各题属于哪种相关关系?
(1)某工厂一月份总成本与该月总产量
思考:你能列举一些生活中的变量成正相关或负相关的实例吗?
1、名师出高徒
2、高瞻远瞩
3、见多识广
4、种瓜得瓜,种豆得豆
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。
这条回归直线的方程,简称为回归方程。
回归直线
整体上最接近
方案:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。
四、如何具体的求出这个回归方程呢?
根据有关数学原理分析,当
时,总体偏差 为最小,这样就得到了回归方程,这种求回归方程的方法叫做最小二乘法.回归方程
中, a, b的几何意义分别是什么?
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
脂肪含量
0
若某人65岁,可预测他体内脂肪含量在37.1%(0.577×65-0.448= 37.1%)附近的可能性比较大。
但不能说他体内脂肪含量一定是37.1%
原因:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差,即使截距斜率没有误差,也不可能百分百地保证对应于x,预报值Y能等于实际值y
例1:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
1、画出散点图;
2、从散点图中发现气温与热饮销售杯数之间关系的一般规律;
3、求回归方程;
4、如果某天的气温是2摄氏度,预测这天卖出的热饮杯数。
热氏温度/℃ 热饮杯数
-5 156
0 150
4 132
7 128
10 130
15 116
19 104
23 89
27 93
31 76
36 54
练习:给出施化肥量对水稻产量影响的
试验数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
(1)画出上表的散点图;
(2)求出回归直线并且画出图形.
从而得回归直线方程是
解:(1)散点图(略).
(2)表中的数据进行具体计算,列成以下表格
20475
18000
15575
12150
9125
6900
4950
xiyi
455
450
445
405
365
345
330
yi
45
40
35
30
25
20
15
xi
7
6
5
4
3
2
1
i
.(图形略)
故可得到
2.回归方程被样本数据惟一确定,各样本点大致分布在回归直线附近.对同一个总体,不同的样本数据对应不同的回归直线,所以回归直线也具有随机性.
3.对于任意一组样本数据,利用上述公式都可以求得“回归方程”,如果这组数据不具有线性相关关系,即不存在回归直线,那么所得的“回归方程”是没有实际意义的.因此,对一组样本数据,应先作散点图,在具有线性相关关系的前提下再求回归方程.
再见
