江苏省江都区丁伙中学2018-2019学年七年级下数学第7章平面图形的认识二单元测试
文档属性
| 名称 | 江苏省江都区丁伙中学2018-2019学年七年级下数学第7章平面图形的认识二单元测试 |  | |
| 格式 | zip | ||
| 文件大小 | 305.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-15 10:28:49 | ||
图片预览

文档简介
七年级数学第7章《平面图形的认识二》同步提高测试
一、选择题:
1、(2018·南通)若一个凸多边形的内角和为720°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2、如图,AB∥DE,∠CDE=40°,则∠B的度数是( )
A.40° B.50° C.60° D.70°
3、如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
4、已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为( )
A.5 B.4 C.6 D.7
5、线段AB=5 cm,BC=2 cm,则A、C两点间的距离为 ( )
A.7 cm B.3 cm
C.7 cm或3 cm D.不小于3 cm且不大于7 cm
6、下列长度的三条线段,能组成三角形的是( )
A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cm
C.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm
7、如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D,E,F,则△ABC中BC边上的高是( )
A.CF B.BE C.AD D.CD
8、用一副三角板画角,不能画出的度数是( )
A.80° B.15° C.75° D.150°
9、如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( )
A.42° B.50° C.60° D.68°
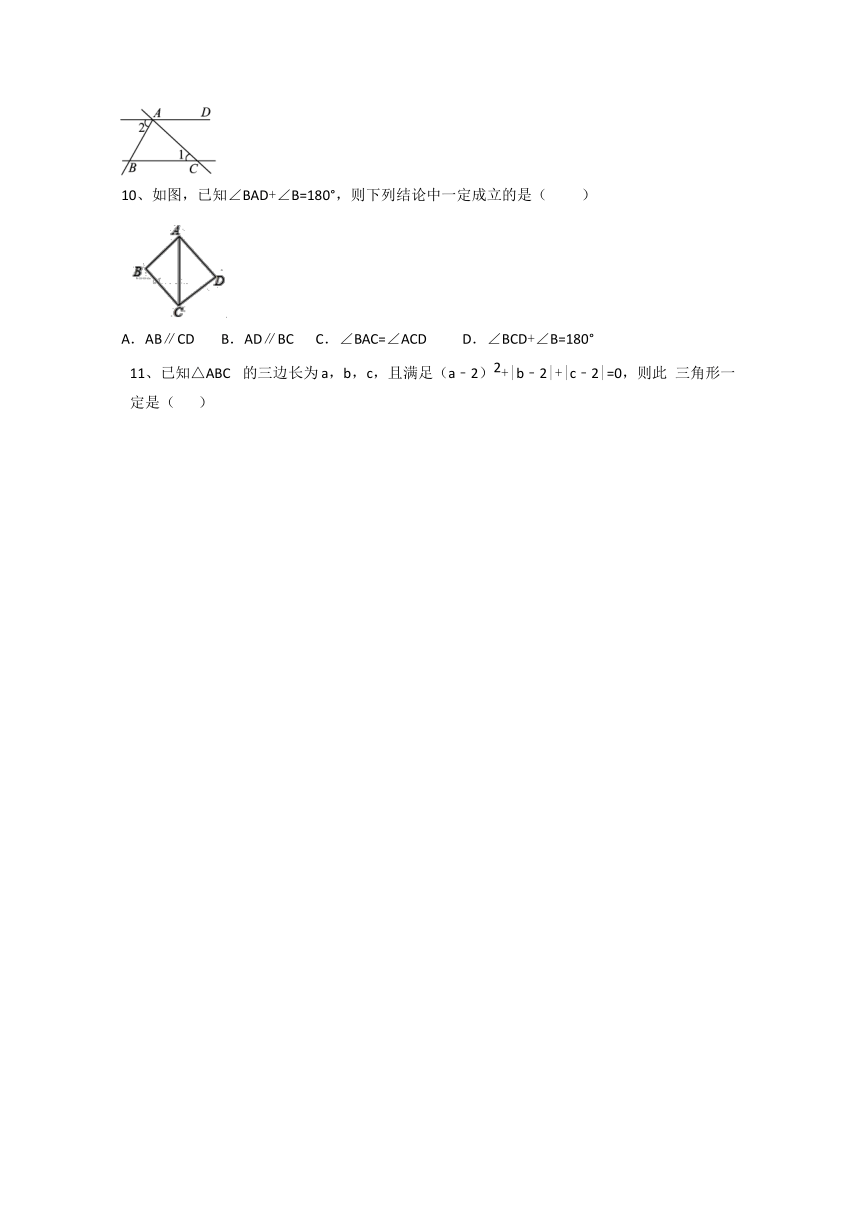
10、如图,已知∠BAD+∠B=180°,则下列结论中一定成立的是( )
A.AB∥CD B.AD∥BC C.∠BAC=∠ACD D.∠BCD+∠B=180°
11、已知△ABC 的三边长为 a,b,c,且满足(a﹣2)2+|b﹣2|+|c﹣2|=0,则此 三角形一定是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.一般三角形
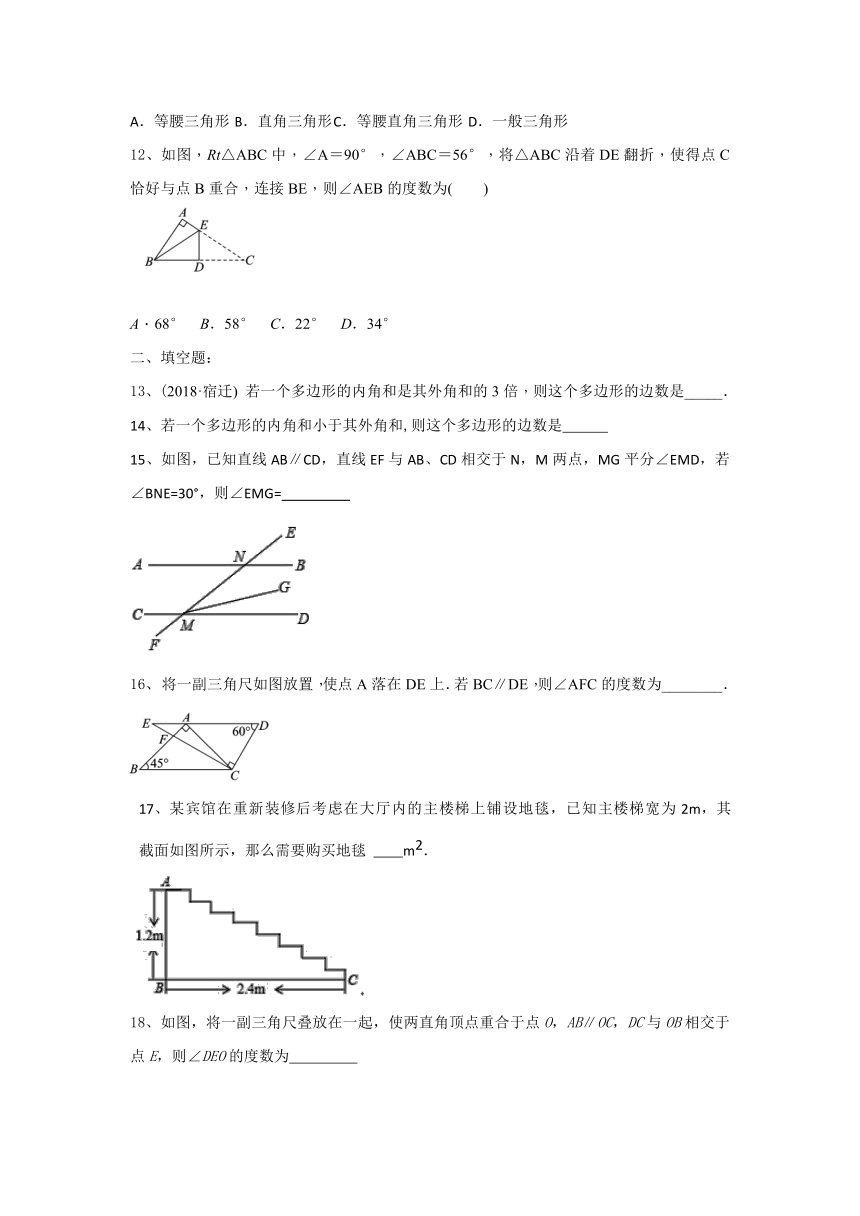
12、如图,Rt△ABC中,∠A=90°,∠ABC=56°,将△ABC沿着DE翻折,使得点C恰好与点B重合,连接BE,则∠AEB的度数为( )
A.68° B.58° C.22° D.34°
二、填空题:
13、(2018·宿迁) 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_____.
14、若一个多边形的内角和小于其外角和,则这个多边形的边数是
15、如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG=
16、 将一副三角尺如图放置,使点A落在DE上.若BC∥DE,则∠AFC的度数为________.
17、某宾馆在重新装修后考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽为2m,其截面如图所示,那么需要购买地毯 m2.
18、如图,将一副三角尺叠放在一起,使两直角顶点重合于点O,AB∥OC,DC与OB相交于点E,则∠DEO的度数为
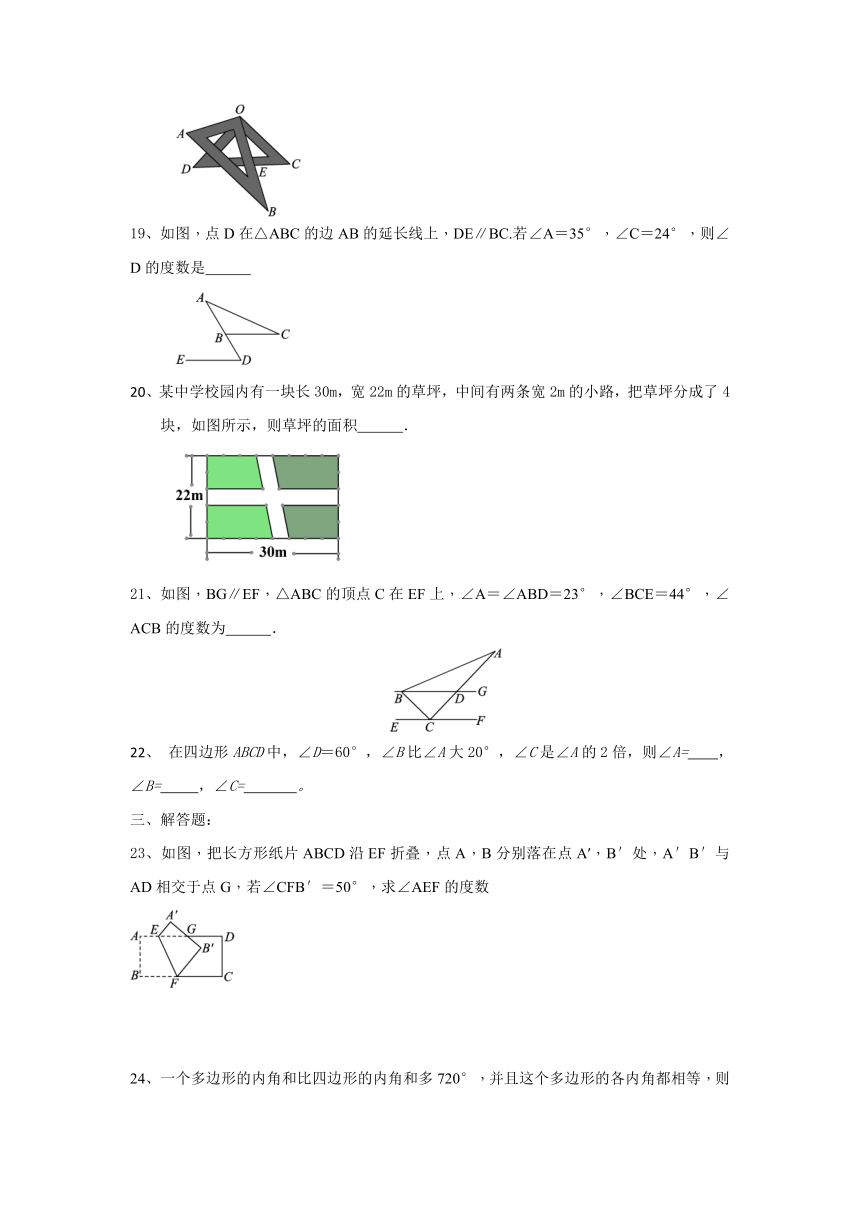
19、如图,点D在△ABC的边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是
20、某中学校园内有一块长30m,宽22m的草坪,中间有两条宽2m的小路,把草坪分成了4块,如图所示,则草坪的面积 .
21、如图,BG∥EF,△ABC的顶点C在EF上,∠A=∠ABD=23°,∠BCE=44°,∠ACB的度数为 .
22、 在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,则∠A= ,∠B= ,∠C= 。
三、解答题:
23、如图,把长方形纸片ABCD沿EF折叠,点A,B分别落在点A′,B′处,A′B′与AD相交于点G,若∠CFB′=50°,求∠AEF的度数
24、一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,则这个多边形的每个内角是多少度?
25、画图题:
(1)画出图中△ABC的高AD(标注出点D的位置);
(2)画出把△ABC沿射线AD方向平移2 cm后得到的△A1B1C1;
(3)根据“图形平移”的性质,得BB1=________cm,AC与A1C1的关系是________________.
26、如图,点D、E在BC上,∠BDF、∠AEG都是直角,且∠1=∠2.
(1)若∠2=3∠4,求∠1的度数.
(2)探究∠3与∠4的关系,并说明理由.
27、直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
一、选择题:
1、C
2、A
3、D
4、A
5、D
6、B
7、C
8、A
9、C
10、B
11、A
12、A
二、填空题:
13、8
14、3
15、15°
16、75°
17、7.2
18、75°
19、59°
20、660
21、90°
22、70° 90° 140°
三、解答题:
23、长方形ABCD沿EF折叠后,点A′,B′分别为点A,B的对应点,
∴∠BFE=∠EFB′.
∵∠CFB′=50°,∠BFE+∠EFB′+∠CFB′=180°,
∴∠BFE=65°.
∵AD∥BC,
∴∠AEF=180°-∠BFE=115°
24、设这个多边形的边数为n,
则(n-2)·180°=360°+720°,
解得n=8.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为1080°÷8=135°
25、(3)2 平行且相等
26、(1) 67.5° (2)等角的余角相等∴∠3=∠4
27、(1)解:∠AEB的大小不变, ∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE= ∠OAB/2,∠ABE= ∠ABO/2,
∴∠BAE+∠ABE= (∠OAB+∠ABO)/2=45°,
∴∠AEB=135°;
(2)解:∠CED的大小不变. 延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD= ∠BAP/2,∠ABC= ∠ABM/2,
∴∠BAD+∠ABC= (∠PAB+∠ABM)/2=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)解:(3)∵∠BAO与∠BOQ的角平分线相交于E, ∴∠EAO= ∠BAO/2,∠EOQ= ∠BOQ/2,
∴∠E=∠EOQ﹣∠EAO= (∠BOQ﹣∠BAO/2)= ∠ABO/2,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.?
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°.
∴∠ABO为60°或45°.
一、选择题:
1、(2018·南通)若一个凸多边形的内角和为720°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2、如图,AB∥DE,∠CDE=40°,则∠B的度数是( )
A.40° B.50° C.60° D.70°
3、如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
4、已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为( )
A.5 B.4 C.6 D.7
5、线段AB=5 cm,BC=2 cm,则A、C两点间的距离为 ( )
A.7 cm B.3 cm
C.7 cm或3 cm D.不小于3 cm且不大于7 cm
6、下列长度的三条线段,能组成三角形的是( )
A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cm
C.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm
7、如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D,E,F,则△ABC中BC边上的高是( )
A.CF B.BE C.AD D.CD
8、用一副三角板画角,不能画出的度数是( )
A.80° B.15° C.75° D.150°
9、如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( )
A.42° B.50° C.60° D.68°
10、如图,已知∠BAD+∠B=180°,则下列结论中一定成立的是( )
A.AB∥CD B.AD∥BC C.∠BAC=∠ACD D.∠BCD+∠B=180°
11、已知△ABC 的三边长为 a,b,c,且满足(a﹣2)2+|b﹣2|+|c﹣2|=0,则此 三角形一定是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.一般三角形
12、如图,Rt△ABC中,∠A=90°,∠ABC=56°,将△ABC沿着DE翻折,使得点C恰好与点B重合,连接BE,则∠AEB的度数为( )
A.68° B.58° C.22° D.34°
二、填空题:
13、(2018·宿迁) 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_____.
14、若一个多边形的内角和小于其外角和,则这个多边形的边数是
15、如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG=
16、 将一副三角尺如图放置,使点A落在DE上.若BC∥DE,则∠AFC的度数为________.
17、某宾馆在重新装修后考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽为2m,其截面如图所示,那么需要购买地毯 m2.
18、如图,将一副三角尺叠放在一起,使两直角顶点重合于点O,AB∥OC,DC与OB相交于点E,则∠DEO的度数为
19、如图,点D在△ABC的边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是
20、某中学校园内有一块长30m,宽22m的草坪,中间有两条宽2m的小路,把草坪分成了4块,如图所示,则草坪的面积 .
21、如图,BG∥EF,△ABC的顶点C在EF上,∠A=∠ABD=23°,∠BCE=44°,∠ACB的度数为 .
22、 在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,则∠A= ,∠B= ,∠C= 。
三、解答题:
23、如图,把长方形纸片ABCD沿EF折叠,点A,B分别落在点A′,B′处,A′B′与AD相交于点G,若∠CFB′=50°,求∠AEF的度数
24、一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,则这个多边形的每个内角是多少度?
25、画图题:
(1)画出图中△ABC的高AD(标注出点D的位置);
(2)画出把△ABC沿射线AD方向平移2 cm后得到的△A1B1C1;
(3)根据“图形平移”的性质,得BB1=________cm,AC与A1C1的关系是________________.
26、如图,点D、E在BC上,∠BDF、∠AEG都是直角,且∠1=∠2.
(1)若∠2=3∠4,求∠1的度数.
(2)探究∠3与∠4的关系,并说明理由.
27、直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
一、选择题:
1、C
2、A
3、D
4、A
5、D
6、B
7、C
8、A
9、C
10、B
11、A
12、A
二、填空题:
13、8
14、3
15、15°
16、75°
17、7.2
18、75°
19、59°
20、660
21、90°
22、70° 90° 140°
三、解答题:
23、长方形ABCD沿EF折叠后,点A′,B′分别为点A,B的对应点,
∴∠BFE=∠EFB′.
∵∠CFB′=50°,∠BFE+∠EFB′+∠CFB′=180°,
∴∠BFE=65°.
∵AD∥BC,
∴∠AEF=180°-∠BFE=115°
24、设这个多边形的边数为n,
则(n-2)·180°=360°+720°,
解得n=8.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为1080°÷8=135°
25、(3)2 平行且相等
26、(1) 67.5° (2)等角的余角相等∴∠3=∠4
27、(1)解:∠AEB的大小不变, ∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE= ∠OAB/2,∠ABE= ∠ABO/2,
∴∠BAE+∠ABE= (∠OAB+∠ABO)/2=45°,
∴∠AEB=135°;
(2)解:∠CED的大小不变. 延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD= ∠BAP/2,∠ABC= ∠ABM/2,
∴∠BAD+∠ABC= (∠PAB+∠ABM)/2=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)解:(3)∵∠BAO与∠BOQ的角平分线相交于E, ∴∠EAO= ∠BAO/2,∠EOQ= ∠BOQ/2,
∴∠E=∠EOQ﹣∠EAO= (∠BOQ﹣∠BAO/2)= ∠ABO/2,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.?
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°.
∴∠ABO为60°或45°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
