6.1 行星的运动 共33张PPT
文档属性
| 名称 | 6.1 行星的运动 共33张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-15 11:34:39 | ||
图片预览










文档简介
Law of Universal Gravitation
第六章万有引力定律
(一)知识与技能
1、知道地心说和日心说的基本内容。
2、知道开普勒行星运动定律,知道开普勒行星运动定律的科学价值,了解比值k与行星的质量无关,仅与太阳(中心天体)有关。
3、理解人们对行星运动的认识过程是漫长复杂的,真理是来之不易的。
(二)过程与方法
通过托勒密、哥白尼、第谷·布拉赫、开普勒等几位科学家对行星运动的不同认识,了解人类认识事物本质的曲折性,体会观察方法的巨大作用。
(三)情感、态度与价值观
1、体会科学家实事求是,不迷信权威,敢于探索的精神。
2、体会对描述自然追求简单和谐是科学研究的动力之一。
宇宙是什么
这是古老而永恒的话题
智慧的生命
对宇宙的思索永不停息
穿越时空去追寻历史的印迹
前人的思考
不断给我们智慧的启迪
6.1行星的运动
太阳系
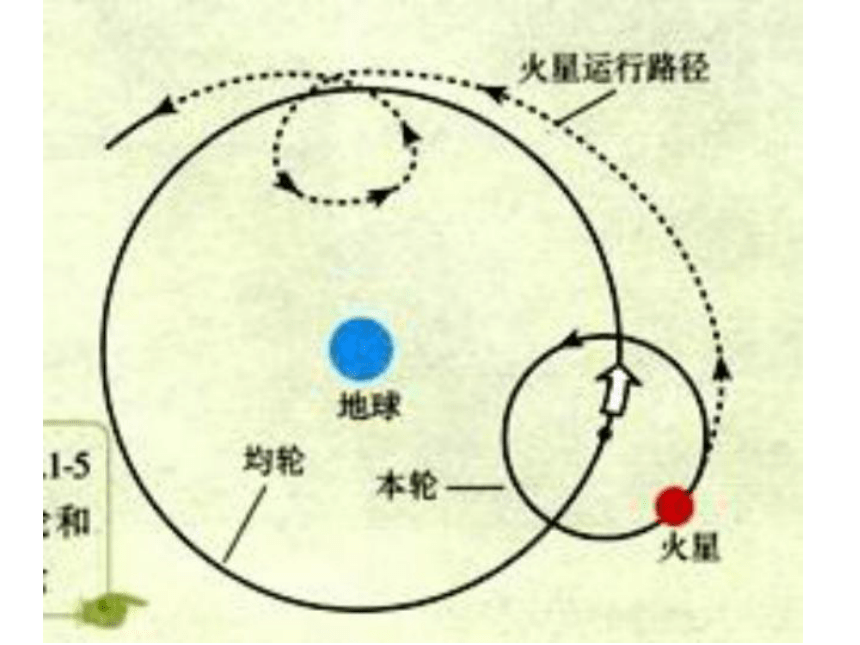
地球是世界的中心,并且静止不动,一切行星围绕地球做圆周运动
一、古人对天体运动认识的两种观点:
1、地心说
地心说是长期盛行于古代欧洲的宇宙学说。它最初由古希腊学者欧多克斯在公元前三世纪提出,后来经托勒密(90-168)进一步发展而逐渐建立和完善起来。
描述天体的运动遇到了困难
地心说直到16世纪才被哥白尼推翻.
*
BHJ
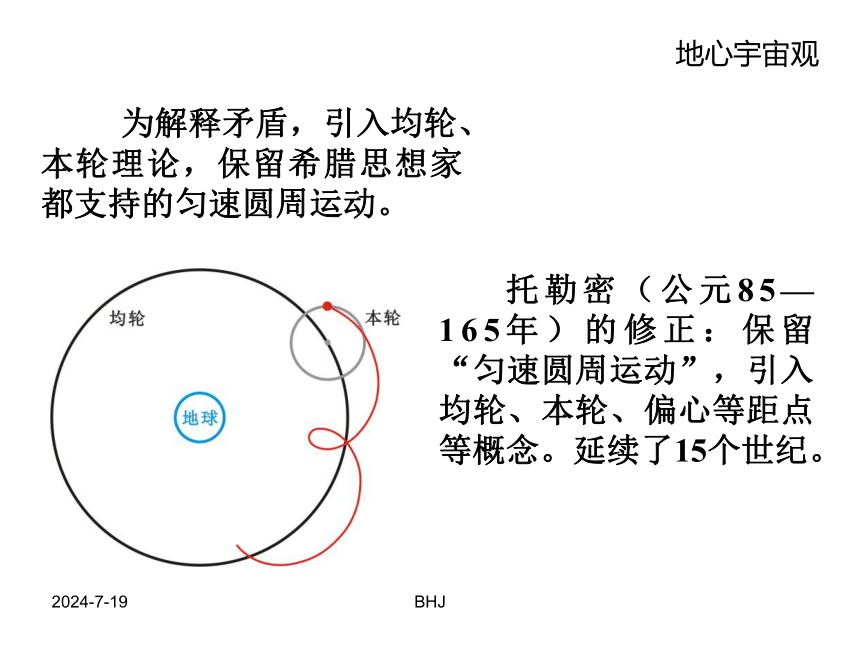
为解释矛盾,引入均轮、本轮理论,保留希腊思想家都支持的匀速圆周运动。
托勒密(公元85—165年)的修正:保留“匀速圆周运动”,引入均轮、本轮、偏心等距点等概念。延续了15个世纪。
地心宇宙观
太阳是世界的中心,并且静止不动,一切行星都围绕太阳做圆周运动。
2、日心说
随着天文观测不断进步,“地心说”暴露出许多问题。逐渐被波兰天文学家哥白尼(1473-1543)提出的“日心说”所取代。 波兰天文学家哥白尼经过近四十年的观测和计算,于1543年出版了“天体运行论”正式提出“日心说”。
“日心说”最终战胜了“地心说”并被古人们所接受
日心说触怒了教会,《天体运行论》列为禁书,布鲁诺殉难是哥白尼日心说经受的第一次考验 。
布鲁诺(Giordano Btuno,1548-1600) 意大利天文学家。
布鲁诺是日心说的宣传者和捍卫者。他还以天才的直觉发展了哥白尼的宇宙学说,提出了宇宙无限的思想。布鲁诺认为,宇宙是统一的、物质的、无限的,太阳系之外还有无数多个世界。布鲁诺超前于时代太多了,他的无限宇宙图景差不多300年后才得到科学界的公认。
日心宇宙观
布鲁诺的激进思想使天主教会暴跳如雷、恼羞成怒,1600年2月17日被宗教法庭处以火刑,活活烧死在罗马鲜花广场上。
意大利罗马鲜花广场
日心宇宙观
名人名言
黑暗即将过去,黎明即将到来,真理终将战胜邪恶!火,不能征服我,未来 的世界会了解我,会知道我的价值。
——布鲁诺临刑前的最后一句话
天才的观测家
多年精心观测得到大量的资料,为开普勒发现行星运动三定律奠定了基础
毕生精力投入到行星位置的测量中。在他以前,人们测量天体位置的误差大约是10′,第谷把这个不确定性减小到2′。他的观测结果为哥白尼的学说提供了关键性的支持。
(1546-1601)
第谷·布拉赫
日心说的进一步完善
德国天文学家开普勒(1571-1630)在最初研究他的导师家第谷(1546-1601)所记录的数据时,也是以行星绕太阳做匀速圆周运动的模型来思考问题的,但是所得结果却与第谷的观测数据至少有8分的角度误差。当时公认的第谷的观测误差不超过2分,开普勒想,这不容忽视的8分也许是因为人们认为行星绕太阳做匀速圆周运动所造成的。至此,人们长期以来视为真理的观念——天体做匀速圆周运动,第一次受到了怀疑。后来开普勒又仔细研究了第谷的观测资料,经过四年多的刻苦计算先后否定了19种设想,最后终于发现了天体运行的规律开普勒三大定律。
开普勒三定律
? 限于当时的科学发展水平,哥白尼的日心说 也有缺点和错误,这就是: (1)认为太阳是宇宙的中心,实际上,太阳只是太阳系中的一个中心天体,不是宇宙的中心,也并非静止,它在以2.46亿年的周期绕银河系中心 运动。 (2)沿用了行星在圆轨道作匀速圆周运动的旧观 念,实际上行星轨道是椭圆的,运动速度的大小也不是恒定的。
哥白尼日心说的局限
按照匀速圆周运动进行尝试性计算.
与第谷的观测数据有8 ′的角度偏差.
哥白尼的“完美”的匀速圆周
运动第一次受到了怀疑.
开普勒,数学天才,德国天文学 家,第谷的助手,擅长数学归纳
怎么回事……..
行星轨道是椭圆的
1609年,我将第一定律和第二定律发表于新出版的《新天文学》上
开普勒第一定律
开普勒第一定律:(椭圆轨道定律)所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
关于椭圆
开普勒第二定律:(面积定律)
对于任意一个行星来说,它与太阳的连线在相等的时间里扫过的面积相等。SAB=SCD=SEK
开普勒第二定律
若tAB= tCD = tEK ,则sAB= sCD = sEK
行星在近日点A处速度必最大,在远日点B处速度必最小
开普勒第二定律:(面积定律)
对于任意一个行星来说,它与太阳的连线在相等的时间里扫过的面积相等。SAB=SCD=SEK
开普勒第二定律
若tAB= tCD = tEK ,则sAB= sCD = sEK
θ
行星在相同时间?t内经过的区域如图中三角形的面积
其中θ为r、v正向夹角
行星在近日点A处速度必最大,在远日点B处速度必最小
思考:离太阳越远的行星其周期也越大吗?
a3/T2=k
注意: k的大小与行星无关,只与中心天体有关!
开普勒第三定律
开普勒第三定律:(周期定律)
所有行星的轨道的半长轴的立方和公转周期的平方成正比。
注意:1.K是一个常量,它与行星无关,与中心天体有关。
2.轨道半长轴越大,公转周期越大.
探究K值的决定因素:
K是一个只与中心天体质量有关的物理量
行星
或卫星 中心体 半长轴(x106km) 公转周期(天) K值
水星
太阳 57 87.97 3.36×1018
金星 108 225 3.35×1018
火星 228 687 3.36×1018
同步卫星 地球 0.0424 1 1.02×1013
月球 0.3844 27.322 1.02×1013
k=a3 /T2/(m3 ? s2)
结 论
你从中发现了什么?
行星 半长轴a/106 km 公转周期/T
水星 57 87.97
金星 108 225
地球 149 365
火星 228 687
木星 778 4333
土星 1426 10759
天王星 2869 30686
海王星 4495 60188
开普勒第一定律——轨道定律
所有行星都分别在大小不同的椭圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上;
开普勒第二定律——面积定律
对某个行星来说,太阳和行星的连线在相等的时间扫过相等的面积;
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
即有: a13:T12=a3:T2
注意: k的大小与行星无关,只与中心天体有关。
开普勒三定律
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心
1.所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上
2. 对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等
2.对于某一行星来说,它绕太阳做圆周运动的角速度(或线速度)不变,即行星做匀速圆周运动
3.所有行星的轨道半径的三次方跟公转周期的二次方的比值都相等
即r?/T?=k
在中学阶段,我们将椭圆轨道按照圆形轨道
处理,则开普勒定律描述为:
观察下图是按不同比例尺绘制的太阳系八颗行星及冥王星的轨道
实际上,行星的轨道与圆十分接近,所以在中学阶段的研究中我们按圆轨道处理.这样就可以说:
①行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
②对某一行星来说,它绕太阳做圆周运动的角速度(线速度)大小不变,即行星做匀速圆周运动。
③所有行星轨道半径的三次方跟它的公转周期的二次方的比值都相等。
例题1
神舟六号沿半径为R的圆周绕地球运动,其周期为T,如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的特殊椭圆轨道运动,椭圆和地球表面在B点相切,如图所示,如果地球半径为r,求飞船由A点到B点所需的时间。
例2.有两个人造地球卫星,它们绕地球运转的轨道半径之比是1:2,则它们绕地球运转的周期之比为 。
练习、月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天,有一颗人造卫星在赤道平面内绕地球转动,地面上的人感觉它就像停留在空中不动一样,求该卫星离地的高度 ?
(地球半径R地=6.4×103 km)
解:设人造地球卫星运行半径为R,周期为T,根据开普勒第三定律有:
由以上两式可得:
在赤道平面内离地面高度:
点评:随地球一起转动,就好像停留在天空中的卫星,通常称之为定点卫星.它们离地面的高度是一个确定的值,不能随意变动。
例题:月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地面多少高度,人造地球卫星可以随地球一起转动,就像停留在无空中不动一样. (R=6.4×106m )
第六章万有引力定律
(一)知识与技能
1、知道地心说和日心说的基本内容。
2、知道开普勒行星运动定律,知道开普勒行星运动定律的科学价值,了解比值k与行星的质量无关,仅与太阳(中心天体)有关。
3、理解人们对行星运动的认识过程是漫长复杂的,真理是来之不易的。
(二)过程与方法
通过托勒密、哥白尼、第谷·布拉赫、开普勒等几位科学家对行星运动的不同认识,了解人类认识事物本质的曲折性,体会观察方法的巨大作用。
(三)情感、态度与价值观
1、体会科学家实事求是,不迷信权威,敢于探索的精神。
2、体会对描述自然追求简单和谐是科学研究的动力之一。
宇宙是什么
这是古老而永恒的话题
智慧的生命
对宇宙的思索永不停息
穿越时空去追寻历史的印迹
前人的思考
不断给我们智慧的启迪
6.1行星的运动
太阳系
地球是世界的中心,并且静止不动,一切行星围绕地球做圆周运动
一、古人对天体运动认识的两种观点:
1、地心说
地心说是长期盛行于古代欧洲的宇宙学说。它最初由古希腊学者欧多克斯在公元前三世纪提出,后来经托勒密(90-168)进一步发展而逐渐建立和完善起来。
描述天体的运动遇到了困难
地心说直到16世纪才被哥白尼推翻.
*
BHJ
为解释矛盾,引入均轮、本轮理论,保留希腊思想家都支持的匀速圆周运动。
托勒密(公元85—165年)的修正:保留“匀速圆周运动”,引入均轮、本轮、偏心等距点等概念。延续了15个世纪。
地心宇宙观
太阳是世界的中心,并且静止不动,一切行星都围绕太阳做圆周运动。
2、日心说
随着天文观测不断进步,“地心说”暴露出许多问题。逐渐被波兰天文学家哥白尼(1473-1543)提出的“日心说”所取代。 波兰天文学家哥白尼经过近四十年的观测和计算,于1543年出版了“天体运行论”正式提出“日心说”。
“日心说”最终战胜了“地心说”并被古人们所接受
日心说触怒了教会,《天体运行论》列为禁书,布鲁诺殉难是哥白尼日心说经受的第一次考验 。
布鲁诺(Giordano Btuno,1548-1600) 意大利天文学家。
布鲁诺是日心说的宣传者和捍卫者。他还以天才的直觉发展了哥白尼的宇宙学说,提出了宇宙无限的思想。布鲁诺认为,宇宙是统一的、物质的、无限的,太阳系之外还有无数多个世界。布鲁诺超前于时代太多了,他的无限宇宙图景差不多300年后才得到科学界的公认。
日心宇宙观
布鲁诺的激进思想使天主教会暴跳如雷、恼羞成怒,1600年2月17日被宗教法庭处以火刑,活活烧死在罗马鲜花广场上。
意大利罗马鲜花广场
日心宇宙观
名人名言
黑暗即将过去,黎明即将到来,真理终将战胜邪恶!火,不能征服我,未来 的世界会了解我,会知道我的价值。
——布鲁诺临刑前的最后一句话
天才的观测家
多年精心观测得到大量的资料,为开普勒发现行星运动三定律奠定了基础
毕生精力投入到行星位置的测量中。在他以前,人们测量天体位置的误差大约是10′,第谷把这个不确定性减小到2′。他的观测结果为哥白尼的学说提供了关键性的支持。
(1546-1601)
第谷·布拉赫
日心说的进一步完善
德国天文学家开普勒(1571-1630)在最初研究他的导师家第谷(1546-1601)所记录的数据时,也是以行星绕太阳做匀速圆周运动的模型来思考问题的,但是所得结果却与第谷的观测数据至少有8分的角度误差。当时公认的第谷的观测误差不超过2分,开普勒想,这不容忽视的8分也许是因为人们认为行星绕太阳做匀速圆周运动所造成的。至此,人们长期以来视为真理的观念——天体做匀速圆周运动,第一次受到了怀疑。后来开普勒又仔细研究了第谷的观测资料,经过四年多的刻苦计算先后否定了19种设想,最后终于发现了天体运行的规律开普勒三大定律。
开普勒三定律
? 限于当时的科学发展水平,哥白尼的日心说 也有缺点和错误,这就是: (1)认为太阳是宇宙的中心,实际上,太阳只是太阳系中的一个中心天体,不是宇宙的中心,也并非静止,它在以2.46亿年的周期绕银河系中心 运动。 (2)沿用了行星在圆轨道作匀速圆周运动的旧观 念,实际上行星轨道是椭圆的,运动速度的大小也不是恒定的。
哥白尼日心说的局限
按照匀速圆周运动进行尝试性计算.
与第谷的观测数据有8 ′的角度偏差.
哥白尼的“完美”的匀速圆周
运动第一次受到了怀疑.
开普勒,数学天才,德国天文学 家,第谷的助手,擅长数学归纳
怎么回事……..
行星轨道是椭圆的
1609年,我将第一定律和第二定律发表于新出版的《新天文学》上
开普勒第一定律
开普勒第一定律:(椭圆轨道定律)所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
关于椭圆
开普勒第二定律:(面积定律)
对于任意一个行星来说,它与太阳的连线在相等的时间里扫过的面积相等。SAB=SCD=SEK
开普勒第二定律
若tAB= tCD = tEK ,则sAB= sCD = sEK
行星在近日点A处速度必最大,在远日点B处速度必最小
开普勒第二定律:(面积定律)
对于任意一个行星来说,它与太阳的连线在相等的时间里扫过的面积相等。SAB=SCD=SEK
开普勒第二定律
若tAB= tCD = tEK ,则sAB= sCD = sEK
θ
行星在相同时间?t内经过的区域如图中三角形的面积
其中θ为r、v正向夹角
行星在近日点A处速度必最大,在远日点B处速度必最小
思考:离太阳越远的行星其周期也越大吗?
a3/T2=k
注意: k的大小与行星无关,只与中心天体有关!
开普勒第三定律
开普勒第三定律:(周期定律)
所有行星的轨道的半长轴的立方和公转周期的平方成正比。
注意:1.K是一个常量,它与行星无关,与中心天体有关。
2.轨道半长轴越大,公转周期越大.
探究K值的决定因素:
K是一个只与中心天体质量有关的物理量
行星
或卫星 中心体 半长轴(x106km) 公转周期(天) K值
水星
太阳 57 87.97 3.36×1018
金星 108 225 3.35×1018
火星 228 687 3.36×1018
同步卫星 地球 0.0424 1 1.02×1013
月球 0.3844 27.322 1.02×1013
k=a3 /T2/(m3 ? s2)
结 论
你从中发现了什么?
行星 半长轴a/106 km 公转周期/T
水星 57 87.97
金星 108 225
地球 149 365
火星 228 687
木星 778 4333
土星 1426 10759
天王星 2869 30686
海王星 4495 60188
开普勒第一定律——轨道定律
所有行星都分别在大小不同的椭圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上;
开普勒第二定律——面积定律
对某个行星来说,太阳和行星的连线在相等的时间扫过相等的面积;
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
即有: a13:T12=a3:T2
注意: k的大小与行星无关,只与中心天体有关。
开普勒三定律
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心
1.所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上
2. 对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等
2.对于某一行星来说,它绕太阳做圆周运动的角速度(或线速度)不变,即行星做匀速圆周运动
3.所有行星的轨道半径的三次方跟公转周期的二次方的比值都相等
即r?/T?=k
在中学阶段,我们将椭圆轨道按照圆形轨道
处理,则开普勒定律描述为:
观察下图是按不同比例尺绘制的太阳系八颗行星及冥王星的轨道
实际上,行星的轨道与圆十分接近,所以在中学阶段的研究中我们按圆轨道处理.这样就可以说:
①行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
②对某一行星来说,它绕太阳做圆周运动的角速度(线速度)大小不变,即行星做匀速圆周运动。
③所有行星轨道半径的三次方跟它的公转周期的二次方的比值都相等。
例题1
神舟六号沿半径为R的圆周绕地球运动,其周期为T,如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的特殊椭圆轨道运动,椭圆和地球表面在B点相切,如图所示,如果地球半径为r,求飞船由A点到B点所需的时间。
例2.有两个人造地球卫星,它们绕地球运转的轨道半径之比是1:2,则它们绕地球运转的周期之比为 。
练习、月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天,有一颗人造卫星在赤道平面内绕地球转动,地面上的人感觉它就像停留在空中不动一样,求该卫星离地的高度 ?
(地球半径R地=6.4×103 km)
解:设人造地球卫星运行半径为R,周期为T,根据开普勒第三定律有:
由以上两式可得:
在赤道平面内离地面高度:
点评:随地球一起转动,就好像停留在天空中的卫星,通常称之为定点卫星.它们离地面的高度是一个确定的值,不能随意变动。
例题:月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地面多少高度,人造地球卫星可以随地球一起转动,就像停留在无空中不动一样. (R=6.4×106m )
