高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件 新人教B版选修2_1(30张)
文档属性
| 名称 | 高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件 新人教B版选修2_1(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-16 12:58:32 | ||
图片预览









文档简介
课件30张PPT。椭圆的标准方程 1.圆的定义:平面内与定点距离等于
定长的点的集合(轨迹)2.圆上的点满足的几何条件:这里定点为O ,定长为半径r.MO复习回顾2.求曲线方程的一般步骤: (1)建系
(2)设点
(3)列式
(4)化简
(5)证明复习回顾下面我们一起来
观看一些图片!思考1:我们如何来画椭圆呢?思考2:如果我们把一个定点改为
两个,定长改为动点到定
点的距离之和为常数的话,
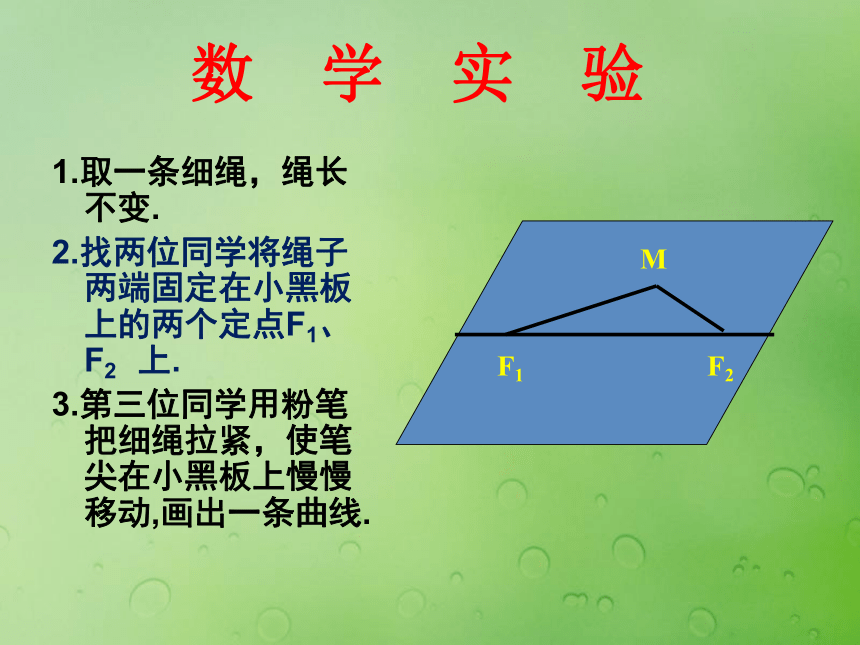
动点的轨迹是什么呢?下面我们来动手操作一下吧!数 学 实 验1.取一条细绳,绳长不变.
2.找两位同学将绳子两端固定在小黑板上的两个定点F1、F2 上.
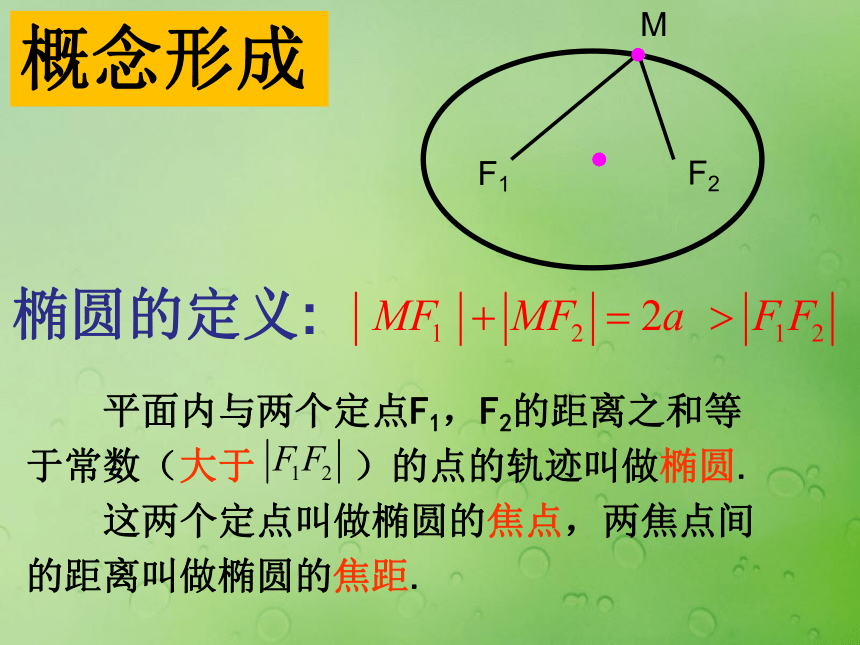
3.第三位同学用粉笔把细绳拉紧,使笔尖在小黑板上慢慢移动,画出一条曲线.概念形成 平面内与两个定点F1,F2的距离之和等于常数(大于 )的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.椭圆的定义:MF1 F2 动点M的轨迹:是线段F1F2 . F1 F2 动点M的轨迹:不存在. 概念辨析用定义判断下列动点M的轨迹是否为椭圆.(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹.是不是是 概念辨析椭圆方程的推导基本步骤:(1)建系
(2)设点
(3)列式(4)化简
(5)证明新知探究? 探讨建立平面直角坐标系的方案方案一原则:尽可能使方程的形式简单、运算简单
注意: 一般利用对称轴或已有的互相垂直的线段所
在的直线作为坐标轴.(对称、“简洁”)MF1 F2 新知探究x解:设M (x, y)是椭圆上任意一点,
椭圆的焦距|F1F2|=2c(c>0),
则F1、F2的坐标分别是(?c,0)、(c,0) .
P与F1和F2的距离的和为固定值2a(2a>2c) (问题:下面怎样化简呢?)由椭圆的定义得,限制条件:由于得方程椭圆方程的推导椭圆的 标准方程:椭圆的标准方程椭圆的标准方程形成结论新知探究定 义图 形方 程焦点坐标F(±c,0)F(0,±c)a,b,c之间的关系|MF1|+|MF2|=2a (2a>2c>0)椭圆的标准方程求法:一定焦点位置;二设椭圆方程;三求a、b的值.焦点位置的判断分母哪个大,焦点就在哪个轴上.则a= ,b= ;则a= ,b= ;5346快速抢答:则a= ,b= ;则a= ,b= .3典例讲解例1. 根据条件求椭圆的标准方程:
(1)解:
(2)解:⑴⑵例2:课堂小结:椭圆一个概念:二个方程:三个意识:求美意识, 求简意识,前瞻意识三个思想:①整体思想②数形结合思想③方程思想当堂检测答案D 2. D3.4. 11或295.解析:由已知1.教材42-43页:练习A和练习B.
2.练习册对应习题.课后作业: 谢谢,再见!
定长的点的集合(轨迹)2.圆上的点满足的几何条件:这里定点为O ,定长为半径r.MO复习回顾2.求曲线方程的一般步骤: (1)建系
(2)设点
(3)列式
(4)化简
(5)证明复习回顾下面我们一起来
观看一些图片!思考1:我们如何来画椭圆呢?思考2:如果我们把一个定点改为
两个,定长改为动点到定
点的距离之和为常数的话,
动点的轨迹是什么呢?下面我们来动手操作一下吧!数 学 实 验1.取一条细绳,绳长不变.
2.找两位同学将绳子两端固定在小黑板上的两个定点F1、F2 上.
3.第三位同学用粉笔把细绳拉紧,使笔尖在小黑板上慢慢移动,画出一条曲线.概念形成 平面内与两个定点F1,F2的距离之和等于常数(大于 )的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.椭圆的定义:MF1 F2 动点M的轨迹:是线段F1F2 . F1 F2 动点M的轨迹:不存在. 概念辨析用定义判断下列动点M的轨迹是否为椭圆.(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹.是不是是 概念辨析椭圆方程的推导基本步骤:(1)建系
(2)设点
(3)列式(4)化简
(5)证明新知探究? 探讨建立平面直角坐标系的方案方案一原则:尽可能使方程的形式简单、运算简单
注意: 一般利用对称轴或已有的互相垂直的线段所
在的直线作为坐标轴.(对称、“简洁”)MF1 F2 新知探究x解:设M (x, y)是椭圆上任意一点,
椭圆的焦距|F1F2|=2c(c>0),
则F1、F2的坐标分别是(?c,0)、(c,0) .
P与F1和F2的距离的和为固定值2a(2a>2c) (问题:下面怎样化简呢?)由椭圆的定义得,限制条件:由于得方程椭圆方程的推导椭圆的 标准方程:椭圆的标准方程椭圆的标准方程形成结论新知探究定 义图 形方 程焦点坐标F(±c,0)F(0,±c)a,b,c之间的关系|MF1|+|MF2|=2a (2a>2c>0)椭圆的标准方程求法:一定焦点位置;二设椭圆方程;三求a、b的值.焦点位置的判断分母哪个大,焦点就在哪个轴上.则a= ,b= ;则a= ,b= ;5346快速抢答:则a= ,b= ;则a= ,b= .3典例讲解例1. 根据条件求椭圆的标准方程:
(1)解:
(2)解:⑴⑵例2:课堂小结:椭圆一个概念:二个方程:三个意识:求美意识, 求简意识,前瞻意识三个思想:①整体思想②数形结合思想③方程思想当堂检测答案D 2. D3.4. 11或295.解析:由已知1.教材42-43页:练习A和练习B.
2.练习册对应习题.课后作业: 谢谢,再见!
