八年级数学上册第十四章勾股定理14.2勾股定理的应用 作业新版华东师大版
文档属性
| 名称 | 八年级数学上册第十四章勾股定理14.2勾股定理的应用 作业新版华东师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 51.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-16 13:42:46 | ||
图片预览

文档简介
14.2勾股定理的应用(1)
1.小丰的妈妈买了一部29英寸(74cm)的电视机,下列对29英寸的说法中正确的是( )
A.
小丰认为指的是屏幕的长度
B.
小丰的妈妈认为指的是屏幕的宽度
C.
小丰的爸爸认为指的是屏幕的周长
D.
售货员认为指的是屏幕对角线的长度
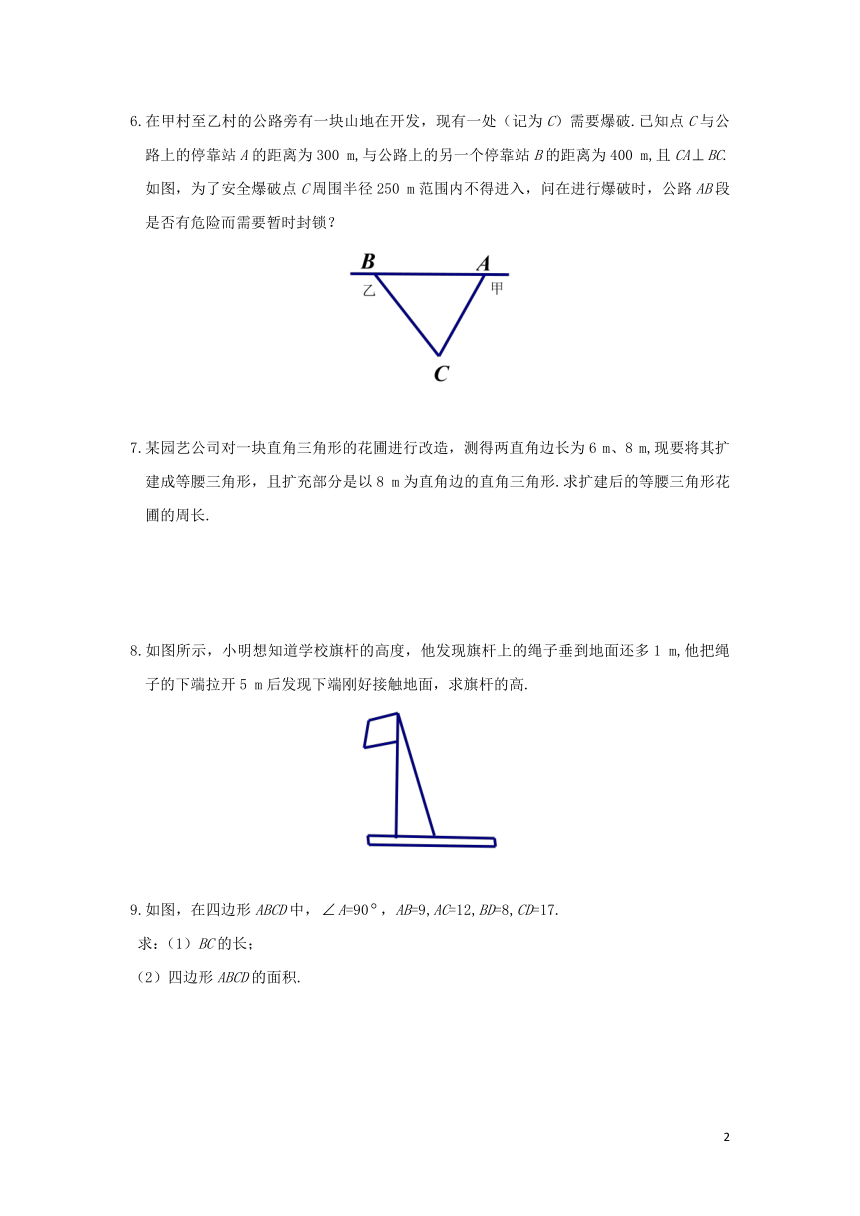
2.由于台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树在折断前(不包括树根)长度是( )
A.
8m
B.
10m
C.
16m
D.
18m
3.如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A点相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
A.
()cm
B.
C.
D.
9cm
4.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )
A.
12米
B.
13米
C.
14米
D.
15米
5.如图某中学有一块三角形的花圃ABC,现在测量得A=45,BC=5m,AC边上的高为4 m,请你求出这块花圃的面积.
6.在甲村至乙村的公路旁有一块山地在开发,现有一处(记为C)需要爆破.已知点C与公路上的停靠站A的距离为300 m,与公路上的另一个停靠站B的距离为400 m,且CABC.如图,为了安全爆破点C周围半径250 m范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?
7.某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6 m、8 m,现要将其扩建成等腰三角形,且扩充部分是以8 m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.
8.如图所示,小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1 m,他把绳子的下端拉开5 m后发现下端刚好接触地面,求旗杆的高.
9.如图,在四边形ABCD中,A=90,AB=9,AC=12,BD=8,CD=17.
求:(1)BC的长;
(2)四边形ABCD的面积.
10.如图所示,南北向PQ为我国的领海线,PQ以东为我国领海,以西为公海.晚上10点23分,我国边防巡逻艇122号在A处发现其正西方面有一可疑船只C向A处靠近,便立即通知正在PQ上B处巡逻的123号艇注意其动向.经观测发现A与可疑船只之间的距离为6海里,B艇与可疑船只之间的距离为8海里,若该可疑船只的速度为12.8海里/时,则该可疑船只最早在何时进入我国领海?
参考答案:
1.D
2.C
3.C
4.A
5.14m2
6.解:如图,过点C作CDAB于D.
BC=400 m,AC=300 m, ACB=90,
AB==500(m).
又=ABCD=ACBC,
500CD=300400,
CD=240(m).
又240m<250m.
有危险而需要暂时封锁.
7.解:如图,原来的花圃为RtABC,
其中BC=6 m,AC=8 m,ACB=90,
扩充后的花圃为RtACD, ACD=90,AC=CD=8 m,
所以AD= m,
故扩建后的等腰三角形花圃的周长=8+8+8 =(16+8 )(m).
8.12
9.(1)15(2)114
10.解:设PQ与AC相交于点D,则CDB=90,
∵AB=6,BC=8,AC=10,且,
∴ABC为直角三角形, ABC=90,
又∵BDAC,
∴该船进入我国领海最短距离为CD的长度.
又ABBC=ACBD,
∴BD==4.8(海里)
又∵BC=8, BD=4.8,
∴,
∴CD=6.4海里,
∴从C到D所需时间为6.412.8=0.5(小时)=30(分)
∴该可疑船只最早在晚上10点58分进入我国领海.
1.小丰的妈妈买了一部29英寸(74cm)的电视机,下列对29英寸的说法中正确的是( )
A.
小丰认为指的是屏幕的长度
B.
小丰的妈妈认为指的是屏幕的宽度
C.
小丰的爸爸认为指的是屏幕的周长
D.
售货员认为指的是屏幕对角线的长度
2.由于台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树在折断前(不包括树根)长度是( )
A.
8m
B.
10m
C.
16m
D.
18m
3.如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A点相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
A.
()cm
B.
C.
D.
9cm
4.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )
A.
12米
B.
13米
C.
14米
D.
15米
5.如图某中学有一块三角形的花圃ABC,现在测量得A=45,BC=5m,AC边上的高为4 m,请你求出这块花圃的面积.
6.在甲村至乙村的公路旁有一块山地在开发,现有一处(记为C)需要爆破.已知点C与公路上的停靠站A的距离为300 m,与公路上的另一个停靠站B的距离为400 m,且CABC.如图,为了安全爆破点C周围半径250 m范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?
7.某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6 m、8 m,现要将其扩建成等腰三角形,且扩充部分是以8 m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.
8.如图所示,小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1 m,他把绳子的下端拉开5 m后发现下端刚好接触地面,求旗杆的高.
9.如图,在四边形ABCD中,A=90,AB=9,AC=12,BD=8,CD=17.
求:(1)BC的长;
(2)四边形ABCD的面积.
10.如图所示,南北向PQ为我国的领海线,PQ以东为我国领海,以西为公海.晚上10点23分,我国边防巡逻艇122号在A处发现其正西方面有一可疑船只C向A处靠近,便立即通知正在PQ上B处巡逻的123号艇注意其动向.经观测发现A与可疑船只之间的距离为6海里,B艇与可疑船只之间的距离为8海里,若该可疑船只的速度为12.8海里/时,则该可疑船只最早在何时进入我国领海?
参考答案:
1.D
2.C
3.C
4.A
5.14m2
6.解:如图,过点C作CDAB于D.
BC=400 m,AC=300 m, ACB=90,
AB==500(m).
又=ABCD=ACBC,
500CD=300400,
CD=240(m).
又240m<250m.
有危险而需要暂时封锁.
7.解:如图,原来的花圃为RtABC,
其中BC=6 m,AC=8 m,ACB=90,
扩充后的花圃为RtACD, ACD=90,AC=CD=8 m,
所以AD= m,
故扩建后的等腰三角形花圃的周长=8+8+8 =(16+8 )(m).
8.12
9.(1)15(2)114
10.解:设PQ与AC相交于点D,则CDB=90,
∵AB=6,BC=8,AC=10,且,
∴ABC为直角三角形, ABC=90,
又∵BDAC,
∴该船进入我国领海最短距离为CD的长度.
又ABBC=ACBD,
∴BD==4.8(海里)
又∵BC=8, BD=4.8,
∴,
∴CD=6.4海里,
∴从C到D所需时间为6.412.8=0.5(小时)=30(分)
∴该可疑船只最早在晚上10点58分进入我国领海.
