高中数学第1章常用逻辑用语1.1.1四种命题课件 苏教版选修2_1(25张PPT)
文档属性
| 名称 | 高中数学第1章常用逻辑用语1.1.1四种命题课件 苏教版选修2_1(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 190.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-18 08:02:58 | ||
图片预览






文档简介
课件25张PPT。四种命题生活情景 假期里,妈妈要孩子做作业.
孩子:“如果你给我玩手机,那么我就做作业.”
妈妈:“如果你做作业,那么我就给你玩手机.”
孩子有点倔:“如果你不给我玩手机,那么我就不 做作业!”
妈妈火了:“如果你不做作业,那么我就不给你玩手机!”
一场冷战开始了…
请同学们分析一下这四句话结构上有什么特征?问题1 什么样的语句是命题?命题的一般形式是怎样的?
下面哪些语句是命题,如果是的话真假性如何?
①老师长得漂亮吗?
②同学们今天很高兴!
③同位角相等,两直线平行;
④若 ,则 ;命题:
能够判断真假的语句 其中判断为真的语句称为真命题,判断为假的语句称为假命题.问题2:
下面的语句的表述形式有什么特点? (1)若xy=1,则x、y互为倒数 ; (2)若A∪B=B,则 B A;
(3)同位角相等,两直线平行. 具有:“如果(若)…,那么(则)…”形式可以简记为“若P,则q”的形式命题中的P叫做命题的条件,q叫做命题的结论.问题3 (1)、结合本课一开始的生活情境,你还能用第③题中的命题构成更多的命题吗?
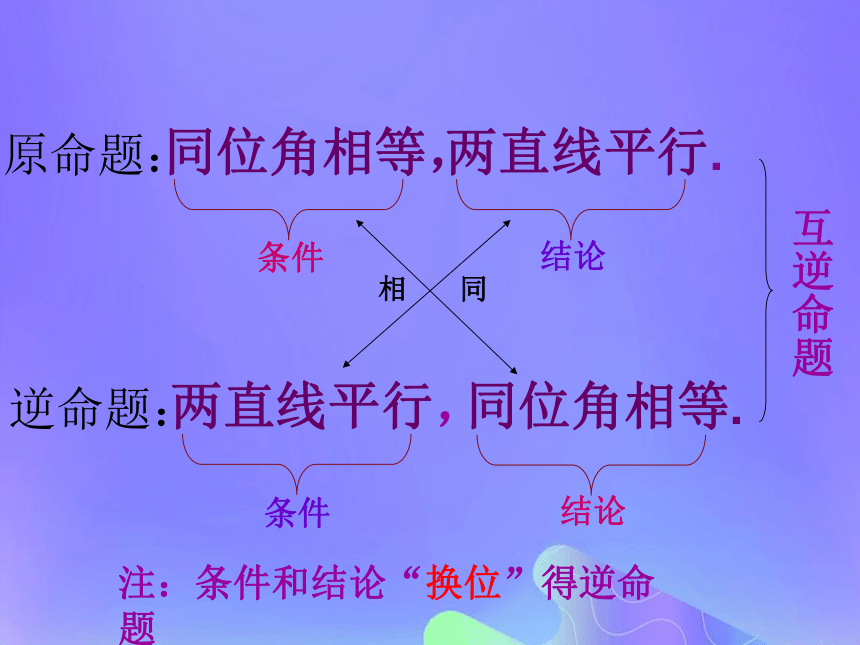
(2)你是否可以给新构成的命题命名呢? 同位角相等,同位角相等.两直线平行.
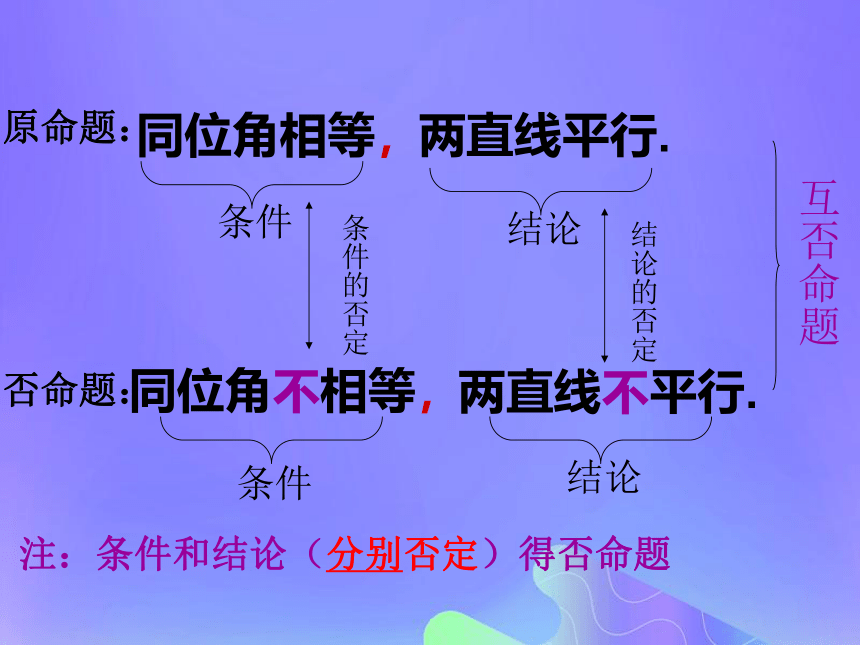
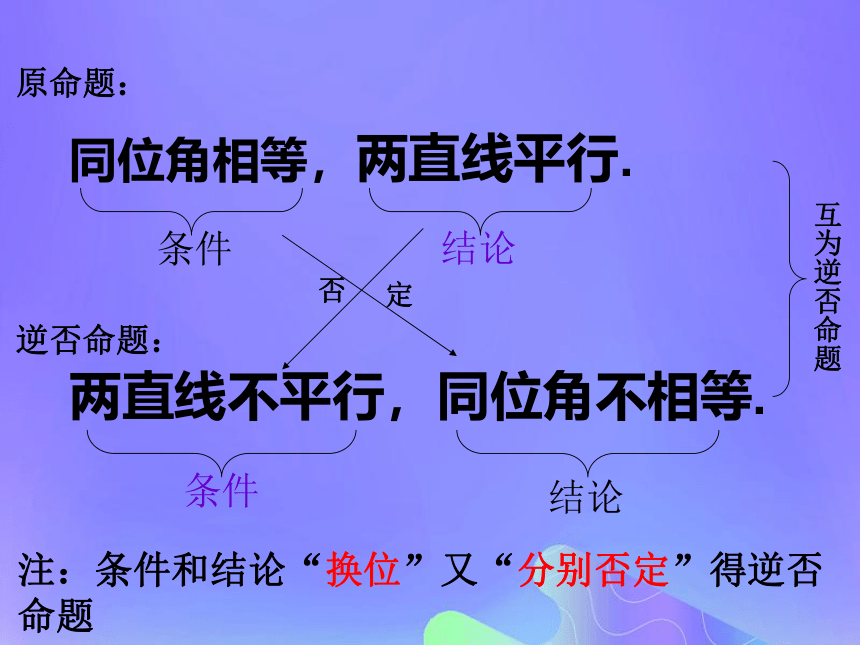
两直线平行,条件结论条件结论相同原命题:逆命题:互逆命题注:条件和结论“换位”得逆命题同位角相等,两直线平行.条件结论同位角不相等,两直线不平行.条件 结论条件的否定结论的否定互否命题原命题:否命题:注:条件和结论(分别否定)得否命题同位角相等,两直线平行.两直线不平行,同位角不相等.条件结论结论条件否定 互为逆否命题原命题:逆否命题:注:条件和结论“换位”又“分别否定”得逆否命题1 同位角相等,两直线平行.2 两直线平行,同位角相等.3 同位角不相等,两直线不平行.4 两直线不平行,同位角不相等.原命题:逆命题:否命题:逆否命题: 1 同位角相等,两直线平行.2 两直线平行,同位角相等.3同位角不相等,两直线不平行.4 两直线不平行,同位角不相等.逆命题: 原命题:逆否命题:否命题:练一练1 同位角相等,两直线平行.2 两直线平行,同位角相等.3 同位角不相等,两直线不平行.4 两直线不平行,同位角不相等.逆否命题:否命题:逆命题:原命题:练一练请思考:我们研究了命题①与另外三个命题的结构关系,考虑它们之间还有什么其它的结构关系吗?原命题
若p则q逆命题
若q则p否命题
若非p则非q逆否命题
若非q则非p互为否命题互为逆命题互为逆命题互为否命题互为逆否命题互为逆否命题若命题s是命题r的逆否命题,命题t是命题r的否命题,则命题s是t的 命题.逆命题r
若p则q命题t
若非 p则非 q命题s
若非 q则非p互逆 互否 互为逆否 解:原命题:若 ,则 成等比数列 逆命题:若 成等比数列 ,则 例1.写出命题“若 , 则 成等比数列”的逆命题、否命题、逆否命题,并判断各命题的真假. 逆否命题:若 不是等比数列,则 否命题:若 ,则 不是等比数列 (真)(真)(假)(假)例2.把下列命题改写成“若P则q”的形式,并写出它们的逆命题、否命题与逆否命题: 矩形的对角线相等。
矩形的对角线相等.解:原命题可以写成:若一个四边形是矩形,则它的对角线相等.逆命题:若一个四边形的对角线相等,则它是矩形.逆否命题:若一个四边形的对角线不相等,则它不是矩形. 否命题:若一个四边形不是矩形,则它的对角线不相等.(真)(真)(假)(假)写出下列命题的逆命题,并判断它们的真假:
(1)若X<Y,则Y>X (真)
(2)若a=0,则ab=0 (真)(1)逆命题:若Y>X,则X<Y真命题(2)逆命题:若ab=0,则a=0假命题原命题为真,逆命题不一定为真写出下列命题的否命题,并判断它们的真假:
(1)若X<Y,则Y>X (真)
(2)若a=0,则ab=0 (真)(1)否命题:若X≥Y,则Y≤X真命题(2)否命题:若a≠0,则ab≠0假命题原命题为真,否命题不一定为真写出下列命题的逆否命题,并判断它们的真假:
(1)若X<Y,则Y>X (真)
(2)若a=0,则ab=0 (真)(1)逆否命题:若Y≤X,则X≥Y真命题(2)逆否命题:若ab≠0,则a≠0真命题原命题为真,逆否命题为真. 下列说法中正确的有 __________
(1)四种命题中真命题的个数一定是偶数;
(2) 若一个命题的逆命题是真命题,则它的否命题不一定是真命题;
(3) 一个命题的逆命题与否命题之间是互为逆否关系;
(4) 若一个命题的逆否命题是假命题,则它的逆命题与否命题都是假命题.(1)考一考(3)2.判断命题:“若x2≠1,则x≠1”的真假.考一考解法一:可以直接判断该命题为真命题.解法二:命题:“若x2≠1,则x≠1”的逆否命题为:“若x=1,则x2=1”显然它为真命题.根据“互为逆否的两个命题同真同假”可知:命题:“若x2≠1,则x≠1”也为真命题.本节课你有什么收获?四种命题的关系. 四种命题的真假情况原命题
若p则q逆命题
若q则p否命题
若非 p则非 q逆否命题
若非 q则非p互为逆否 同真同假互为逆否 同真同假互否 真假无关互否 真假无关四种命题真假性之间的相互关系
孩子:“如果你给我玩手机,那么我就做作业.”
妈妈:“如果你做作业,那么我就给你玩手机.”
孩子有点倔:“如果你不给我玩手机,那么我就不 做作业!”
妈妈火了:“如果你不做作业,那么我就不给你玩手机!”
一场冷战开始了…
请同学们分析一下这四句话结构上有什么特征?问题1 什么样的语句是命题?命题的一般形式是怎样的?
下面哪些语句是命题,如果是的话真假性如何?
①老师长得漂亮吗?
②同学们今天很高兴!
③同位角相等,两直线平行;
④若 ,则 ;命题:
能够判断真假的语句 其中判断为真的语句称为真命题,判断为假的语句称为假命题.问题2:
下面的语句的表述形式有什么特点? (1)若xy=1,则x、y互为倒数 ; (2)若A∪B=B,则 B A;
(3)同位角相等,两直线平行. 具有:“如果(若)…,那么(则)…”形式可以简记为“若P,则q”的形式命题中的P叫做命题的条件,q叫做命题的结论.问题3 (1)、结合本课一开始的生活情境,你还能用第③题中的命题构成更多的命题吗?
(2)你是否可以给新构成的命题命名呢? 同位角相等,同位角相等.两直线平行.
两直线平行,条件结论条件结论相同原命题:逆命题:互逆命题注:条件和结论“换位”得逆命题同位角相等,两直线平行.条件结论同位角不相等,两直线不平行.条件 结论条件的否定结论的否定互否命题原命题:否命题:注:条件和结论(分别否定)得否命题同位角相等,两直线平行.两直线不平行,同位角不相等.条件结论结论条件否定 互为逆否命题原命题:逆否命题:注:条件和结论“换位”又“分别否定”得逆否命题1 同位角相等,两直线平行.2 两直线平行,同位角相等.3 同位角不相等,两直线不平行.4 两直线不平行,同位角不相等.原命题:逆命题:否命题:逆否命题: 1 同位角相等,两直线平行.2 两直线平行,同位角相等.3同位角不相等,两直线不平行.4 两直线不平行,同位角不相等.逆命题: 原命题:逆否命题:否命题:练一练1 同位角相等,两直线平行.2 两直线平行,同位角相等.3 同位角不相等,两直线不平行.4 两直线不平行,同位角不相等.逆否命题:否命题:逆命题:原命题:练一练请思考:我们研究了命题①与另外三个命题的结构关系,考虑它们之间还有什么其它的结构关系吗?原命题
若p则q逆命题
若q则p否命题
若非p则非q逆否命题
若非q则非p互为否命题互为逆命题互为逆命题互为否命题互为逆否命题互为逆否命题若命题s是命题r的逆否命题,命题t是命题r的否命题,则命题s是t的 命题.逆命题r
若p则q命题t
若非 p则非 q命题s
若非 q则非p互逆 互否 互为逆否 解:原命题:若 ,则 成等比数列 逆命题:若 成等比数列 ,则 例1.写出命题“若 , 则 成等比数列”的逆命题、否命题、逆否命题,并判断各命题的真假. 逆否命题:若 不是等比数列,则 否命题:若 ,则 不是等比数列 (真)(真)(假)(假)例2.把下列命题改写成“若P则q”的形式,并写出它们的逆命题、否命题与逆否命题: 矩形的对角线相等。
矩形的对角线相等.解:原命题可以写成:若一个四边形是矩形,则它的对角线相等.逆命题:若一个四边形的对角线相等,则它是矩形.逆否命题:若一个四边形的对角线不相等,则它不是矩形. 否命题:若一个四边形不是矩形,则它的对角线不相等.(真)(真)(假)(假)写出下列命题的逆命题,并判断它们的真假:
(1)若X<Y,则Y>X (真)
(2)若a=0,则ab=0 (真)(1)逆命题:若Y>X,则X<Y真命题(2)逆命题:若ab=0,则a=0假命题原命题为真,逆命题不一定为真写出下列命题的否命题,并判断它们的真假:
(1)若X<Y,则Y>X (真)
(2)若a=0,则ab=0 (真)(1)否命题:若X≥Y,则Y≤X真命题(2)否命题:若a≠0,则ab≠0假命题原命题为真,否命题不一定为真写出下列命题的逆否命题,并判断它们的真假:
(1)若X<Y,则Y>X (真)
(2)若a=0,则ab=0 (真)(1)逆否命题:若Y≤X,则X≥Y真命题(2)逆否命题:若ab≠0,则a≠0真命题原命题为真,逆否命题为真. 下列说法中正确的有 __________
(1)四种命题中真命题的个数一定是偶数;
(2) 若一个命题的逆命题是真命题,则它的否命题不一定是真命题;
(3) 一个命题的逆命题与否命题之间是互为逆否关系;
(4) 若一个命题的逆否命题是假命题,则它的逆命题与否命题都是假命题.(1)考一考(3)2.判断命题:“若x2≠1,则x≠1”的真假.考一考解法一:可以直接判断该命题为真命题.解法二:命题:“若x2≠1,则x≠1”的逆否命题为:“若x=1,则x2=1”显然它为真命题.根据“互为逆否的两个命题同真同假”可知:命题:“若x2≠1,则x≠1”也为真命题.本节课你有什么收获?四种命题的关系. 四种命题的真假情况原命题
若p则q逆命题
若q则p否命题
若非 p则非 q逆否命题
若非 q则非p互为逆否 同真同假互为逆否 同真同假互否 真假无关互否 真假无关四种命题真假性之间的相互关系
