一 平面直角坐标系 课件(32张PPT)
文档属性
| 名称 | 一 平面直角坐标系 课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 898.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-18 16:47:55 | ||
图片预览











文档简介
平面直角坐标系
1.体会直角坐标系的作用,掌握平面直角坐标系中刻画点的位置的方法和坐标法的解题步骤.
2.会运用坐标法解决实际问题与几何问题.
3.通过具体例子,了解在平面直角坐标系伸缩变换作用下平面图形的变化情况及作用.
1.数轴
它使直线上任一点P都可以由唯一的实数x确定.
2.平面直角坐标系
在平面上,当取定两条互相垂直的直线的交点为原点,并确定度量单位和这两条直线的方向,就建立了平面直角坐标系.它使平面上任一点P都可以由唯一的实数对(x,y)确定.
练习
3.定义
设P(x,y)是平面直角坐标系中任意一点,在变换
的作用下,点P(x,y)对应P′(x′,y′) 称为平面直角坐标系中的伸缩变换.
练习
B
到直角坐标系两坐标轴距离相等的点的轨迹方程是____________.
答案:y=x或y=-x
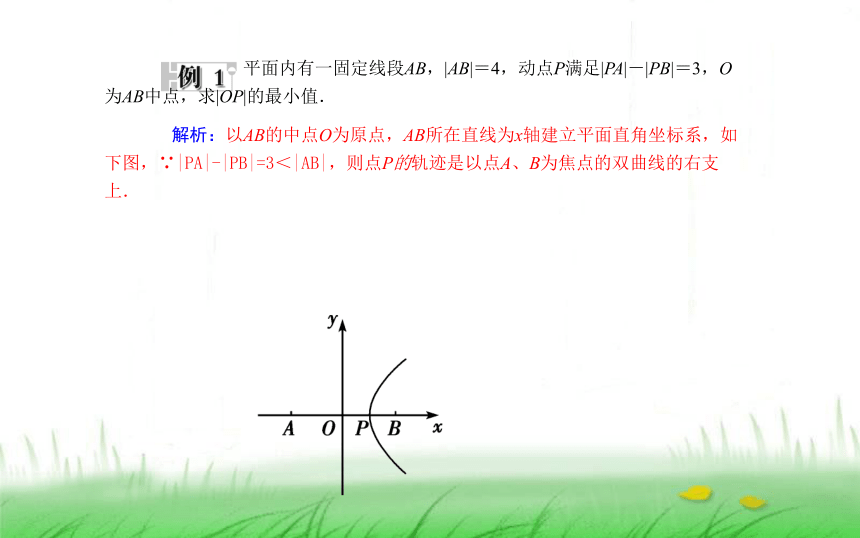
平面内有一固定线段AB,|AB|=4,动点P满足|PA|-|PB|=3,O为AB中点,求|OP|的最小值.
解析:以AB的中点O为原点,AB所在直线为x轴建立平面直角坐标系,如下图,∵|PA|-|PB|=3<|AB|,则点P的轨迹是以点A、B为焦点的双曲线的右支上.
由题意知2c=4,∴c=2.
把方程y=sin x变为y′= sin 4x′的伸缩变换公式为________.
把圆X2+Y2=16沿x轴方向均匀压缩为椭圆x2+ =1,则坐标变换公式是________.
分析:利用平面直角坐标系中的坐标伸缩变换公式求解.
1.在?ABCD中三个顶点A、B、C的坐标分别是(-1,2)、(3,0)、(5,1),则点D的坐标是( )
A.(9,-1) B.(-3,1)
C.(1,3) D.(2,2)
C
B
A
4.两个定点距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹 .
答案:x2+y2=4
5.在△ABC中,B(-2,0),C(2,0),△ABC的周长为10,求点A的轨迹方程为________.
6.已知圆的半径为6,圆内一定点P离圆心的距离为4,A,B是圆上的两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.
解析:如右图所示,以圆心O为原点,OP所在直线为x轴建立直角坐标系,则圆的方程为x2+y2=36,P(4,0).
7.求函数g(x)=| - |的最大值.
8.在同一平面直角坐标系中,将曲线x2-36y2-8x+12=0变成曲线x′2-y′2-4x′+3=0,求满足条件的伸缩变换.
9.在平面直角坐标系中,求下列方程所对应的图形经
过伸缩变换 后的图形是什么形状?
(1)y2=2x;
(2)x2+y2=1.
10.通过平面直角坐标系中的平移与伸缩变换,可以把
椭圆 + =1变为中心在原点的单位圆,求上述
平移变换与伸缩变换,以及这两种变换的合成变换.
12.有一种大型商品,A,B两地都有销售,且价格相同.某地居民从两地之一购得商品后,每千米回运A地的费用是B地的3倍.已知A,B两地相距10 km,顾客选A地或B地购买这件商品的标准是:运费和价格的总费用较低,求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.
分析:将问题看作数学中的不等关系,建立适当的坐标系,利用坐标法列式求解.
解析:如下图所示,以A、B所确定的直线为x轴,A、B中点O为坐标原点,建立直角坐标系,则A(-5,0)、B(5,0).设某地P的坐标为(x,y),且P地居民选择A地购买商品较便宜,并设A地的回运费为3a元/千米,B地的回运费为a元/千米.
13.求函数g(x)= + 的最小值.
解析:g(x)= + ,于是问题转化为在x轴上求一点P(x,0),使它分别到A(2,3)与B(5,1)的距离之和即|PA|+|PB|为最小值.
如上图所示,点B(5,1)关于x轴的对称点是B′(5,-1),故最小值为|AB′|,即g(x)的最小值为|AB′|= =5,而P点的位置就是直线AB′与x轴的交点.
1.直角坐标系可以有不同的建立方法,根据图形的几何特点选择适当的直角坐标系的一些规则:
(1)如果图形有对称中心,可以选对称中心为坐标原点.
(2)如果图形有对称轴,可以选对称轴为坐标轴.
(3)使图形上的特殊点尽可能多地在坐标轴上.
2.坐标系的建立是为了确定点的位置,在所创建的坐标系中,应满足:任意一点都有确定的坐标与它对应;反之,依据一个点的坐标就能确定这个点的位置.
3.坐标伸缩变换φ 注意变换中的系数均为正数;在伸缩变换下,平面直角坐标系保持不变,即在同一坐标系下只对点的坐标进行伸缩变换.
1.体会直角坐标系的作用,掌握平面直角坐标系中刻画点的位置的方法和坐标法的解题步骤.
2.会运用坐标法解决实际问题与几何问题.
3.通过具体例子,了解在平面直角坐标系伸缩变换作用下平面图形的变化情况及作用.
1.数轴
它使直线上任一点P都可以由唯一的实数x确定.
2.平面直角坐标系
在平面上,当取定两条互相垂直的直线的交点为原点,并确定度量单位和这两条直线的方向,就建立了平面直角坐标系.它使平面上任一点P都可以由唯一的实数对(x,y)确定.
练习
3.定义
设P(x,y)是平面直角坐标系中任意一点,在变换
的作用下,点P(x,y)对应P′(x′,y′) 称为平面直角坐标系中的伸缩变换.
练习
B
到直角坐标系两坐标轴距离相等的点的轨迹方程是____________.
答案:y=x或y=-x
平面内有一固定线段AB,|AB|=4,动点P满足|PA|-|PB|=3,O为AB中点,求|OP|的最小值.
解析:以AB的中点O为原点,AB所在直线为x轴建立平面直角坐标系,如下图,∵|PA|-|PB|=3<|AB|,则点P的轨迹是以点A、B为焦点的双曲线的右支上.
由题意知2c=4,∴c=2.
把方程y=sin x变为y′= sin 4x′的伸缩变换公式为________.
把圆X2+Y2=16沿x轴方向均匀压缩为椭圆x2+ =1,则坐标变换公式是________.
分析:利用平面直角坐标系中的坐标伸缩变换公式求解.
1.在?ABCD中三个顶点A、B、C的坐标分别是(-1,2)、(3,0)、(5,1),则点D的坐标是( )
A.(9,-1) B.(-3,1)
C.(1,3) D.(2,2)
C
B
A
4.两个定点距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹 .
答案:x2+y2=4
5.在△ABC中,B(-2,0),C(2,0),△ABC的周长为10,求点A的轨迹方程为________.
6.已知圆的半径为6,圆内一定点P离圆心的距离为4,A,B是圆上的两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.
解析:如右图所示,以圆心O为原点,OP所在直线为x轴建立直角坐标系,则圆的方程为x2+y2=36,P(4,0).
7.求函数g(x)=| - |的最大值.
8.在同一平面直角坐标系中,将曲线x2-36y2-8x+12=0变成曲线x′2-y′2-4x′+3=0,求满足条件的伸缩变换.
9.在平面直角坐标系中,求下列方程所对应的图形经
过伸缩变换 后的图形是什么形状?
(1)y2=2x;
(2)x2+y2=1.
10.通过平面直角坐标系中的平移与伸缩变换,可以把
椭圆 + =1变为中心在原点的单位圆,求上述
平移变换与伸缩变换,以及这两种变换的合成变换.
12.有一种大型商品,A,B两地都有销售,且价格相同.某地居民从两地之一购得商品后,每千米回运A地的费用是B地的3倍.已知A,B两地相距10 km,顾客选A地或B地购买这件商品的标准是:运费和价格的总费用较低,求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.
分析:将问题看作数学中的不等关系,建立适当的坐标系,利用坐标法列式求解.
解析:如下图所示,以A、B所确定的直线为x轴,A、B中点O为坐标原点,建立直角坐标系,则A(-5,0)、B(5,0).设某地P的坐标为(x,y),且P地居民选择A地购买商品较便宜,并设A地的回运费为3a元/千米,B地的回运费为a元/千米.
13.求函数g(x)= + 的最小值.
解析:g(x)= + ,于是问题转化为在x轴上求一点P(x,0),使它分别到A(2,3)与B(5,1)的距离之和即|PA|+|PB|为最小值.
如上图所示,点B(5,1)关于x轴的对称点是B′(5,-1),故最小值为|AB′|,即g(x)的最小值为|AB′|= =5,而P点的位置就是直线AB′与x轴的交点.
1.直角坐标系可以有不同的建立方法,根据图形的几何特点选择适当的直角坐标系的一些规则:
(1)如果图形有对称中心,可以选对称中心为坐标原点.
(2)如果图形有对称轴,可以选对称轴为坐标轴.
(3)使图形上的特殊点尽可能多地在坐标轴上.
2.坐标系的建立是为了确定点的位置,在所创建的坐标系中,应满足:任意一点都有确定的坐标与它对应;反之,依据一个点的坐标就能确定这个点的位置.
3.坐标伸缩变换φ 注意变换中的系数均为正数;在伸缩变换下,平面直角坐标系保持不变,即在同一坐标系下只对点的坐标进行伸缩变换.
