一 平面直角坐标系 课件(38张PPT)
文档属性
| 名称 | 一 平面直角坐标系 课件(38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 922.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 07:53:05 | ||
图片预览







文档简介
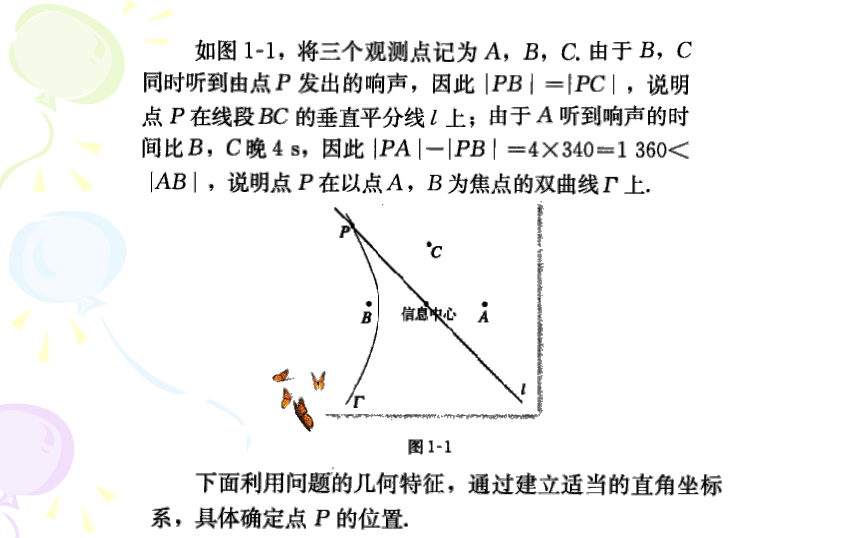
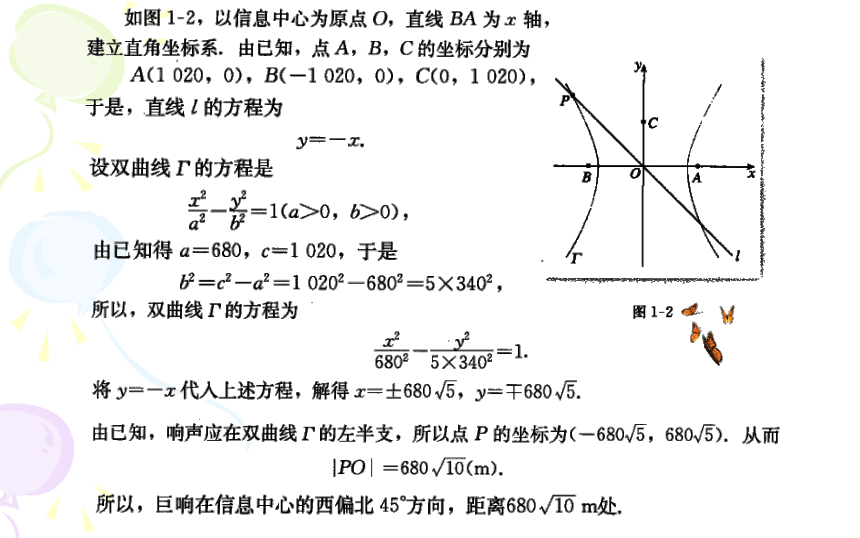
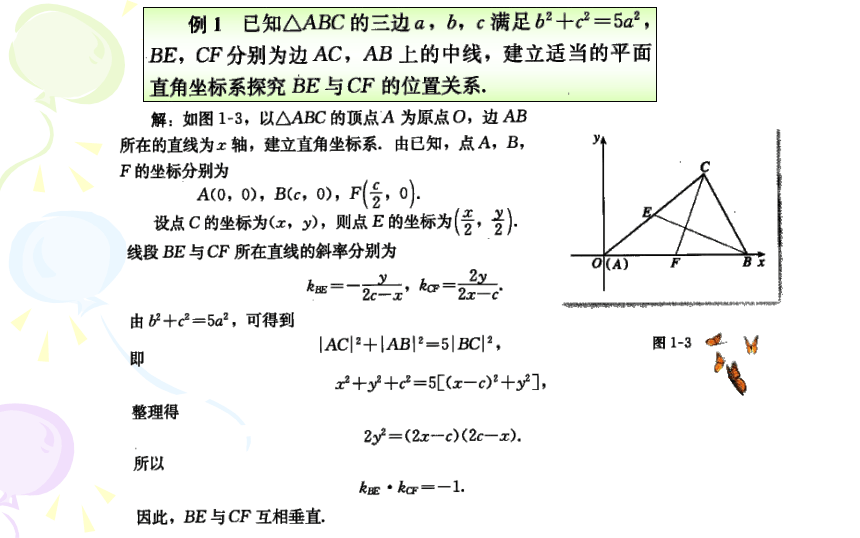
第一讲 坐标系
xxz
一、平面直角坐标系
1、平面直角坐标系
思考:
思考:
思考:
探究
根据几何特点选择适当的直角坐标系的一些规则:
(1)如果图形有对称中心,可以选择对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能地在坐标轴上。
x
O
?
2?
y=sinx
y=sin2x
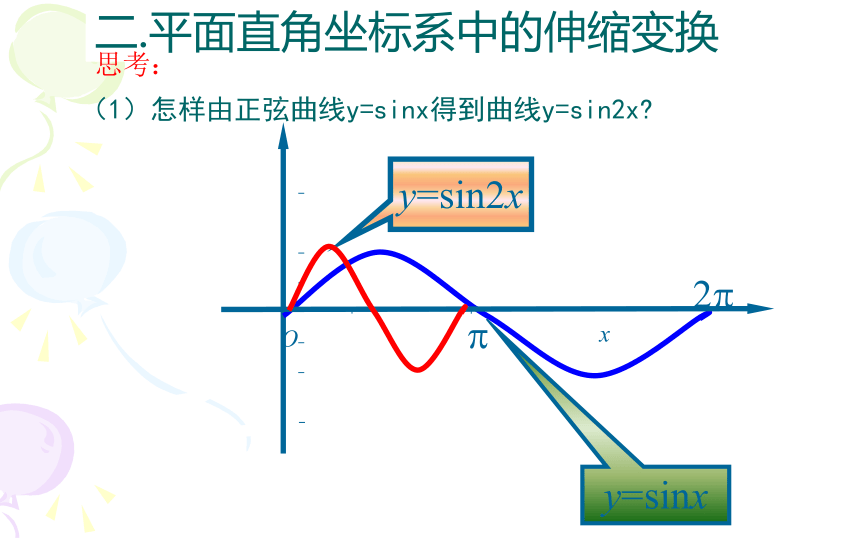
二.平面直角坐标系中的伸缩变换
思考:
(1)怎样由正弦曲线y=sinx得到曲线y=sin2x?
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,就得到正弦曲线y=sin2x.
通常把 叫做平面直角坐标系中的一个压缩变换。
1
坐标对应关系为:
1
上述的变换实质上就是一个坐标的压缩变换,即:
设P(x,y)是平面直角坐标系中任意一点,保持纵坐标不变,将横坐标x缩为原来 ,得到点
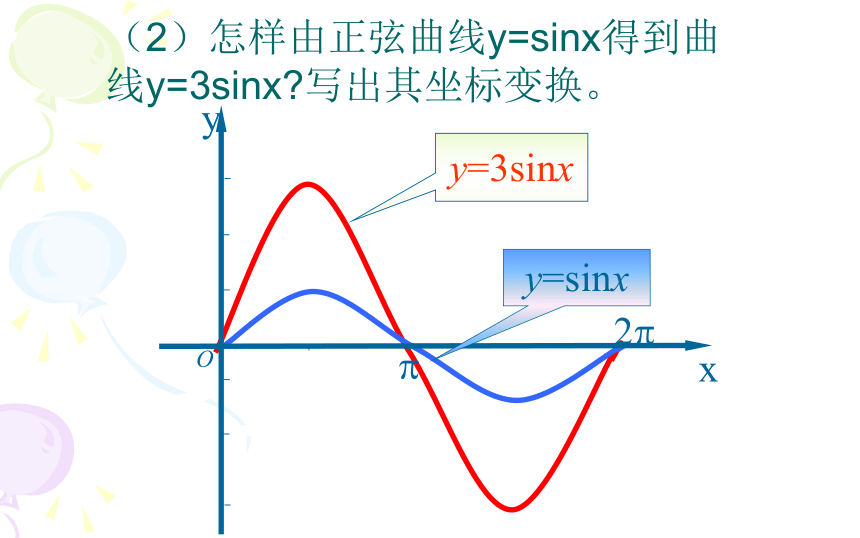
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。
O
?
2?
y=sinx
y=3sinx
y
x
在正弦曲线上任取一点P(x,y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。
通常把 叫做平面直角坐标系中的一个坐标伸长变换。
2
2
设点P(x,y)经变换得到点为
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写出其坐标变换。
O
?
2?
y=sinx
y=3sin2x
y
x
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x.
设点P(x,y)经变换得到点为
通常把 叫做平面直角坐标系中的一个坐标伸缩变换。
3
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写出其坐标变换。
3
定义:设P(x,y)是平面直角坐标系中任意一点,在变换
的作用下,点P(x,y)对应 称
为平面直角坐标系中的伸缩变换。
4
注 (1)
(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
例2:在直角坐标系中,求下列方程所对应的图形经过伸缩变换
后的图形。
(1)2x+3y=0; (2)x2+y2=1
1.在同一直角坐标系下,求满足下列图形的伸缩变换:
曲线4x2+9y2=36变为曲线
2.在同一直角坐标系下经过伸缩变换 后,
曲线C变为 ,求曲线C的方程并画出图形。
课堂小结:
(1)体会坐标法的思想,应用坐标法解决几何问题;
(2)掌握平面直角坐标系中的伸缩变换。
思考题
选修4-4第一讲
极坐标系
从这里向东北走
500米就到了
请问:去省实验
中学怎么走?
问路人
好心人
请认真分析好心人的回答:“从这里向东北走500米就到了”,他是从哪些方面确定省实验中学位置的?
在我们日常生活中人们经常用方向和距离来确定一点的位置,这种用方向和距离确定平面上一点位置的思想,就是极坐标的基本思想。
出发点、方向、距离
请大家回忆直角坐标系的建立过程,试着建立一个用距离与角度确定平面上一点位置的坐标系.
试一试?
一、极坐标系的建立:
在平面内取一个定点 ,叫做极点;
引一条射线 ,叫做极轴;
再选定一个长度单位和角度单位(通常取弧度)及它的正方向(通常取逆时针方向),
这样就建立了一个极坐标系。
X
O
如图:极坐标系OX,对比直角坐标系想一想平面上任意一点M的极坐标该如何表示?
X
O
M.
?
?
想一想?
记:M(?,?)
强调:不做特殊说明时,?≥0,?∈R 当?=0时,表示极点。
?表示线段OM的长度,叫做点M的极径;
X
O
M.
?
?
有序数对(?,?)就叫做点M的极坐标.
?表示以OX为始边,射线OM为终边的
角,叫做点M的极角;
2.极坐标平面上一个定点M(?,?)的
极坐标是否可以写出统一的表达
式?
思考?
1.在极坐标平面上点与坐标的对应关系是怎样的?
3.若使极坐标平面上点与坐标也为一一对应关系需增加什么条件?
例1:说出图中点A、B、C的极 坐标,并标出点 所在的位置.
例2:下图是某校园的平面示意图,点
A,B,C,D,E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置,建立适当的极坐标系,写出各点的极坐标。
50m
B
D
E
C
A
60m
120m
45o
60o
O
X
平面内一点P的直角坐标是 ,其极坐标如何表示?点Q的极坐标为 ,其直角坐标如何表示?
思考?
答案:
三、极坐标与直角坐标的互化
公式
例3:互化下列直角坐标与极坐标
直角坐标
极坐标
直角坐标
极坐标
2、已知极坐标系中两点 ,
如何求线段|PQ|的长?
推广:极坐标系内两点 的距离公式:
探索?
1、极坐标系中点的对称关系?
四、课堂练习
2.已知三点的极坐标为
,则 为( )
A、正三角形 B、直角三角形
C、锐角等腰三角形 D、等腰直角三角形
1.已知极坐标 ,下列所给出的
不能表示点M的坐标的是( )
C
D
)
3
,
5
(
p
-
、
C
3、极坐标与直角坐标的互化公式
小 结
1、极坐标系的四要素
2、点与其极坐标一一对应的条件
极点;极轴;长度单位;角度单位
及它的正方向。
思考题:
1.极坐标方程 表示什么图形?
2.极坐标方程 表示什么图形?
呢?
xxz
一、平面直角坐标系
1、平面直角坐标系
思考:
思考:
思考:
探究
根据几何特点选择适当的直角坐标系的一些规则:
(1)如果图形有对称中心,可以选择对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能地在坐标轴上。
x
O
?
2?
y=sinx
y=sin2x
二.平面直角坐标系中的伸缩变换
思考:
(1)怎样由正弦曲线y=sinx得到曲线y=sin2x?
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,就得到正弦曲线y=sin2x.
通常把 叫做平面直角坐标系中的一个压缩变换。
1
坐标对应关系为:
1
上述的变换实质上就是一个坐标的压缩变换,即:
设P(x,y)是平面直角坐标系中任意一点,保持纵坐标不变,将横坐标x缩为原来 ,得到点
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。
O
?
2?
y=sinx
y=3sinx
y
x
在正弦曲线上任取一点P(x,y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。
通常把 叫做平面直角坐标系中的一个坐标伸长变换。
2
2
设点P(x,y)经变换得到点为
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写出其坐标变换。
O
?
2?
y=sinx
y=3sin2x
y
x
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x.
设点P(x,y)经变换得到点为
通常把 叫做平面直角坐标系中的一个坐标伸缩变换。
3
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写出其坐标变换。
3
定义:设P(x,y)是平面直角坐标系中任意一点,在变换
的作用下,点P(x,y)对应 称
为平面直角坐标系中的伸缩变换。
4
注 (1)
(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
例2:在直角坐标系中,求下列方程所对应的图形经过伸缩变换
后的图形。
(1)2x+3y=0; (2)x2+y2=1
1.在同一直角坐标系下,求满足下列图形的伸缩变换:
曲线4x2+9y2=36变为曲线
2.在同一直角坐标系下经过伸缩变换 后,
曲线C变为 ,求曲线C的方程并画出图形。
课堂小结:
(1)体会坐标法的思想,应用坐标法解决几何问题;
(2)掌握平面直角坐标系中的伸缩变换。
思考题
选修4-4第一讲
极坐标系
从这里向东北走
500米就到了
请问:去省实验
中学怎么走?
问路人
好心人
请认真分析好心人的回答:“从这里向东北走500米就到了”,他是从哪些方面确定省实验中学位置的?
在我们日常生活中人们经常用方向和距离来确定一点的位置,这种用方向和距离确定平面上一点位置的思想,就是极坐标的基本思想。
出发点、方向、距离
请大家回忆直角坐标系的建立过程,试着建立一个用距离与角度确定平面上一点位置的坐标系.
试一试?
一、极坐标系的建立:
在平面内取一个定点 ,叫做极点;
引一条射线 ,叫做极轴;
再选定一个长度单位和角度单位(通常取弧度)及它的正方向(通常取逆时针方向),
这样就建立了一个极坐标系。
X
O
如图:极坐标系OX,对比直角坐标系想一想平面上任意一点M的极坐标该如何表示?
X
O
M.
?
?
想一想?
记:M(?,?)
强调:不做特殊说明时,?≥0,?∈R 当?=0时,表示极点。
?表示线段OM的长度,叫做点M的极径;
X
O
M.
?
?
有序数对(?,?)就叫做点M的极坐标.
?表示以OX为始边,射线OM为终边的
角,叫做点M的极角;
2.极坐标平面上一个定点M(?,?)的
极坐标是否可以写出统一的表达
式?
思考?
1.在极坐标平面上点与坐标的对应关系是怎样的?
3.若使极坐标平面上点与坐标也为一一对应关系需增加什么条件?
例1:说出图中点A、B、C的极 坐标,并标出点 所在的位置.
例2:下图是某校园的平面示意图,点
A,B,C,D,E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置,建立适当的极坐标系,写出各点的极坐标。
50m
B
D
E
C
A
60m
120m
45o
60o
O
X
平面内一点P的直角坐标是 ,其极坐标如何表示?点Q的极坐标为 ,其直角坐标如何表示?
思考?
答案:
三、极坐标与直角坐标的互化
公式
例3:互化下列直角坐标与极坐标
直角坐标
极坐标
直角坐标
极坐标
2、已知极坐标系中两点 ,
如何求线段|PQ|的长?
推广:极坐标系内两点 的距离公式:
探索?
1、极坐标系中点的对称关系?
四、课堂练习
2.已知三点的极坐标为
,则 为( )
A、正三角形 B、直角三角形
C、锐角等腰三角形 D、等腰直角三角形
1.已知极坐标 ,下列所给出的
不能表示点M的坐标的是( )
C
D
)
3
,
5
(
p
-
、
C
3、极坐标与直角坐标的互化公式
小 结
1、极坐标系的四要素
2、点与其极坐标一一对应的条件
极点;极轴;长度单位;角度单位
及它的正方向。
思考题:
1.极坐标方程 表示什么图形?
2.极坐标方程 表示什么图形?
呢?
