极坐标系 课件(18张PPT)
文档属性
| 名称 | 极坐标系 课件(18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 264.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 07:53:56 | ||
图片预览





文档简介
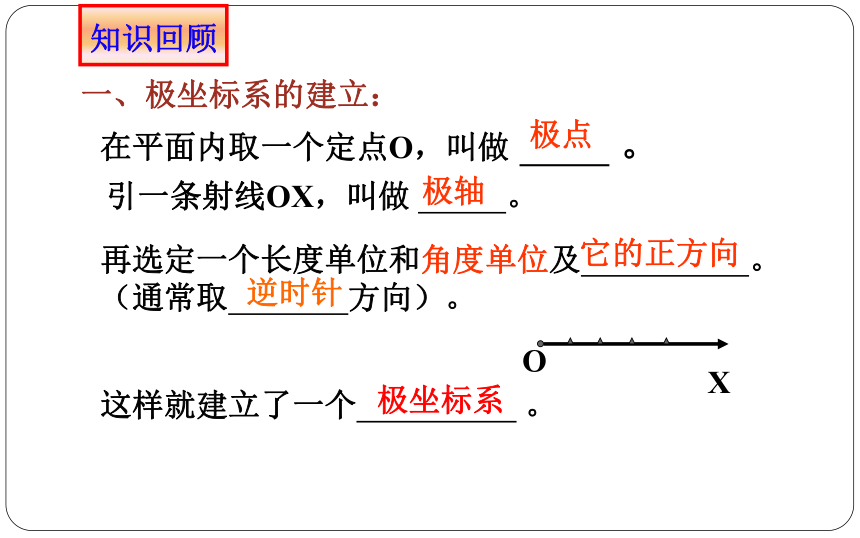
一、极坐标系的建立:
在平面内取一个定点O,叫做 。
引一条射线OX,叫做 。
再选定一个长度单位和角度单位及 。(通常取 方向)。
这样就建立了一个 。
X
O
知识回顾
极点
极轴
它的正方向
逆时针
极坐标系
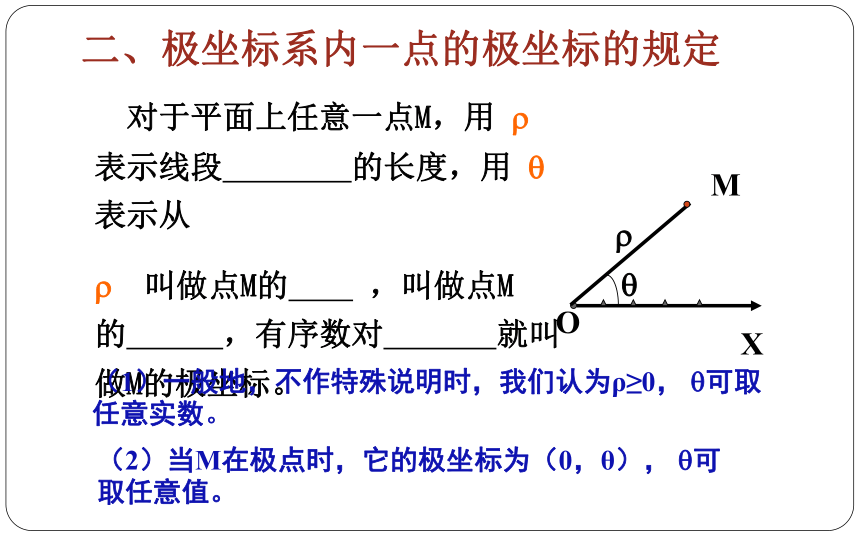
二、极坐标系内一点的极坐标的规定
X
O
M
?
?
对于平面上任意一点M,用 ? 表示线段 的长度,用 ? 表示从
? 叫做点M的 ,叫做点M的 ,有序数对 就叫做M的极坐标。
(1)一般地,不作特殊说明时,我们认为ρ≥0, ?可取任意实数。
(2)当M在极点时,它的极坐标为(0,θ), ?可取任意值。
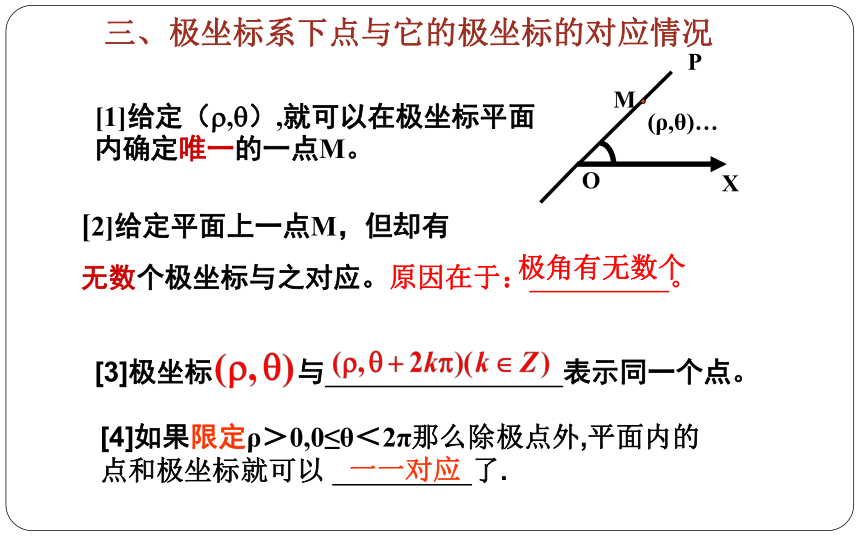
三、极坐标系下点与它的极坐标的对应情况
[1]给定(?,?),就可以在极坐标平面内确定唯一的一点M。
[2]给定平面上一点M,但却有
无数个极坐标与之对应。原因在于: 。
O
X
P
M
(ρ,θ)…
[4]如果限定ρ>0,0≤θ<2π那么除极点外,平面内的点和极坐标就可以 了.
极角有无数个
[3]极坐标 与 表示同一个点。
一一对应
1).在直角坐标系下:
(1)给定(?,?),就可以在极坐标平面内确定唯一的一点M。
(2)给定平面上一点M,但却有无数个极坐标与之对应。
能否附加限定条件使平面内的点和极坐标一一对应呢?
极坐标与直角坐标在刻画点的位置时有何区别?
思考:
点 坐标(x,y)
一一对应
2).极坐标系下:
O
X
M
(ρ,θ)
反思
限定条件ρ>0,0≤θ<2π
你能把点的直角坐标和极坐标进行互相转化么?
1.2.2极直互化
思考:
平面内的一个点的直角坐标是(1, )
这个点如何用极坐标表示?
在直角坐标系中,
以原点作为极点,
x轴的正半轴作为极轴,
并且两种坐标系中取
相同的长度单位
点M的直角坐标为
O
x
y
θ
设点M的极坐标为(ρ,θ)
极坐标与直角坐标的互化关系式:
设点M的直角坐标是 (x, y)
极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合;
2. 极轴与直角坐标系的x轴的正半轴重合;
3. 两种坐标系的单位长度相同.
正弦、余弦、正切的三角函数值
θ
sinθ
cosθ
tanθ
知识回顾
例1. 将点M的极坐标
化成直角坐标.
解:
所以, 点M的直角坐标为
已知下列点的极坐标,求它们的直
角坐标。
例2. 将点M的直角坐标
化成极坐标.
解:
因为点在第三象限, 所以
因此, 点M的极坐标为
练习: 已知点的直角坐标, 求它们
的极坐标.
1、已知A(3, ),B(4, ),求线段AB
的长度。
潜能开发:
除了你已经使用的方法以外,你还会用其他方法解决么?
如果上题中的坐标改为A(3, ),B(5, )呢?
变式:
探讨:
你能给出极坐标系下的两点间的距离公式么?
| |
AB
=
则
若
2、已知在极坐标中A(2, ),B(4, ),
求 的面积。
极坐标与直角坐标的互化关系式:
设点M的直角坐标是 (x, y)
极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
课堂小结
在平面内取一个定点O,叫做 。
引一条射线OX,叫做 。
再选定一个长度单位和角度单位及 。(通常取 方向)。
这样就建立了一个 。
X
O
知识回顾
极点
极轴
它的正方向
逆时针
极坐标系
二、极坐标系内一点的极坐标的规定
X
O
M
?
?
对于平面上任意一点M,用 ? 表示线段 的长度,用 ? 表示从
? 叫做点M的 ,叫做点M的 ,有序数对 就叫做M的极坐标。
(1)一般地,不作特殊说明时,我们认为ρ≥0, ?可取任意实数。
(2)当M在极点时,它的极坐标为(0,θ), ?可取任意值。
三、极坐标系下点与它的极坐标的对应情况
[1]给定(?,?),就可以在极坐标平面内确定唯一的一点M。
[2]给定平面上一点M,但却有
无数个极坐标与之对应。原因在于: 。
O
X
P
M
(ρ,θ)…
[4]如果限定ρ>0,0≤θ<2π那么除极点外,平面内的点和极坐标就可以 了.
极角有无数个
[3]极坐标 与 表示同一个点。
一一对应
1).在直角坐标系下:
(1)给定(?,?),就可以在极坐标平面内确定唯一的一点M。
(2)给定平面上一点M,但却有无数个极坐标与之对应。
能否附加限定条件使平面内的点和极坐标一一对应呢?
极坐标与直角坐标在刻画点的位置时有何区别?
思考:
点 坐标(x,y)
一一对应
2).极坐标系下:
O
X
M
(ρ,θ)
反思
限定条件ρ>0,0≤θ<2π
你能把点的直角坐标和极坐标进行互相转化么?
1.2.2极直互化
思考:
平面内的一个点的直角坐标是(1, )
这个点如何用极坐标表示?
在直角坐标系中,
以原点作为极点,
x轴的正半轴作为极轴,
并且两种坐标系中取
相同的长度单位
点M的直角坐标为
O
x
y
θ
设点M的极坐标为(ρ,θ)
极坐标与直角坐标的互化关系式:
设点M的直角坐标是 (x, y)
极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合;
2. 极轴与直角坐标系的x轴的正半轴重合;
3. 两种坐标系的单位长度相同.
正弦、余弦、正切的三角函数值
θ
sinθ
cosθ
tanθ
知识回顾
例1. 将点M的极坐标
化成直角坐标.
解:
所以, 点M的直角坐标为
已知下列点的极坐标,求它们的直
角坐标。
例2. 将点M的直角坐标
化成极坐标.
解:
因为点在第三象限, 所以
因此, 点M的极坐标为
练习: 已知点的直角坐标, 求它们
的极坐标.
1、已知A(3, ),B(4, ),求线段AB
的长度。
潜能开发:
除了你已经使用的方法以外,你还会用其他方法解决么?
如果上题中的坐标改为A(3, ),B(5, )呢?
变式:
探讨:
你能给出极坐标系下的两点间的距离公式么?
| |
AB
=
则
若
2、已知在极坐标中A(2, ),B(4, ),
求 的面积。
极坐标与直角坐标的互化关系式:
设点M的直角坐标是 (x, y)
极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
课堂小结
