1.2 极坐标系 课件(32张PPT)
文档属性
| 名称 | 1.2 极坐标系 课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 988.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 07:55:03 | ||
图片预览











文档简介
极 坐 标 系
1.理解极坐标的概念.
2.能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别.
1.极坐标系的建立
在平面上取一个定点O,自点O引一条射线Ox,同时确定一个单位长度和计算角度的正方向(通常取逆时针方向为正方向),这样就建立了一个极坐标系(其中O称为极点,射线Ox称为极轴).
2.极坐标系内一点的极坐标的规定
对于平面上任意一点M,用ρ表示线段OM的长度,用θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫做M的极坐标.
特别强调:由极径的意义可知,ρ≥0;当极角θ的取值范围是[0,2π)时,平面上的点(除去极点)就与极坐标(ρ,θ)建立一一对应的关系.
3.负极径的规定
在极坐标系中,极径ρ允许取负值,极角θ也可以取任意的正角或负角.
当ρ<0时,点M(ρ,θ)位于极角终边的反向延长线上,且OM=|ρ|.
一般地,极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一个点,和直角坐标系不同,平面内一个点的极坐标有无数种表示.?
约定:极点的极坐标是ρ=0,θ可以取任意角.
4.直角坐标与极坐标的互化
以直角坐标系的O为极点,x轴正半轴为极轴,且在两坐标系中取相同的单位长度,平面内的任一点P的直角坐标和极坐标分别为(x,y)和(ρ,θ),则
或
5.互化公式的前提条件:?
①极点与直角坐标系原点重合;?
②极轴与直角坐标系正半轴重合;?
③两种坐标系的单位长度相同.?
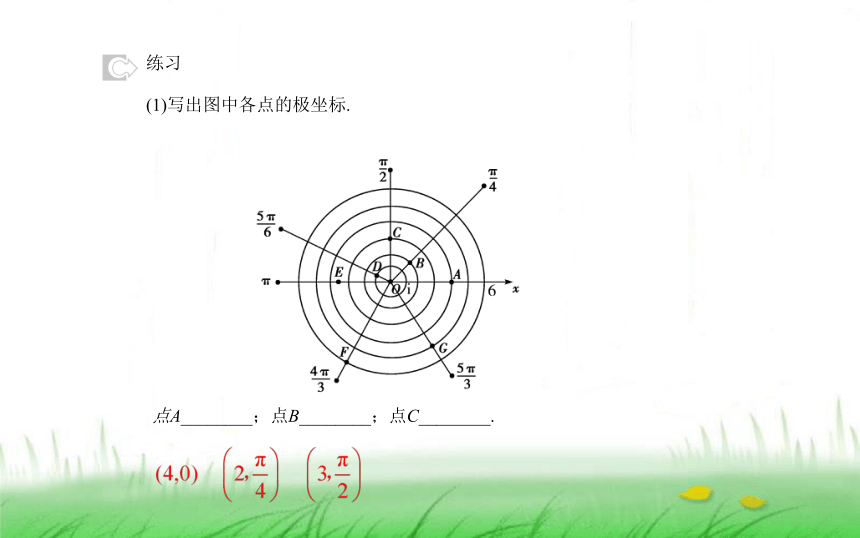
练习
点A________;点B________;点C________.
(1)写出图中各点的极坐标.
(2)回答下列问题:
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由什么引起的?
答案:(1)不是 (2)无数种表示方法 (3)由极角的多值性引起
D
练习
把点M的极坐标 化成直角坐标.
答案:(-4,4 )
写出图中各点的极坐标(ρ>0,0≤θ<2π).
分析:根据极坐标定义:若M是平面上任一点,ρ表示OM的长度,θ表示以射线Ox为始边,射线OM为终边所成的角.
B
C
B
C
5.把点M的极坐标 化为直角坐标形式.
6.已知圆C:(x+1)2+(y- )2=1,则圆心C的极坐标为________(ρ>0,0≤θ<2π).
7.极坐标系中,点A的极坐标是 ,则:
(1)点A关于极轴对称的点的极坐标是________.
(2)点A关于极点对称的点的极坐标是________.
(3)点A关于直线θ= 的对称点的极坐标是_____. (限定ρ>0,θ∈[0,2π).)
8.直线l过点A ,B ,则直线l与极轴的夹角等于________.
9.把点M的直角坐标(1,-1)化为极坐标形式(限定r≥0,-p
10.将下列各点的极坐标化为直角坐标形式.
(1) . (2) .(3)(5,π).
11.将下列各点的直角坐标化为极坐标(ρ>0,0≤θ<2π).
(1)( ,3). (2)(-1,-1). (3)(-3,0).
12.在极轴上求与点A 的距离为5的点M的坐标.
13.已知点Q(ρ,θ),分别按下列条件求出点P的极坐标.
(1)点P是点Q关于极点O的对称点.
(2)点P是点Q关于直线θ= 的对称点.
分析:通过数形结合,确定P点的极径与极角.
解析:(1)由于P、Q关于极点对称,得它们的极径|OP|=|OQ|,极角相差(2k+1)p(k∈Z).所以,点P的极坐标为(r,(2k+1)p+q)或(-r,(2kp+q)(k∈Z).
(2)由P、Q关于直线q+ 对称,得它们的极径|OP|= |OQ|,点P的极角q′满足
q′=p-q+2kp(k∈Z),
所以点P的坐标为:
(r,(2k+1)p-q)或(-r,2kp-q)(k∈Z).
1.极坐标系的四要素:①极点;②极轴;③长度单位;?④角?度单位和它的正方向.四者缺一不可.?
2.由极径的意义,知ρ≥0.当极角θ的取值范围是[0,2π)时,平面上的点(除去极点)与极坐标(ρ,θ)(ρ≠0)建立一一对应的关系.约定:极点的极坐标是极径ρ=0时,极角可以取任意角.?
3.极坐标与直角坐标的重要区别是多值性.在直角坐标系中,点与直角坐标是“一对一”的关系;在极坐标系中,由于终边相同的角有无数个,即点的极角不唯一,因此点与极点是“一对多”的关系.但不同的极坐标可以写出统一的表达式.如果(ρ,θ)是点M的极坐标,那么(ρ,θ+2kπ)或(-ρ,θ+(2k+1)π)(k∈Z)都可以作为点M的极坐标,但这样建立的极坐标系,平面上的点与它的极坐标之间就不是一一对应关系.
1.理解极坐标的概念.
2.能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别.
1.极坐标系的建立
在平面上取一个定点O,自点O引一条射线Ox,同时确定一个单位长度和计算角度的正方向(通常取逆时针方向为正方向),这样就建立了一个极坐标系(其中O称为极点,射线Ox称为极轴).
2.极坐标系内一点的极坐标的规定
对于平面上任意一点M,用ρ表示线段OM的长度,用θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫做M的极坐标.
特别强调:由极径的意义可知,ρ≥0;当极角θ的取值范围是[0,2π)时,平面上的点(除去极点)就与极坐标(ρ,θ)建立一一对应的关系.
3.负极径的规定
在极坐标系中,极径ρ允许取负值,极角θ也可以取任意的正角或负角.
当ρ<0时,点M(ρ,θ)位于极角终边的反向延长线上,且OM=|ρ|.
一般地,极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一个点,和直角坐标系不同,平面内一个点的极坐标有无数种表示.?
约定:极点的极坐标是ρ=0,θ可以取任意角.
4.直角坐标与极坐标的互化
以直角坐标系的O为极点,x轴正半轴为极轴,且在两坐标系中取相同的单位长度,平面内的任一点P的直角坐标和极坐标分别为(x,y)和(ρ,θ),则
或
5.互化公式的前提条件:?
①极点与直角坐标系原点重合;?
②极轴与直角坐标系正半轴重合;?
③两种坐标系的单位长度相同.?
练习
点A________;点B________;点C________.
(1)写出图中各点的极坐标.
(2)回答下列问题:
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由什么引起的?
答案:(1)不是 (2)无数种表示方法 (3)由极角的多值性引起
D
练习
把点M的极坐标 化成直角坐标.
答案:(-4,4 )
写出图中各点的极坐标(ρ>0,0≤θ<2π).
分析:根据极坐标定义:若M是平面上任一点,ρ表示OM的长度,θ表示以射线Ox为始边,射线OM为终边所成的角.
B
C
B
C
5.把点M的极坐标 化为直角坐标形式.
6.已知圆C:(x+1)2+(y- )2=1,则圆心C的极坐标为________(ρ>0,0≤θ<2π).
7.极坐标系中,点A的极坐标是 ,则:
(1)点A关于极轴对称的点的极坐标是________.
(2)点A关于极点对称的点的极坐标是________.
(3)点A关于直线θ= 的对称点的极坐标是_____. (限定ρ>0,θ∈[0,2π).)
8.直线l过点A ,B ,则直线l与极轴的夹角等于________.
9.把点M的直角坐标(1,-1)化为极坐标形式(限定r≥0,-p
10.将下列各点的极坐标化为直角坐标形式.
(1) . (2) .(3)(5,π).
11.将下列各点的直角坐标化为极坐标(ρ>0,0≤θ<2π).
(1)( ,3). (2)(-1,-1). (3)(-3,0).
12.在极轴上求与点A 的距离为5的点M的坐标.
13.已知点Q(ρ,θ),分别按下列条件求出点P的极坐标.
(1)点P是点Q关于极点O的对称点.
(2)点P是点Q关于直线θ= 的对称点.
分析:通过数形结合,确定P点的极径与极角.
解析:(1)由于P、Q关于极点对称,得它们的极径|OP|=|OQ|,极角相差(2k+1)p(k∈Z).所以,点P的极坐标为(r,(2k+1)p+q)或(-r,(2kp+q)(k∈Z).
(2)由P、Q关于直线q+ 对称,得它们的极径|OP|= |OQ|,点P的极角q′满足
q′=p-q+2kp(k∈Z),
所以点P的坐标为:
(r,(2k+1)p-q)或(-r,2kp-q)(k∈Z).
1.极坐标系的四要素:①极点;②极轴;③长度单位;?④角?度单位和它的正方向.四者缺一不可.?
2.由极径的意义,知ρ≥0.当极角θ的取值范围是[0,2π)时,平面上的点(除去极点)与极坐标(ρ,θ)(ρ≠0)建立一一对应的关系.约定:极点的极坐标是极径ρ=0时,极角可以取任意角.?
3.极坐标与直角坐标的重要区别是多值性.在直角坐标系中,点与直角坐标是“一对一”的关系;在极坐标系中,由于终边相同的角有无数个,即点的极角不唯一,因此点与极点是“一对多”的关系.但不同的极坐标可以写出统一的表达式.如果(ρ,θ)是点M的极坐标,那么(ρ,θ+2kπ)或(-ρ,θ+(2k+1)π)(k∈Z)都可以作为点M的极坐标,但这样建立的极坐标系,平面上的点与它的极坐标之间就不是一一对应关系.
