1.2 极坐标系 课件(23张PPT)
文档属性
| 名称 | 1.2 极坐标系 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 555.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 07:56:53 | ||
图片预览







文档简介
极坐标系
从这向北
2000米。
请问:去??
中学怎么走?
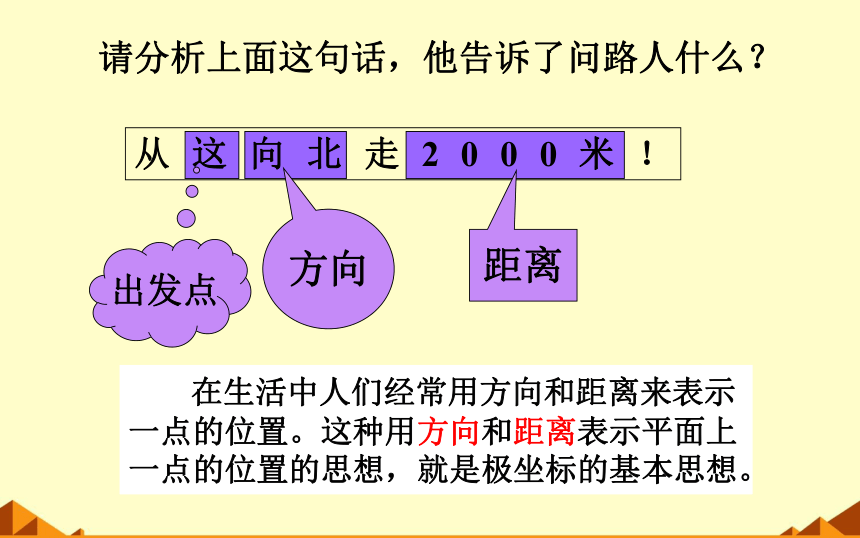
请分析上面这句话,他告诉了问路人什么?
从这向北走2000米!
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。
一、极坐标系的建立:
在平面内取一个定点O,叫做极点。
引一条射线OX,叫做极轴。
再选定一个长度单位和角度单位及它的正方向(通常取逆时针方向)。
这样就建立了一个极坐标系。
X
O
二、极坐标系内一点的极坐标的规定
X
O
M
?
?
对于平面上任意一点M,用 ? 表示线段OM的长度,用 ? 表示从OX到OM 的角度,? 叫做点M的极径, ?叫做点M的极角,有序数对(?,?)就叫做M的极坐标。
特别强调:?表示线段OM的长度,即点M到极点O的距离;?表示从OX到OM的角度,即以OX(极轴)为始边,OM 为终边的角。
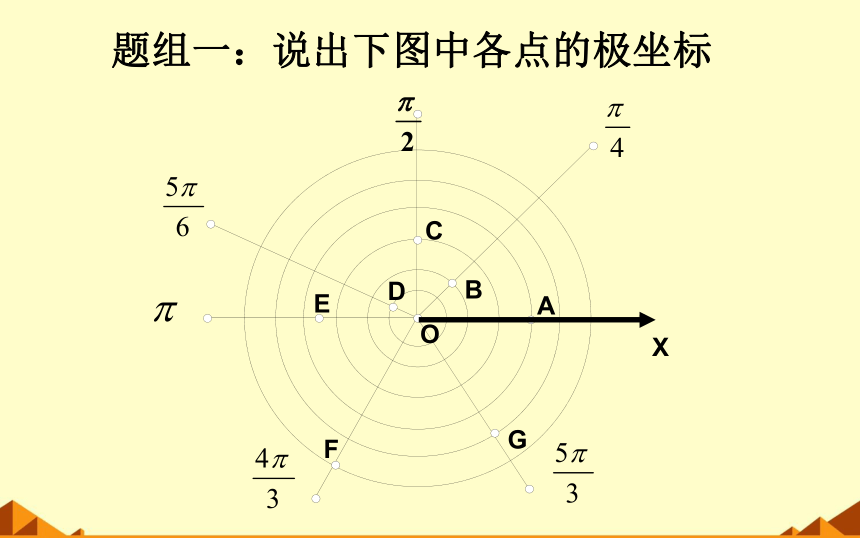
题组一:说出下图中各点的极坐标
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
特别规定: 当M在极点时,它的极坐标?=0,?可以取任意值。
想一想?
三、点的极坐标的表达式的研究
X
O
M
?
?
如图:OM的长度为4,
请说出点M的极坐标的其他表达式。
思考:这些极坐标之间有何异同?
思考:这些极角有何关系?
这些极角的始边相同,终边也相同。也就是说它们是终边相同的角。
点M的极坐标统一表达式:
极径相同,不同的是极角
题组二:在极坐标系里描出下列各点
A
B
C
D
E
F
G
O
X
四、极坐标系下点与它的极坐标的对应情况
[1]给定(?,?),就可以在极坐标平面内确定唯一的一点M。
[2]给定平面上一点M,但却有无数个极坐标与之对应。
原因在于:极角有无数个。
O
X
P
M
(ρ,θ)…
如果限定ρ>0,0≤θ<2π
那么除极点外,平面内的点和极坐标就可以一一对应了.
[3]一点的极坐标有否统一的表达式?
小结
[1]建立一个极坐标系需要哪些要素
极点;极轴;长度单位;角度单位和它的正方向。
[2]极坐标系内一点的极坐标有多少种表达式?
无数,极角有无数个。
有。(ρ,2kπ+θ)
极坐标和直角坐标的互化
平面内的一个点的直角坐标是(1, )
思 考:
这个点如何用极坐标表示?
O
x
y
在直角坐标系中,
以原点作为极点,
x轴的正半轴作为极轴,
并且两种坐标系中取相
同的长度单位
点M的直角坐标为
θ
设点M的极坐标为(ρ,θ)
M ( 2, ∏ / 3)
极坐标与直角坐标的互化关系式:
设点M的直角坐标是 (x, y)
极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合;
2. 极轴与直角坐标系的x轴的正半
轴重合;
3. 两种坐标系的单位长度相同.
例1. 将点M的极坐标
化成直角坐标.
解:
所以, 点M的直角坐标为
已知下列点的极坐标,求它们的直
角坐标。
例2. 将点M的直角坐标
化成极坐标.
解:
因为点在第三象限, 所以
因此, 点M的极坐标为
练习: 已知点的直角坐标, 求它们
的极坐标.
例3 已知两点(2, ),(3, )
求两点间的距离.
π
3
π
2
o
x
A
B
解:∠AOB =
π
6
用余弦定理求
AB的长即可.
从这向北
2000米。
请问:去??
中学怎么走?
请分析上面这句话,他告诉了问路人什么?
从这向北走2000米!
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。
一、极坐标系的建立:
在平面内取一个定点O,叫做极点。
引一条射线OX,叫做极轴。
再选定一个长度单位和角度单位及它的正方向(通常取逆时针方向)。
这样就建立了一个极坐标系。
X
O
二、极坐标系内一点的极坐标的规定
X
O
M
?
?
对于平面上任意一点M,用 ? 表示线段OM的长度,用 ? 表示从OX到OM 的角度,? 叫做点M的极径, ?叫做点M的极角,有序数对(?,?)就叫做M的极坐标。
特别强调:?表示线段OM的长度,即点M到极点O的距离;?表示从OX到OM的角度,即以OX(极轴)为始边,OM 为终边的角。
题组一:说出下图中各点的极坐标
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
特别规定: 当M在极点时,它的极坐标?=0,?可以取任意值。
想一想?
三、点的极坐标的表达式的研究
X
O
M
?
?
如图:OM的长度为4,
请说出点M的极坐标的其他表达式。
思考:这些极坐标之间有何异同?
思考:这些极角有何关系?
这些极角的始边相同,终边也相同。也就是说它们是终边相同的角。
点M的极坐标统一表达式:
极径相同,不同的是极角
题组二:在极坐标系里描出下列各点
A
B
C
D
E
F
G
O
X
四、极坐标系下点与它的极坐标的对应情况
[1]给定(?,?),就可以在极坐标平面内确定唯一的一点M。
[2]给定平面上一点M,但却有无数个极坐标与之对应。
原因在于:极角有无数个。
O
X
P
M
(ρ,θ)…
如果限定ρ>0,0≤θ<2π
那么除极点外,平面内的点和极坐标就可以一一对应了.
[3]一点的极坐标有否统一的表达式?
小结
[1]建立一个极坐标系需要哪些要素
极点;极轴;长度单位;角度单位和它的正方向。
[2]极坐标系内一点的极坐标有多少种表达式?
无数,极角有无数个。
有。(ρ,2kπ+θ)
极坐标和直角坐标的互化
平面内的一个点的直角坐标是(1, )
思 考:
这个点如何用极坐标表示?
O
x
y
在直角坐标系中,
以原点作为极点,
x轴的正半轴作为极轴,
并且两种坐标系中取相
同的长度单位
点M的直角坐标为
θ
设点M的极坐标为(ρ,θ)
M ( 2, ∏ / 3)
极坐标与直角坐标的互化关系式:
设点M的直角坐标是 (x, y)
极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合;
2. 极轴与直角坐标系的x轴的正半
轴重合;
3. 两种坐标系的单位长度相同.
例1. 将点M的极坐标
化成直角坐标.
解:
所以, 点M的直角坐标为
已知下列点的极坐标,求它们的直
角坐标。
例2. 将点M的直角坐标
化成极坐标.
解:
因为点在第三象限, 所以
因此, 点M的极坐标为
练习: 已知点的直角坐标, 求它们
的极坐标.
例3 已知两点(2, ),(3, )
求两点间的距离.
π
3
π
2
o
x
A
B
解:∠AOB =
π
6
用余弦定理求
AB的长即可.
