1.3 简单曲线的极坐标方程 课件(18张PPT)
文档属性
| 名称 | 1.3 简单曲线的极坐标方程 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 08:34:26 | ||
图片预览




文档简介
简单曲线的极坐标方程
问题提出
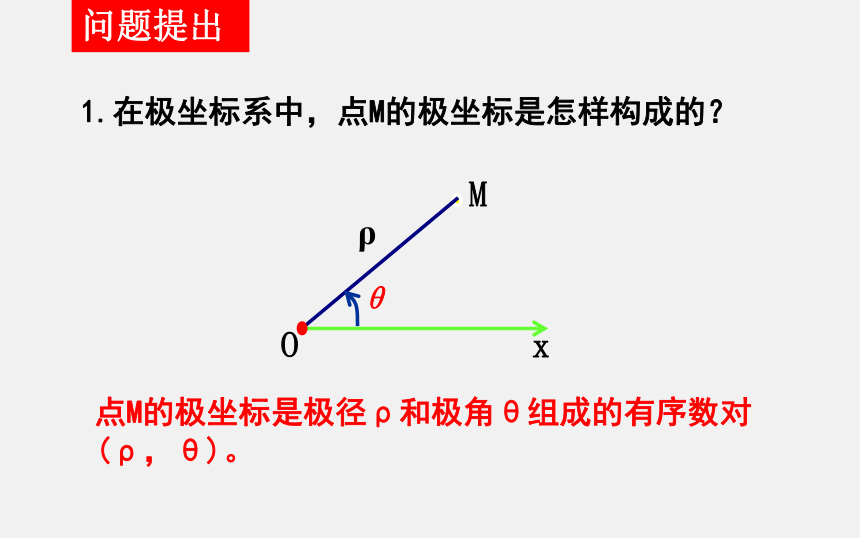
1.在极坐标系中,点M的极坐标是怎样构成的?
点M的极坐标是极径ρ和极角θ组成的有序数对(ρ,θ)。
ρ
θ
M
x
O
2.以直角坐标系原点O为极点,x轴正半轴为极轴建立极坐标系,则点M的直角坐标(x,y)与极坐标(ρ,θ)的互化公式是什么?
x=ρcosθ, y=ρsinθ.
3.在平面直角坐标系中,方程f(x,y)=0是曲线C的方程应具备的条件是什么?
(1)曲线C上任意一点的坐标都是方程f(x,y)=0的解;
(2)以方程f(x,y)=0的解为坐标的点都在曲线C上。
4.在极坐标系中,对一条曲线C,它也有相应的极坐标方程。因此,如何建立曲线的极坐标方程,如何根据曲线的极坐标方程分析曲线的有关性质,也就成为一个需要研究的课题。
探究:圆的极坐标方程
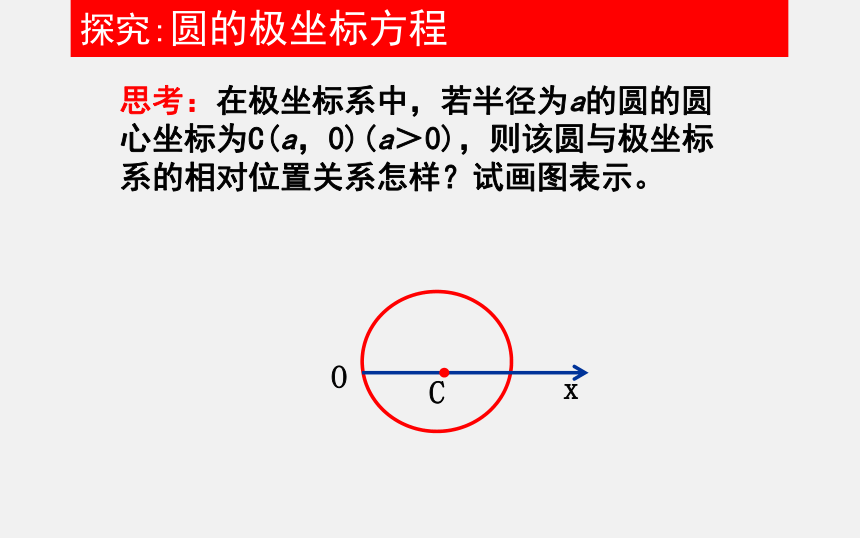
思考:在极坐标系中,若半径为a的圆的圆心坐标为C(a,0)(a>0),则该圆与极坐标系的相对位置关系怎样?试画图表示。
x
O
C
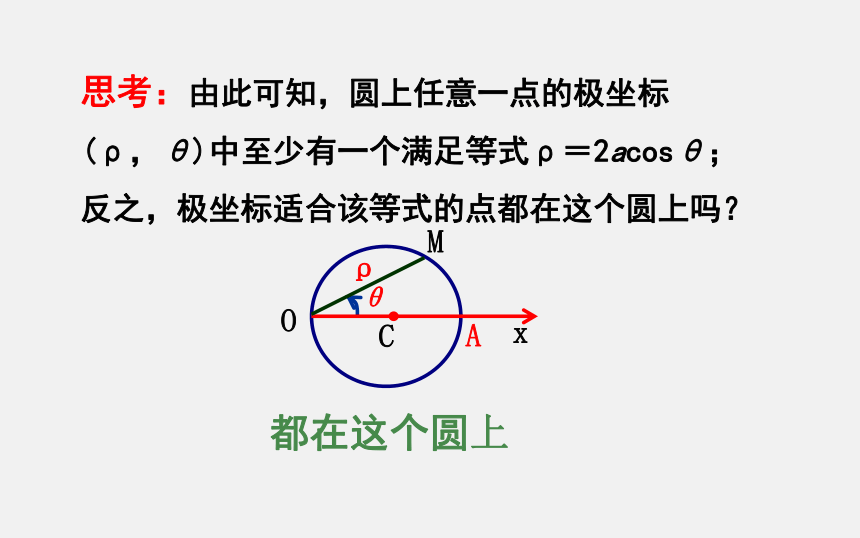
思考:设该圆与极轴的另一个交点为A,点M(ρ,θ)为圆上除点O,A以外的任意一点,那么极径ρ和极角θ之间满足什么关系?
M
θ
ρ
x
O
C
A
ρ=2acosθ
思考3:点O,A的极坐标可以分别是什么?它们都满足等式ρ=2a cosθ吗?
点 ,A(2a,0)都满足等式。
思考:由此可知,圆上任意一点的极坐标
(ρ,θ)中至少有一个满足等式ρ=2acosθ;
反之,极坐标适合该等式的点都在这个圆上吗?
都在这个圆上
M
θ
ρ
x
O
C
A
思考:等式ρ=2acosθ叫做圆C的极坐标方程。一般地,在极坐标系中,对于平面曲线C和方程f(ρ,θ)=0,在什么条件下,方程f(ρ,θ)=0是曲线C的极坐标方程?
(1)曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0;
(2)坐标适合方程f(ρ,θ)=0的点都在曲线C上。
思考:在极坐标系中,圆心坐标为C(a,π)(a>0),半径为a的圆的极坐标方程是什么?圆心坐标为C(a, )(a>0),半径为a的圆的极坐标方程是什么?
ρ=-2acosθ
ρ=2asinθ
M
θ
ρ
x
O
C
A
M
θ
ρ
x
O
C
A
思考:一般地,在极坐标系中,圆心坐标为C(a,α)(a>0),半径为r的圆的极坐标方程是什么?特别地,以极点为圆心,半径为r的圆的极坐标方程是什么?
M
θ
ρ
x
O
C
M
θ
ρ
x
O
ρ=r
思考:一般地,求曲线的极坐标方程的基本步骤是什么?
(1)建立极坐标系,设动点坐标;
(2)找出曲线上的点满足的几何条件;
(3)将几何条件用极坐标表示;
(4)化简小结。
下结论
建立极坐标系
设点(?,?)
找?,?的关系
化简 F(?,?)=0
练 习 1
求下列圆的极坐标方程
(1)中心在极点,半径为2;
(2)中心在C(a,0),半径为a;
(3)中心在(a,?/2),半径为a;
(4)中心在C(?0,?0),半径为r。
?=2
?=2acos ?
?=2asin ?
?2+ ?0 2 -2 ? ?0 cos( ?- ?0)= r2
极坐标方程分别是ρ=cosθ和ρ=sinθ的两个圆的圆心距是多少?
练 习 2
练习3
以极坐标系中的点(1,1)为圆心,1为半径的圆的方程是
C
3.极坐标方程
A.双曲线 B.椭圆 C.抛物线 D.圆
表示的曲线是( )
4.圆
的圆心坐标是( )
A. B. C. D.
B
B
小 结
a.在极坐标系中,点的极坐标是多值的,若点M在曲线C上,则点M的有些极坐标可能不适合曲线C的方程。
b. 圆的极坐标方程有多种形式,极坐标方程 可认为是圆的一般式方程。
(1)曲线的极坐标方程概念
(2)怎样求曲线的极坐标方程
( 3)圆的极坐标方程
极坐标方程与直角坐标方程可以相互转化,当研究对象与角和距离有关时,用极坐标方程解决比较方便,这是一个重要的解题技巧。在极坐标系中,当研究的问题用极坐标方程难以解决时,可转化为直角坐标方程求解。
问题提出
1.在极坐标系中,点M的极坐标是怎样构成的?
点M的极坐标是极径ρ和极角θ组成的有序数对(ρ,θ)。
ρ
θ
M
x
O
2.以直角坐标系原点O为极点,x轴正半轴为极轴建立极坐标系,则点M的直角坐标(x,y)与极坐标(ρ,θ)的互化公式是什么?
x=ρcosθ, y=ρsinθ.
3.在平面直角坐标系中,方程f(x,y)=0是曲线C的方程应具备的条件是什么?
(1)曲线C上任意一点的坐标都是方程f(x,y)=0的解;
(2)以方程f(x,y)=0的解为坐标的点都在曲线C上。
4.在极坐标系中,对一条曲线C,它也有相应的极坐标方程。因此,如何建立曲线的极坐标方程,如何根据曲线的极坐标方程分析曲线的有关性质,也就成为一个需要研究的课题。
探究:圆的极坐标方程
思考:在极坐标系中,若半径为a的圆的圆心坐标为C(a,0)(a>0),则该圆与极坐标系的相对位置关系怎样?试画图表示。
x
O
C
思考:设该圆与极轴的另一个交点为A,点M(ρ,θ)为圆上除点O,A以外的任意一点,那么极径ρ和极角θ之间满足什么关系?
M
θ
ρ
x
O
C
A
ρ=2acosθ
思考3:点O,A的极坐标可以分别是什么?它们都满足等式ρ=2a cosθ吗?
点 ,A(2a,0)都满足等式。
思考:由此可知,圆上任意一点的极坐标
(ρ,θ)中至少有一个满足等式ρ=2acosθ;
反之,极坐标适合该等式的点都在这个圆上吗?
都在这个圆上
M
θ
ρ
x
O
C
A
思考:等式ρ=2acosθ叫做圆C的极坐标方程。一般地,在极坐标系中,对于平面曲线C和方程f(ρ,θ)=0,在什么条件下,方程f(ρ,θ)=0是曲线C的极坐标方程?
(1)曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0;
(2)坐标适合方程f(ρ,θ)=0的点都在曲线C上。
思考:在极坐标系中,圆心坐标为C(a,π)(a>0),半径为a的圆的极坐标方程是什么?圆心坐标为C(a, )(a>0),半径为a的圆的极坐标方程是什么?
ρ=-2acosθ
ρ=2asinθ
M
θ
ρ
x
O
C
A
M
θ
ρ
x
O
C
A
思考:一般地,在极坐标系中,圆心坐标为C(a,α)(a>0),半径为r的圆的极坐标方程是什么?特别地,以极点为圆心,半径为r的圆的极坐标方程是什么?
M
θ
ρ
x
O
C
M
θ
ρ
x
O
ρ=r
思考:一般地,求曲线的极坐标方程的基本步骤是什么?
(1)建立极坐标系,设动点坐标;
(2)找出曲线上的点满足的几何条件;
(3)将几何条件用极坐标表示;
(4)化简小结。
下结论
建立极坐标系
设点(?,?)
找?,?的关系
化简 F(?,?)=0
练 习 1
求下列圆的极坐标方程
(1)中心在极点,半径为2;
(2)中心在C(a,0),半径为a;
(3)中心在(a,?/2),半径为a;
(4)中心在C(?0,?0),半径为r。
?=2
?=2acos ?
?=2asin ?
?2+ ?0 2 -2 ? ?0 cos( ?- ?0)= r2
极坐标方程分别是ρ=cosθ和ρ=sinθ的两个圆的圆心距是多少?
练 习 2
练习3
以极坐标系中的点(1,1)为圆心,1为半径的圆的方程是
C
3.极坐标方程
A.双曲线 B.椭圆 C.抛物线 D.圆
表示的曲线是( )
4.圆
的圆心坐标是( )
A. B. C. D.
B
B
小 结
a.在极坐标系中,点的极坐标是多值的,若点M在曲线C上,则点M的有些极坐标可能不适合曲线C的方程。
b. 圆的极坐标方程有多种形式,极坐标方程 可认为是圆的一般式方程。
(1)曲线的极坐标方程概念
(2)怎样求曲线的极坐标方程
( 3)圆的极坐标方程
极坐标方程与直角坐标方程可以相互转化,当研究对象与角和距离有关时,用极坐标方程解决比较方便,这是一个重要的解题技巧。在极坐标系中,当研究的问题用极坐标方程难以解决时,可转化为直角坐标方程求解。
